华师大版数学八年级下册 17.3.2一次函数的图象课件(共15张PPT)
文档属性
| 名称 | 华师大版数学八年级下册 17.3.2一次函数的图象课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 16:49:38 | ||
图片预览






文档简介
(共15张PPT)
2.一次函数的图象
一
学习目标
1.会画一次函数、正比例的图象.
2.理解一次函数的图象之间的位置关系.
3.了解一次函数y=kx+b(k≠0)中,k、b的几何意义.
二
重难点
重点:画一次函数、正比例函数的图像.
难点:了解一次函数y=kx+b(k≠0)中,k、b的几何意义.
1.知识回顾
三
教学过程
画函数图象的步骤是什么?
答:列表,描点,连线.
答:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.
平面直角坐标系中,x轴,y轴上的点的坐标有什么特征?
2.探究新知
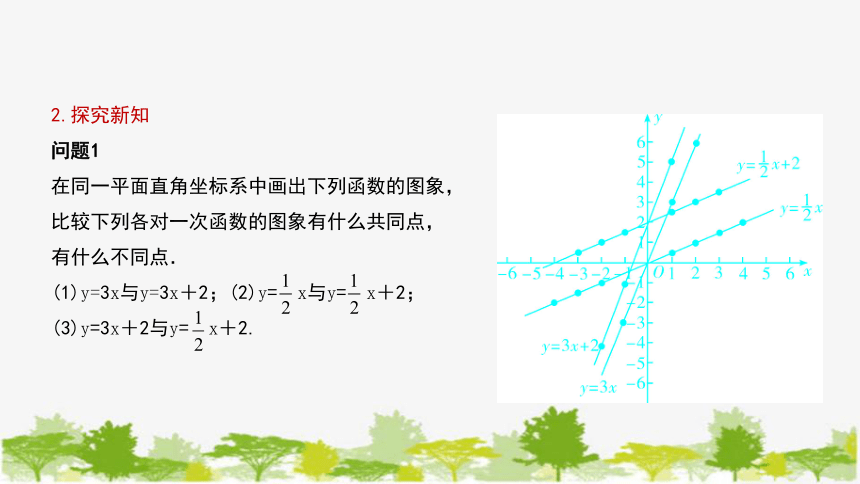
问题1
在同一平面直角坐标系中画出下列函数的图象,比较下列各对一次函数的图象有什么共同点,有什么不同点.
(1)y=3x与y=3x+2;(2)y= x与y= x+2;(3)y=3x+2与y= x+2.
解:如图所示.两个一次函数,当k一样,b不一样时,它们的函数图象是平行的,都是由直线y=kx(k≠0)向上或向下移动得到;而当两个一次函数b一样,k不一样时,它们的图象与y轴交于同一点(0,b),但这两条直线不平行.
问题2:
长方形的周长是8 cm,设一边长为x cm,另一边长为y cm.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在平面直角坐标系中画出此函数的图象,
解:(1)由题意,得2(x+y)=8,∴y=4-x.
∵ ∴0(2)图象如图所示:
【知识归纳】
(1)一次函数y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b.特别地,正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线.
(2)直线的基本事实:两点确定一条直线,所以画直线y=kx+b的快速方法是只需在直线上任意取两个点,画一条直线即可.
(3)联系统计图与实际问题的函数图象,说明两条坐标轴的取名及单位的规定可以有所变化,但必须明白在没有实际背景的函数图象中,两轴的单位长度一般应一致.
3.例题精讲
例1 分别在同一平面直角坐标系中画出下列函数的图象.
(1)y = 2x 与 y = 2x + 3;
(2)y = 2x + 1 与 y = x + 1.
解:(1)y=2x经过点(0,0)和点(1,2),过点(0,0)和点(1,2)作直线,就是所求直线y=2x;y=2x+3与x轴的交点为
(-1.5,3),与y轴的交点为(0,3),过点(-1.5,3)和点(0,3)作直线,就是
所求直线y=2x+3.如图所示.
(2)y=2x+1与x轴的交点为(-0.5,0),与y轴的交点为(0,1),过点(-0.5,0)和点(0,1)作直线,就是所求直线y=2x+1;y= x+1与x轴的交点为(-2,0),与y轴的交点为(0,1),过点(-2,0)和点(0,1)作直线,就是所求直线y= x+1.如图所示.
例2 求直线y = - 2x - 3 与x轴y轴的交点,并画出这条直线.
解:x轴上的点的纵坐标等于0,y轴上的点的横坐标等于0.交点同时在直线y =-2x-3 上,它的坐标(x,y)应满足 y =-2x-3 .于是,由y=0 可求得x=-1.5,点(-1.5,0)就是直线与X轴的交点;由x=0 可求得y=-3,点(0,-3)就是直线与y轴的交点;如图,过点(-1.5,0)和点(0,-3)作直线,就是所求直线 y =-2x-3 .
例3 汽车距北京的路程s(千米)与汽车在高速公路上行驶的时间t(时)之间的函数关系式是s = 570 - 95t,试画出这个函数的图象.
解:因为s>0,所以570-95t>0,t<6,又因为t>0,则自变量t的取值范围是0【分析】在实际问题中,我们可以在表示时间的t轴和表示路程的s轴上分别选取适当的单位长度,画出平面直角坐标系,如图所示.
4.巩固练习 完成教材课后同步练习
5.课堂小结
掌握画一次函数图象的画法.
2.一次函数的图象
一
学习目标
1.会画一次函数、正比例的图象.
2.理解一次函数的图象之间的位置关系.
3.了解一次函数y=kx+b(k≠0)中,k、b的几何意义.
二
重难点
重点:画一次函数、正比例函数的图像.
难点:了解一次函数y=kx+b(k≠0)中,k、b的几何意义.
1.知识回顾
三
教学过程
画函数图象的步骤是什么?
答:列表,描点,连线.
答:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.
平面直角坐标系中,x轴,y轴上的点的坐标有什么特征?
2.探究新知
问题1
在同一平面直角坐标系中画出下列函数的图象,比较下列各对一次函数的图象有什么共同点,有什么不同点.
(1)y=3x与y=3x+2;(2)y= x与y= x+2;(3)y=3x+2与y= x+2.
解:如图所示.两个一次函数,当k一样,b不一样时,它们的函数图象是平行的,都是由直线y=kx(k≠0)向上或向下移动得到;而当两个一次函数b一样,k不一样时,它们的图象与y轴交于同一点(0,b),但这两条直线不平行.
问题2:
长方形的周长是8 cm,设一边长为x cm,另一边长为y cm.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)在平面直角坐标系中画出此函数的图象,
解:(1)由题意,得2(x+y)=8,∴y=4-x.
∵ ∴0
【知识归纳】
(1)一次函数y=kx+b(k≠0)的图象是一条直线.通常也称为直线y=kx+b.特别地,正比例函数y=kx(k≠0)的图象是经过原点(0,0)的一条直线.
(2)直线的基本事实:两点确定一条直线,所以画直线y=kx+b的快速方法是只需在直线上任意取两个点,画一条直线即可.
(3)联系统计图与实际问题的函数图象,说明两条坐标轴的取名及单位的规定可以有所变化,但必须明白在没有实际背景的函数图象中,两轴的单位长度一般应一致.
3.例题精讲
例1 分别在同一平面直角坐标系中画出下列函数的图象.
(1)y = 2x 与 y = 2x + 3;
(2)y = 2x + 1 与 y = x + 1.
解:(1)y=2x经过点(0,0)和点(1,2),过点(0,0)和点(1,2)作直线,就是所求直线y=2x;y=2x+3与x轴的交点为
(-1.5,3),与y轴的交点为(0,3),过点(-1.5,3)和点(0,3)作直线,就是
所求直线y=2x+3.如图所示.
(2)y=2x+1与x轴的交点为(-0.5,0),与y轴的交点为(0,1),过点(-0.5,0)和点(0,1)作直线,就是所求直线y=2x+1;y= x+1与x轴的交点为(-2,0),与y轴的交点为(0,1),过点(-2,0)和点(0,1)作直线,就是所求直线y= x+1.如图所示.
例2 求直线y = - 2x - 3 与x轴y轴的交点,并画出这条直线.
解:x轴上的点的纵坐标等于0,y轴上的点的横坐标等于0.交点同时在直线y =-2x-3 上,它的坐标(x,y)应满足 y =-2x-3 .于是,由y=0 可求得x=-1.5,点(-1.5,0)就是直线与X轴的交点;由x=0 可求得y=-3,点(0,-3)就是直线与y轴的交点;如图,过点(-1.5,0)和点(0,-3)作直线,就是所求直线 y =-2x-3 .
例3 汽车距北京的路程s(千米)与汽车在高速公路上行驶的时间t(时)之间的函数关系式是s = 570 - 95t,试画出这个函数的图象.
解:因为s>0,所以570-95t>0,t<6,又因为t>0,则自变量t的取值范围是0
4.巩固练习 完成教材课后同步练习
5.课堂小结
掌握画一次函数图象的画法.
