同底数幂的乘法[下学期]
文档属性
| 名称 | 同底数幂的乘法[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-13 19:34:00 | ||
图片预览








文档简介
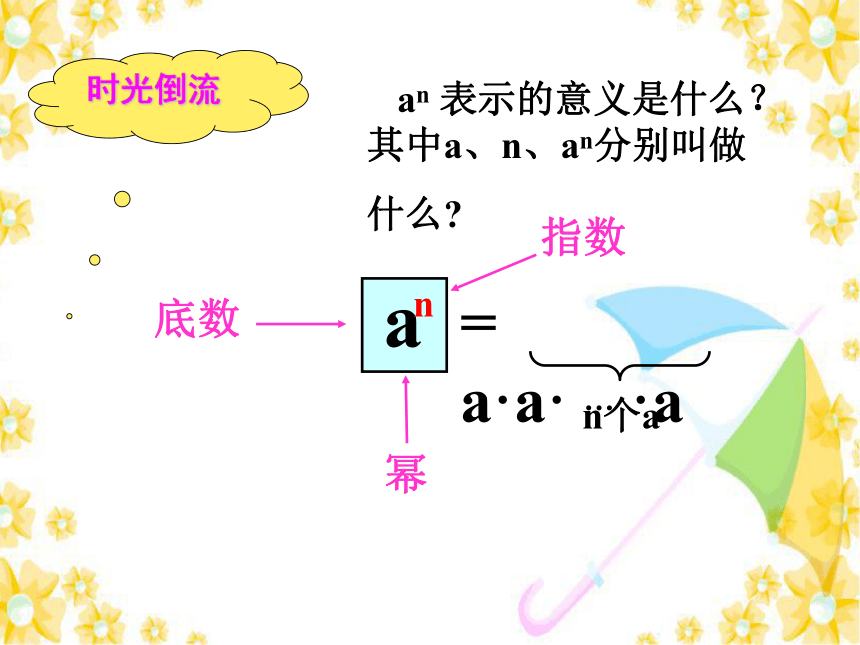
课件21张PPT。南马镇中:陈晓安同底数幂的乘法102 × 105 × 10 7 等于多少呢?3×105× 3×107= 1.44×102×105 × 107 16×(千米)指数幂底数an 表示的意义是什么?其中a、n、an分别叫做
什么?
时光倒流合作学习 23×22 = ( ) ×( )
=________________=2( ) =2( )+( )(2)102×105 = ( ) ×( )
=_______________________________
=10( ) =10( )+( )(3) a4 · a3 = ( ) · ( )
=_________ =a( ) =a( )+( )2 × 2 × 22 × 22 × 2 × 2 × 2 × 253210×1010 × 10 × 10 × 10 × 1010 × 10 × 10 × 10 × 10 × 10 × 10725aaaaaaaaaaaaaa743请同学们根据自己的理解,完成下列填空
思考:观察上面各题左右两边,底数、指数有什么关系?
猜一猜:猜想: am · an = (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a 同底数幂相乘,底数不变,指数相加
即 am · an = am+n (m、n都是正整数)(aa…a)(aa…a)am+n?同底数幂的乘法法则:对运算性质的剖析: 条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加例1 计算下列各式,结果用幂的形式表示 (1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 (3) x3 · x5 (4) (a-b)2 (a-b)学以致用我喜欢数学让我来当数学老师每组编一道同底数幂的乘法的题目,(要求自己首先应该会做)看谁编地又快又好!
下面的计算有毛病吗?如果有,请改正!
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 (-7)8 · 73 = 711 a · a6 = a7× × × ×××? 数学医院 ? (3)x2 ·x3 = x6 ( ) (4)(-7)8 · 7 3 = (-7)11 ( )(5)a · a6 = a6 ( ) (6)m + m3 = m4 ( ) 小医生的温馨提示:通过上面的练习你认为同底数幂的乘法
法则的应用应注意什么?1.同底数幂相乘时,指数是相加的
2.注意 am · an 与am + an的区别
3.不能疏忽指数为1的情况
我国自行研制的“神威 I”计算机的峰值运算速度达到每秒 3840亿次.如果按这个速度工作一整天,那么它能运算多少次? (结果保留3个有效数字)?解: 3840 亿次 = 3.84 ×103 × 108 次,
24时 = 24 × 3.6 × 103 秒答:它一天约能运算3.32 × 1016次
(乘法的交换律和结合律)= (3.84 × 24 × 3.6) ×(103 × 108 × 103 )= 331.776 × 1014 ≈ 3.32 × 1016(次)(3.84 × 103 × 108) ×( 24 × 3.6 × 103 )生活中的数学am · an · ap 等于什么?猜想:举一反三运用同底数幂的乘法法则计算下
列各式,并用幂的形式表示结果: 2 7 × 23 (2) (-3) 4 × (-3)7
(3) (-5) 2 × (-5)3 × 54 (4) (x+y) 3× (x+y)解: (1) 2 7 × 23 = 27+3 = 210 (2) (-3) 4 × (-3)7 = (-3) 4+7 = (-3)11
(3) (-5) 2 × (-5)3 × 54 = (-5) 2+3+4 =(-5)9 (4) (x+y) 3× (x+y)= (x+y) 3+1= (x+y)4脑筋快快快挑战自我,超越梦想:挑战 :1挑战自我,超越梦想:挑战 :2挑战自我,超越梦想挑战 :3课堂小结同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:注意:同底数幂相乘时通过本节课的学习,你在知识上有哪些收获,你学到了哪些方法?四、提炼小结 完善结构
布置作业1.必做题: 课本第104页 A 组
作业本第22页
2.选做题:课本第104页 B 组
什么?
时光倒流合作学习 23×22 = ( ) ×( )
=________________=2( ) =2( )+( )(2)102×105 = ( ) ×( )
=_______________________________
=10( ) =10( )+( )(3) a4 · a3 = ( ) · ( )
=_________ =a( ) =a( )+( )2 × 2 × 22 × 22 × 2 × 2 × 2 × 253210×1010 × 10 × 10 × 10 × 1010 × 10 × 10 × 10 × 10 × 10 × 10725aaaaaaaaaaaaaa743请同学们根据自己的理解,完成下列填空
思考:观察上面各题左右两边,底数、指数有什么关系?
猜一猜:猜想: am · an = (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a 同底数幂相乘,底数不变,指数相加
即 am · an = am+n (m、n都是正整数)(aa…a)(aa…a)am+n?同底数幂的乘法法则:对运算性质的剖析: 条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加例1 计算下列各式,结果用幂的形式表示 (1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 (3) x3 · x5 (4) (a-b)2 (a-b)学以致用我喜欢数学让我来当数学老师每组编一道同底数幂的乘法的题目,(要求自己首先应该会做)看谁编地又快又好!
下面的计算有毛病吗?如果有,请改正!
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 (-7)8 · 73 = 711 a · a6 = a7× × × ×××? 数学医院 ? (3)x2 ·x3 = x6 ( ) (4)(-7)8 · 7 3 = (-7)11 ( )(5)a · a6 = a6 ( ) (6)m + m3 = m4 ( ) 小医生的温馨提示:通过上面的练习你认为同底数幂的乘法
法则的应用应注意什么?1.同底数幂相乘时,指数是相加的
2.注意 am · an 与am + an的区别
3.不能疏忽指数为1的情况
我国自行研制的“神威 I”计算机的峰值运算速度达到每秒 3840亿次.如果按这个速度工作一整天,那么它能运算多少次? (结果保留3个有效数字)?解: 3840 亿次 = 3.84 ×103 × 108 次,
24时 = 24 × 3.6 × 103 秒答:它一天约能运算3.32 × 1016次
(乘法的交换律和结合律)= (3.84 × 24 × 3.6) ×(103 × 108 × 103 )= 331.776 × 1014 ≈ 3.32 × 1016(次)(3.84 × 103 × 108) ×( 24 × 3.6 × 103 )生活中的数学am · an · ap 等于什么?猜想:举一反三运用同底数幂的乘法法则计算下
列各式,并用幂的形式表示结果: 2 7 × 23 (2) (-3) 4 × (-3)7
(3) (-5) 2 × (-5)3 × 54 (4) (x+y) 3× (x+y)解: (1) 2 7 × 23 = 27+3 = 210 (2) (-3) 4 × (-3)7 = (-3) 4+7 = (-3)11
(3) (-5) 2 × (-5)3 × 54 = (-5) 2+3+4 =(-5)9 (4) (x+y) 3× (x+y)= (x+y) 3+1= (x+y)4脑筋快快快挑战自我,超越梦想:挑战 :1挑战自我,超越梦想:挑战 :2挑战自我,超越梦想挑战 :3课堂小结同底数幂的乘法性质:底数 ,指数 .不变相加幂的意义:注意:同底数幂相乘时通过本节课的学习,你在知识上有哪些收获,你学到了哪些方法?四、提炼小结 完善结构
布置作业1.必做题: 课本第104页 A 组
作业本第22页
2.选做题:课本第104页 B 组
