1.6反冲现象火箭 课件 (共24张PPT)
文档属性
| 名称 | 1.6反冲现象火箭 课件 (共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 32.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-01 09:27:45 | ||
图片预览






文档简介
(共24张PPT)
第一章 动量守恒定律
1.6 反冲现象 火箭
一、反冲现象
把气球吹满气,然后松手,气球会怎样?
发射炮弹时,炮弹从炮筒中飞出,炮身向后运动。
用枪射击时, 子弹向前飞去,枪身向后运动。
一、反冲现象
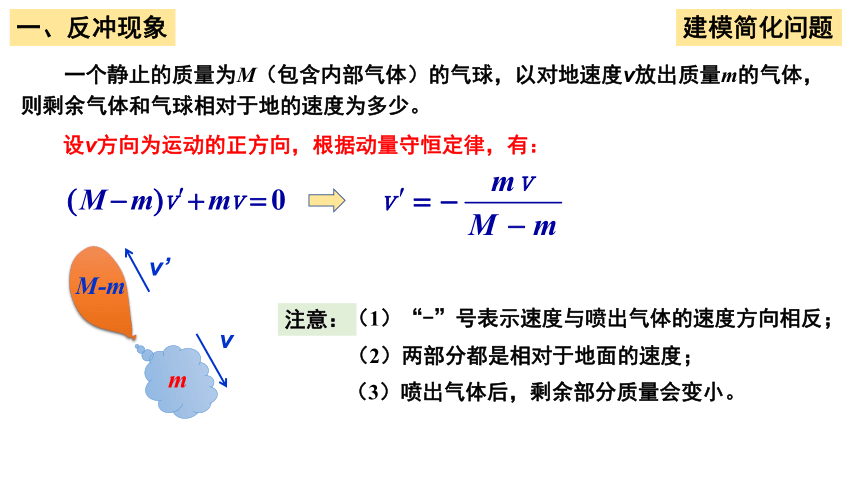
(1)“-”号表示速度与喷出气体的速度方向相反;
一个静止的质量为M(包含内部气体)的气球,以对地速度v放出质量m的气体,则剩余气体和气球相对于地的速度为多少。
设v方向为运动的正方向,根据动量守恒定律,有:
v’
v
M-m
m
建模简化问题
注意:
(2)两部分都是相对于地面的速度;
(3)喷出气体后,剩余部分质量会变小。
一、反冲现象
反冲小车
用酒精灯加热试管中的水
一、反冲现象
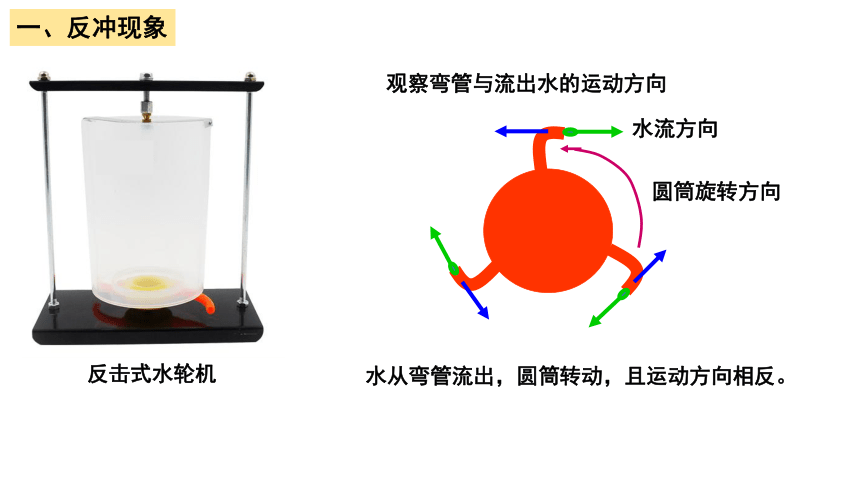
反击式水轮机
一、反冲现象
水从弯管流出,圆筒转动,且运动方向相反。
观察弯管与流出水的运动方向
水流方向
圆筒旋转方向
反击式水轮机
一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
2. 条件:
(1)一个静止(初动量为零)的物体分为两部分;
(2)两部分运动方向必然相对相反;
(3)在内力的作用下。
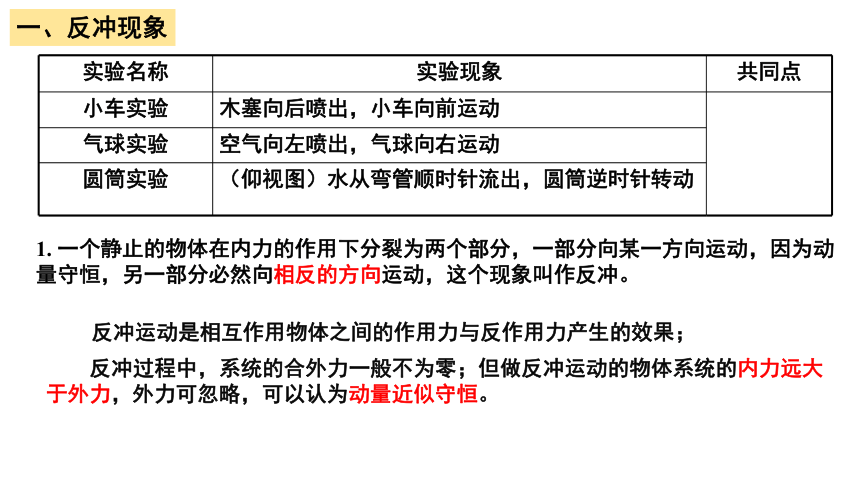
实验名称 实验现象 共同点
小车实验 木塞向后喷出,小车向前运动
气球实验 空气向左喷出,气球向右运动 圆筒实验 (仰视图)水从弯管顺时针流出,圆筒逆时针转动 一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
实验名称 实验现象 共同点
小车实验 木塞向后喷出,小车向前运动
气球实验 空气向左喷出,气球向右运动 圆筒实验 (仰视图)水从弯管顺时针流出,圆筒逆时针转动 反冲运动是相互作用物体之间的作用力与反作用力产生的效果;
反冲过程中,系统的合外力一般不为零;但做反冲运动的物体系统的内力远大于外力,外力可忽略,可以认为动量近似守恒。
一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
2. 反冲运动的特点:
(1)系统内力远远大于外力,系统动量守恒;
3. 反冲运动的原理
P' = P 即 m1v1 + m2v2 = 0 故有:
负号就表示作用后的两部分运动方向相反
(2)有其他形式的能转化为动能,系统动能增加。
冲天炮飞上天
水母向前运动
一、反冲现象
喷水飞鞋
喷灌装置
实际生产、生活中应用反冲现象的例子也很多,例如农田、园林的喷灌装置能够一边喷水一边旋转,这是因为喷口的朝向略有偏斜,水从喷口喷出时,喷管因反冲而旋转。这样可以自动改变喷水的方向。
一、反冲现象
应用
榴弹炮
止退犁
(火炮缓冲器)
一、反冲现象
防止
火 箭
喷气式飞机
一、反冲现象
古代火箭
构造和原理:箭杆上捆一个前端封闭的火药筒,点燃后成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
二、火箭
箭身
火药筒
喷气方向
我国早在宋代就发明了火箭,箭杆上捆一个前端封闭的火药筒,点燃后生成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
喷气式飞机和火箭的飞行应用了反冲的原理,它们都是靠喷出气流的反冲作用而获得巨大速度的。
二、火箭
通过喷射高温高压燃气而获得反作用力,从而沿燃气喷射的反方向飞行。
火箭工作原理:
现代火箭
例:火箭发射前的总质量为M、燃料燃尽后的质量为m,火箭燃气的喷射速度为v1,求燃料燃尽后火箭的飞行速度v为多大?
空气阻力、重力
二、火箭
1. 影响火箭速度的主要因素:
(1)燃气喷射的速度
解:火箭发射过程中内力远大于外力,所以动量守恒。(以火箭的速度方向为正方向)
则: mv -(M-m)v1= 0
(2)火箭的质量比(即火箭开始飞行时的质量与燃料燃尽时的质量之比)目前的技术条件下,火箭的质量比在6-10左右。
二、火箭
要提高喷气速度,需要使用高质量的燃料:
液氢——燃料
液氧——氧化剂
1. 如何提高喷气速度?
2. 如何提高质量比?
主要结构:
飞船
第二级火箭
第一级火箭
火箭发射过程:
第一级火箭点燃
燃尽,空壳脱落
下一级火箭点燃
多级火箭能及时把空壳抛掉,使火箭的总质量减少,因而能够达到很高的速度,但火箭的级数不是越多越好,级数越多构造越复杂,工作的可靠性越差,目前多级火箭一般都是三级。
二、火箭
一火箭喷气发动机每次喷出m=200 g的气体,气体离开发动机时速度v=1000 m/s,设火箭质量M=300 kg,发动机每秒喷气20次,求:
(1)当第3次气体喷出后,火箭的速度多大?
(2)运动第1s末,火箭的速度多大?
(1)设喷出3次气体后火箭的速度为v3,以火箭和喷出的3次气体为研究对象,根据动量守恒定律可得:
(M-3m)v3-3mv=0
(2)以火箭和喷出的20次气体为研究对象,根据动量守恒可得:
(M-20m)v20-20mv=0
由于每次喷气速度都一样,可选整体为研究对象,运用动量守恒来求解:
二、火箭
三、人船
男生向右,船向左
女生向左,船向右
解决实际问题
如何悄无声息的测出女生的体重?
三、人船
v1
v2
人和船组成的系统,在人从船头走向船尾的过程中,水平方向上动量守恒。
以向左为正,由动量守恒定律可得:
S2
S1
设人和船相对地面的位移分别为S1和S2:
则:
解得:
如果人是变速运动呢?
三、人船
由图可得:
一个质量为M,底面边长为 b 的斜面静止在光滑的水平地面上,有一质量为 m 的物块由斜面顶部无初速滑到底部时,斜面移动的距离是多少?
M
m
三、人船
S1
S2
b
M
m
由上图看出:s1 + s2 = b
分析和解答:劈和小球组成的系统水平方向不受外力,故水平方向动量守恒,且初始时两物均静止,故由推论知:
ms1=Ms2
处理此类题,关键是画草图,确定位移关系。
三、人船
代入上式得:m(b-s2)=Ms2
所以: s2=mb/(M+m)
第一章 动量守恒定律
1.6 反冲现象 火箭
一、反冲现象
把气球吹满气,然后松手,气球会怎样?
发射炮弹时,炮弹从炮筒中飞出,炮身向后运动。
用枪射击时, 子弹向前飞去,枪身向后运动。
一、反冲现象
(1)“-”号表示速度与喷出气体的速度方向相反;
一个静止的质量为M(包含内部气体)的气球,以对地速度v放出质量m的气体,则剩余气体和气球相对于地的速度为多少。
设v方向为运动的正方向,根据动量守恒定律,有:
v’
v
M-m
m
建模简化问题
注意:
(2)两部分都是相对于地面的速度;
(3)喷出气体后,剩余部分质量会变小。
一、反冲现象
反冲小车
用酒精灯加热试管中的水
一、反冲现象
反击式水轮机
一、反冲现象
水从弯管流出,圆筒转动,且运动方向相反。
观察弯管与流出水的运动方向
水流方向
圆筒旋转方向
反击式水轮机
一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
2. 条件:
(1)一个静止(初动量为零)的物体分为两部分;
(2)两部分运动方向必然相对相反;
(3)在内力的作用下。
实验名称 实验现象 共同点
小车实验 木塞向后喷出,小车向前运动
气球实验 空气向左喷出,气球向右运动 圆筒实验 (仰视图)水从弯管顺时针流出,圆筒逆时针转动 一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
实验名称 实验现象 共同点
小车实验 木塞向后喷出,小车向前运动
气球实验 空气向左喷出,气球向右运动 圆筒实验 (仰视图)水从弯管顺时针流出,圆筒逆时针转动 反冲运动是相互作用物体之间的作用力与反作用力产生的效果;
反冲过程中,系统的合外力一般不为零;但做反冲运动的物体系统的内力远大于外力,外力可忽略,可以认为动量近似守恒。
一、反冲现象
1. 一个静止的物体在内力的作用下分裂为两个部分,一部分向某一方向运动,因为动量守恒,另一部分必然向相反的方向运动,这个现象叫作反冲。
2. 反冲运动的特点:
(1)系统内力远远大于外力,系统动量守恒;
3. 反冲运动的原理
P' = P 即 m1v1 + m2v2 = 0 故有:
负号就表示作用后的两部分运动方向相反
(2)有其他形式的能转化为动能,系统动能增加。
冲天炮飞上天
水母向前运动
一、反冲现象
喷水飞鞋
喷灌装置
实际生产、生活中应用反冲现象的例子也很多,例如农田、园林的喷灌装置能够一边喷水一边旋转,这是因为喷口的朝向略有偏斜,水从喷口喷出时,喷管因反冲而旋转。这样可以自动改变喷水的方向。
一、反冲现象
应用
榴弹炮
止退犁
(火炮缓冲器)
一、反冲现象
防止
火 箭
喷气式飞机
一、反冲现象
古代火箭
构造和原理:箭杆上捆一个前端封闭的火药筒,点燃后成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
二、火箭
箭身
火药筒
喷气方向
我国早在宋代就发明了火箭,箭杆上捆一个前端封闭的火药筒,点燃后生成的燃气以很大速度向后喷出,箭杆由于反冲而向前运动。
喷气式飞机和火箭的飞行应用了反冲的原理,它们都是靠喷出气流的反冲作用而获得巨大速度的。
二、火箭
通过喷射高温高压燃气而获得反作用力,从而沿燃气喷射的反方向飞行。
火箭工作原理:
现代火箭
例:火箭发射前的总质量为M、燃料燃尽后的质量为m,火箭燃气的喷射速度为v1,求燃料燃尽后火箭的飞行速度v为多大?
空气阻力、重力
二、火箭
1. 影响火箭速度的主要因素:
(1)燃气喷射的速度
解:火箭发射过程中内力远大于外力,所以动量守恒。(以火箭的速度方向为正方向)
则: mv -(M-m)v1= 0
(2)火箭的质量比(即火箭开始飞行时的质量与燃料燃尽时的质量之比)目前的技术条件下,火箭的质量比在6-10左右。
二、火箭
要提高喷气速度,需要使用高质量的燃料:
液氢——燃料
液氧——氧化剂
1. 如何提高喷气速度?
2. 如何提高质量比?
主要结构:
飞船
第二级火箭
第一级火箭
火箭发射过程:
第一级火箭点燃
燃尽,空壳脱落
下一级火箭点燃
多级火箭能及时把空壳抛掉,使火箭的总质量减少,因而能够达到很高的速度,但火箭的级数不是越多越好,级数越多构造越复杂,工作的可靠性越差,目前多级火箭一般都是三级。
二、火箭
一火箭喷气发动机每次喷出m=200 g的气体,气体离开发动机时速度v=1000 m/s,设火箭质量M=300 kg,发动机每秒喷气20次,求:
(1)当第3次气体喷出后,火箭的速度多大?
(2)运动第1s末,火箭的速度多大?
(1)设喷出3次气体后火箭的速度为v3,以火箭和喷出的3次气体为研究对象,根据动量守恒定律可得:
(M-3m)v3-3mv=0
(2)以火箭和喷出的20次气体为研究对象,根据动量守恒可得:
(M-20m)v20-20mv=0
由于每次喷气速度都一样,可选整体为研究对象,运用动量守恒来求解:
二、火箭
三、人船
男生向右,船向左
女生向左,船向右
解决实际问题
如何悄无声息的测出女生的体重?
三、人船
v1
v2
人和船组成的系统,在人从船头走向船尾的过程中,水平方向上动量守恒。
以向左为正,由动量守恒定律可得:
S2
S1
设人和船相对地面的位移分别为S1和S2:
则:
解得:
如果人是变速运动呢?
三、人船
由图可得:
一个质量为M,底面边长为 b 的斜面静止在光滑的水平地面上,有一质量为 m 的物块由斜面顶部无初速滑到底部时,斜面移动的距离是多少?
M
m
三、人船
S1
S2
b
M
m
由上图看出:s1 + s2 = b
分析和解答:劈和小球组成的系统水平方向不受外力,故水平方向动量守恒,且初始时两物均静止,故由推论知:
ms1=Ms2
处理此类题,关键是画草图,确定位移关系。
三、人船
代入上式得:m(b-s2)=Ms2
所以: s2=mb/(M+m)
