圆内接四边形[下学期]
图片预览


文档简介
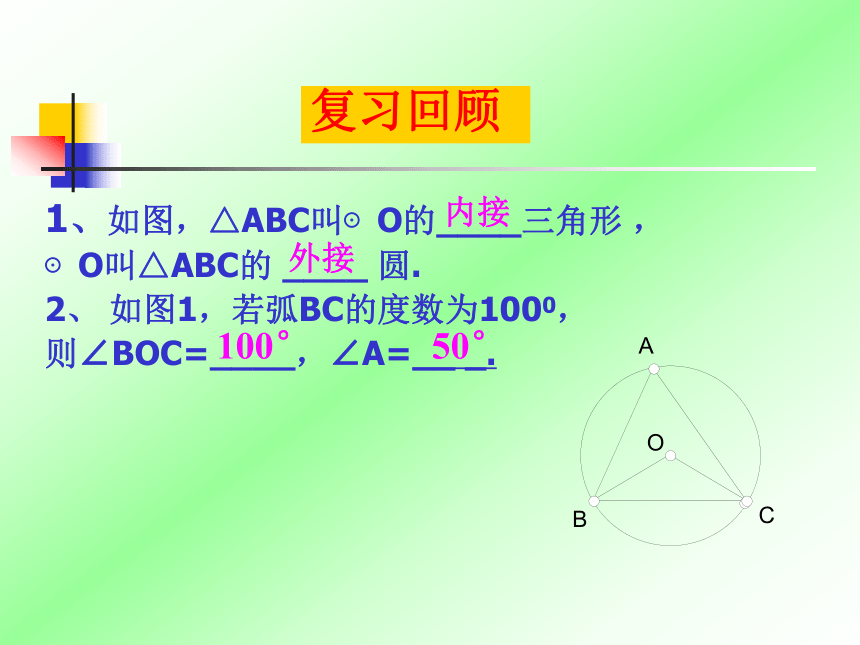
课件17张PPT。圆的内接四边形1、如图,△ABC叫⊙O的____三角形 ,
⊙O叫△ABC的 ____ 圆.
2、 如图1,若弧BC的度数为1000,
则∠BOC=____,∠A=__ _.
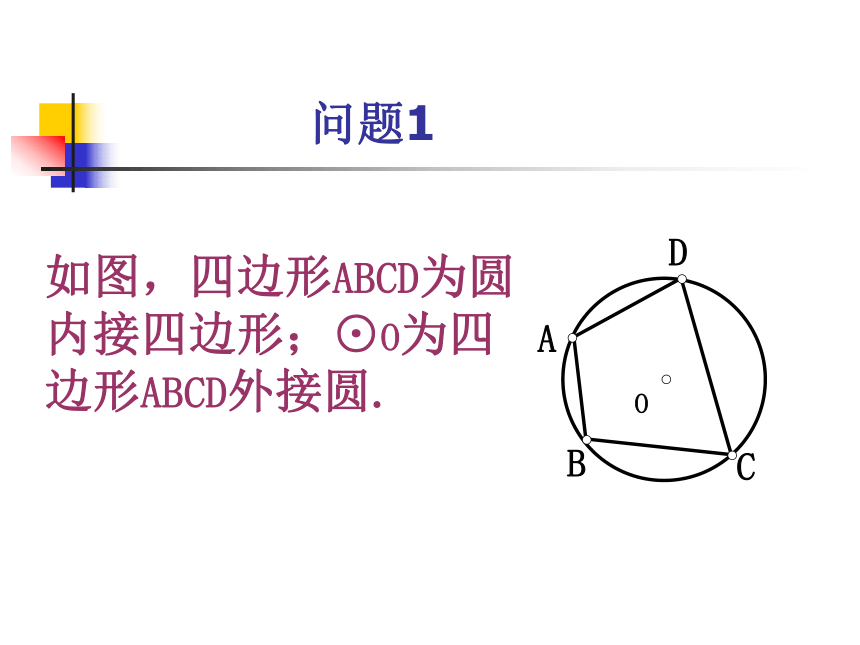
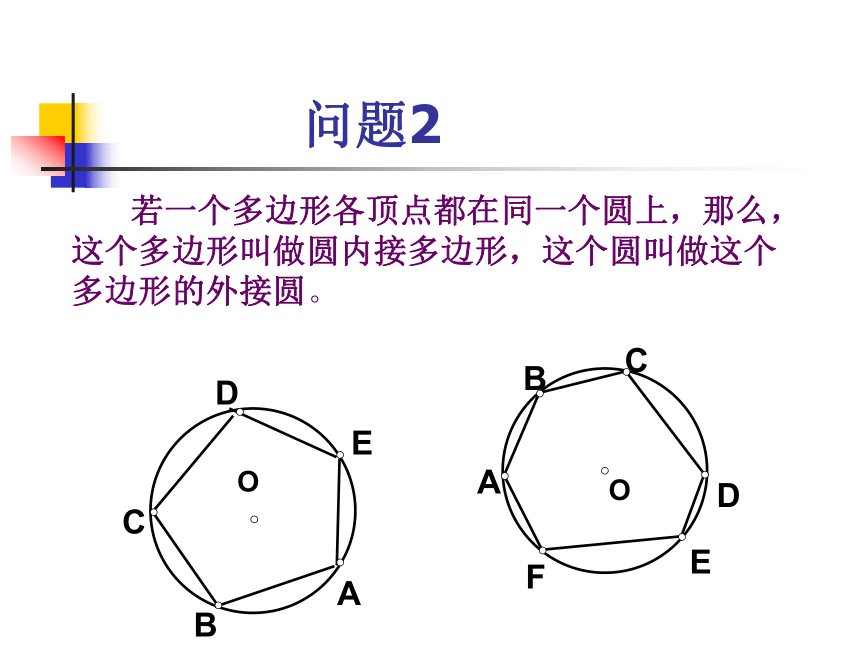
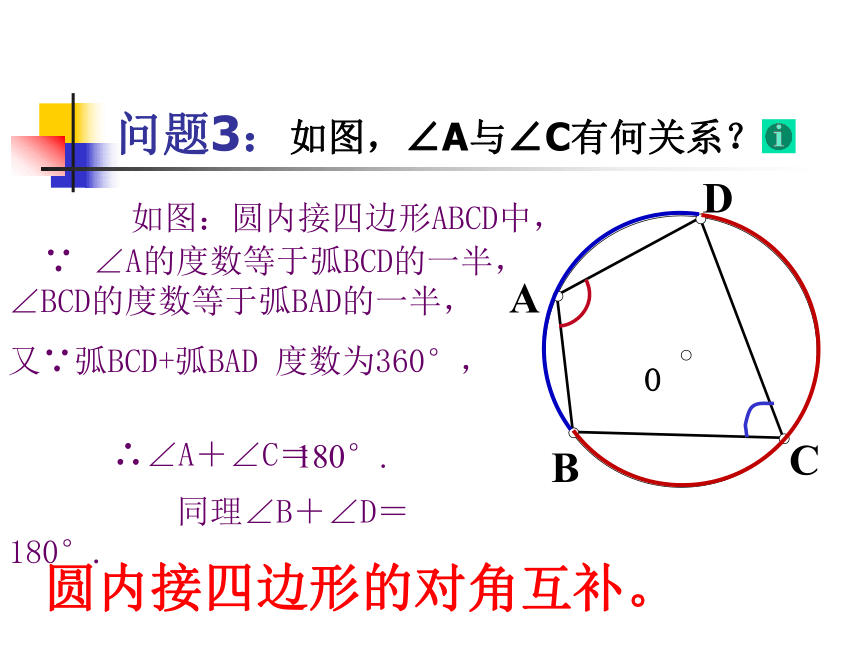
复习回顾 内接 外接 100° 50° 教学目标C 运用圆内接四边形的性质解决有关问题;A 识记圆的内接四边形的概念;B 掌握圆内接四边形的性质;如图,四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆. 问题1 若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OACDEB问题2CODBA 如图:圆内接四边形ABCD中, ∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
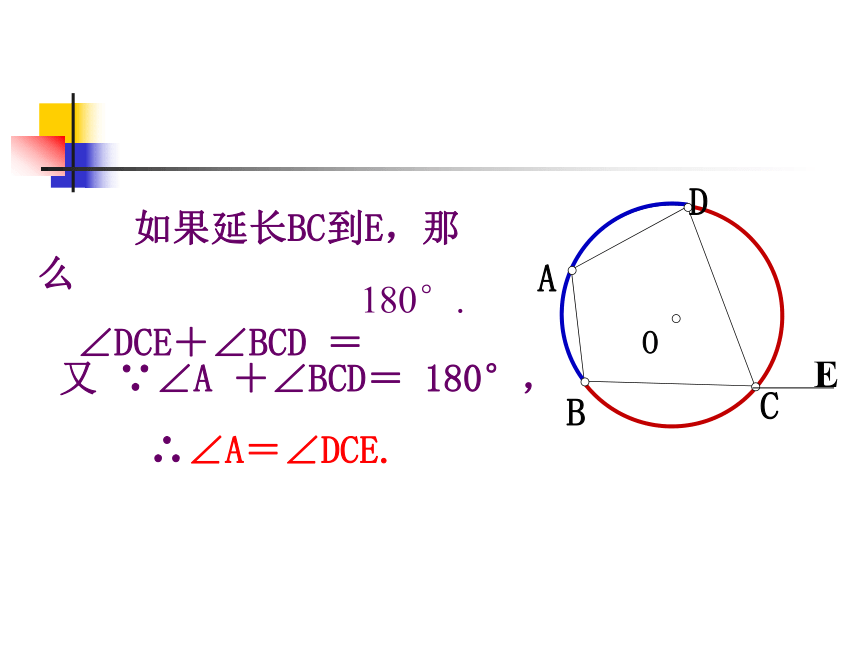
又∵弧BCD+弧BAD 度数为360°, ∴∠A+∠C=180°. 同理∠B+∠D=180°.圆内接四边形的对角互补。 问题3:如图,∠A与∠C有何关系? 如果延长BC到E,那么
∠DCE+∠BCD =180°. ∴∠A=∠DCE.又 ∵∠A +∠BCD= 180°,因为∠A是与∠DCE相邻的
内角∠DCB的对角,我们把
∠A叫做∠DCE的内对角。圆内接四边形的一个
外角等于它的内对角。∠A=∠DCE 探索结论 先根据图形讨论,然后用语言归纳为 :圆的内接四边形的对角互补,并且任何一个外角
都等于它的内对角。 几何表达式:
∵ 四边形ABCD内接于⊙O,
∴ ∠A+∠C=180°且∠B=∠1 .性质定理:应用举例例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。
求证:CE∥DF
CE∥DF ∠E+∠F=180° ∠E+∠1=180°、∠1=∠F连结AB1 思路分析 证明:连结AB 例1: 如图4,⊙O1和⊙O2都经过A、B两点, 经过点A的直线CD
与⊙O1相交于点C,与⊙O2相交于点D,经过点B的直线EF与⊙O1
相交于点E,与⊙O2相交于点F。
求证:CE∥DF ∵ABEC是⊙O1的内接四边形 ∴∠1+∠E =1800 又∵ADFB是⊙O2的内接四边形 ∴∠1=∠F. ∴∠E+∠F=1800 ∴CE∥DF 1反思与拓展 证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果? 1)延长EF,是否有∠E=∠BAD= ∠1 ?
2) 延长DF, 能否证明∠E=∠2=∠3? 一、填空: (1)四边形ABCD内接于⊙O,则∠A+∠C=__ ,∠B+∠ADC=_____;若∠B=800, 则∠ADC=______ ∠CDE=______(图1) (2)四边形ABCD内接于⊙O,∠AOC=1000 则∠B=______∠D=______(图2) 图1 (3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____, 180° 180° 100° 80°
?
50° 130° 45° 达标练习 图2(4)如图3,梯形ABCD内接于⊙O,AD∥BC, ∠B=750,
则∠C=_____.
2、选择题: (5)圆内接平行四边形必为( ) A.菱形 B.矩形 C.正方形 D.等腰梯形
75° B 返回 图3课堂小结 本节课所学的内容可概括为三个“1”.一个概念:圆的内接四边形;一个定理:圆的内接四边形的性质定理;添辅助线的方法:作两圆的公共弦. 课外作业复习巩固所学的知识内容;
完成课本习题7.2 A组16、17题;
思考题:过任意四点能不能作圆?
⊙O叫△ABC的 ____ 圆.
2、 如图1,若弧BC的度数为1000,
则∠BOC=____,∠A=__ _.
复习回顾 内接 外接 100° 50° 教学目标C 运用圆内接四边形的性质解决有关问题;A 识记圆的内接四边形的概念;B 掌握圆内接四边形的性质;如图,四边形ABCD为圆内接四边形;⊙O为四边形ABCD外接圆. 问题1 若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OACDEB问题2CODBA 如图:圆内接四边形ABCD中, ∵ ∠A的度数等于弧BCD的一半,∠BCD的度数等于弧BAD的一半,
又∵弧BCD+弧BAD 度数为360°, ∴∠A+∠C=180°. 同理∠B+∠D=180°.圆内接四边形的对角互补。 问题3:如图,∠A与∠C有何关系? 如果延长BC到E,那么
∠DCE+∠BCD =180°. ∴∠A=∠DCE.又 ∵∠A +∠BCD= 180°,因为∠A是与∠DCE相邻的
内角∠DCB的对角,我们把
∠A叫做∠DCE的内对角。圆内接四边形的一个
外角等于它的内对角。∠A=∠DCE 探索结论 先根据图形讨论,然后用语言归纳为 :圆的内接四边形的对角互补,并且任何一个外角
都等于它的内对角。 几何表达式:
∵ 四边形ABCD内接于⊙O,
∴ ∠A+∠C=180°且∠B=∠1 .性质定理:应用举例例 如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1 交于点C,与⊙O2 交于点D。经过点B的直线EF与⊙O1 交于点E,与⊙O2 交于点F。
求证:CE∥DF
CE∥DF ∠E+∠F=180° ∠E+∠1=180°、∠1=∠F连结AB1 思路分析 证明:连结AB 例1: 如图4,⊙O1和⊙O2都经过A、B两点, 经过点A的直线CD
与⊙O1相交于点C,与⊙O2相交于点D,经过点B的直线EF与⊙O1
相交于点E,与⊙O2相交于点F。
求证:CE∥DF ∵ABEC是⊙O1的内接四边形 ∴∠1+∠E =1800 又∵ADFB是⊙O2的内接四边形 ∴∠1=∠F. ∴∠E+∠F=1800 ∴CE∥DF 1反思与拓展 证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE ∥ DF,想一想还能否通过同位角相等或者内错角相等证明结果? 1)延长EF,是否有∠E=∠BAD= ∠1 ?
2) 延长DF, 能否证明∠E=∠2=∠3? 一、填空: (1)四边形ABCD内接于⊙O,则∠A+∠C=__ ,∠B+∠ADC=_____;若∠B=800, 则∠ADC=______ ∠CDE=______(图1) (2)四边形ABCD内接于⊙O,∠AOC=1000 则∠B=______∠D=______(图2) 图1 (3)四边形ABCD内接于⊙O, ∠A:∠C=1:3,则∠A=_____, 180° 180° 100° 80°
?
50° 130° 45° 达标练习 图2(4)如图3,梯形ABCD内接于⊙O,AD∥BC, ∠B=750,
则∠C=_____.
2、选择题: (5)圆内接平行四边形必为( ) A.菱形 B.矩形 C.正方形 D.等腰梯形
75° B 返回 图3课堂小结 本节课所学的内容可概括为三个“1”.一个概念:圆的内接四边形;一个定理:圆的内接四边形的性质定理;添辅助线的方法:作两圆的公共弦. 课外作业复习巩固所学的知识内容;
完成课本习题7.2 A组16、17题;
思考题:过任意四点能不能作圆?
