三线八角[下学期]
图片预览


文档简介
【教学题目】三线八角
【教学目标】
知识与技能
1.使学生理解三线八角的意义,并能从复杂图形中识别它们.
2.通过三线八角的特点的分析,培养学生抽象概括问题的能力.
3.使学生认识图形是由简到繁组合而成,培养学生形成基本图形结构的能力.
过程与方法
通过学生探索三条直线的位置关系引入三线八角的概念,在学生探索的过程中加深学生对概念的理解,通过具体的例题使学生掌握在复杂图形中识别三线八角的方法。
情感态度与价值观
培养学生的探索归纳能力
【教学重点】
三线八角的意义
【教学难点】
能在各种变式的图形中找出这三类角
【教学过程】
复习提问
前面我们学习了相交线,两条直线相交后产生了几个角?每两个角之间的关系是什么?
(除平角外,产生四个角,对顶角相等,邻补角互补)
引入新课
三条直线之间可以有什么样的位置关系?(请你用三支笔表示三条直线,来排放一下可能存在的位置关系。)
(1)三条直线都平行(没有交点).
(2)两条直线平行被第三条直线所截(两个交点).
(3)三条直线两两相交(有三个交点).
(4)三条直线交于一点(一个交点).
前面我们对相交的两条直线所形成的四个角进行研究,今天我们就对三条直线相交后形成的八个角如图2-30(3)进行研究,简称为:三线八角.(板书课题)
新课讲解
在图2-31中,l1和l3(或l2和l3)所形成的四个角是有公共顶点的,而每两个角之间的关系从位置来分,可分为两类:对顶角和邻补角,而上面四个角和下面四个角是没有公共顶点的,那么上面的一个与下面的一个又有什么样的位置关系呢?这就是下面所要研究的问题.
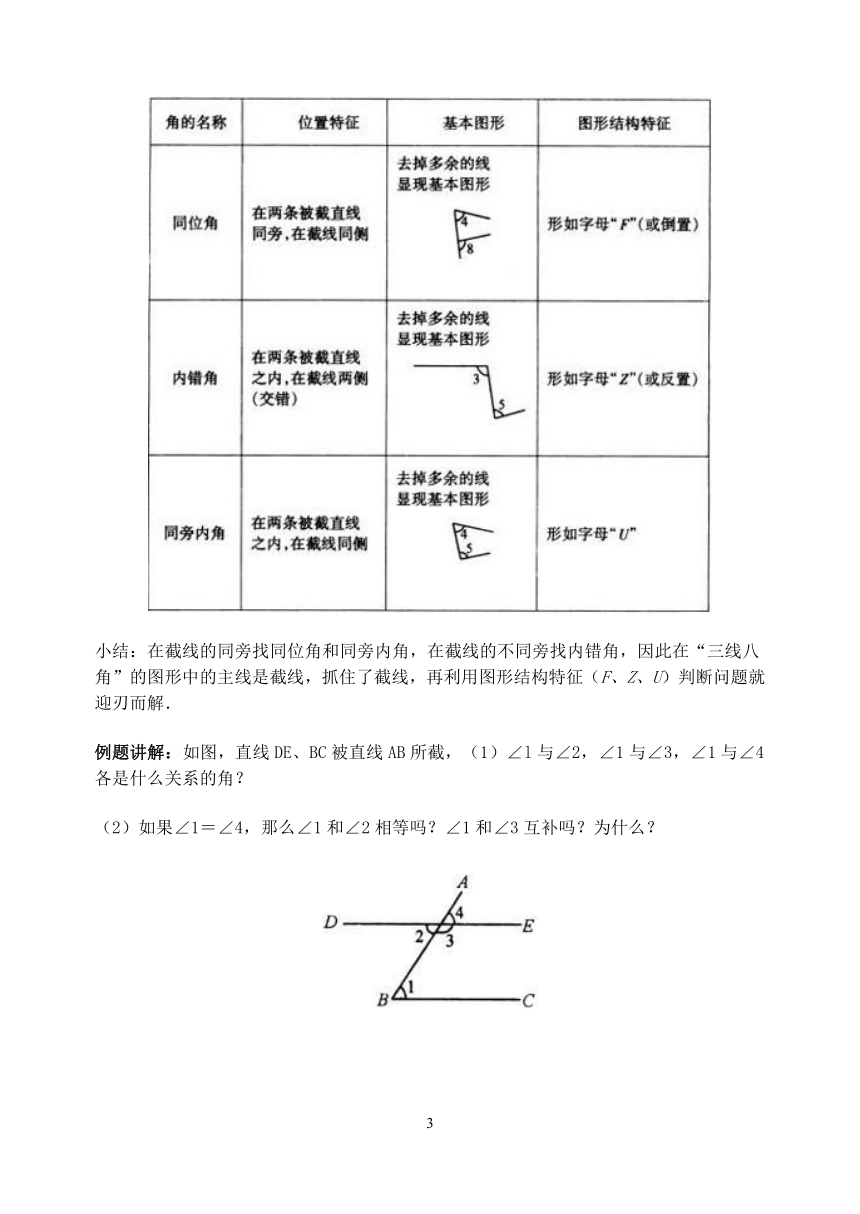
(1)同位角:分别在被截直线同方向,截线的同侧,即它们的位置相同,这样的两个角叫做同位角.
问题:∠1和∠5有什么共同特点?
均在直线l3的一侧,且分别在l1和l2的上方,像这样的两个角叫作同位角.
请同学们指出:图中还有同位角吗?(答:∠2与∠6,∠4与∠8,∠3与∠7)
(2)内错角:分别在被截直线内,截线的两侧,这样的两个角叫做内错角.
(3)同旁内角:分别在被截直线内,截线同侧(同旁),这样的两个角叫做同旁内角.
提问:(1)同位角和同旁内角在位置上有什么相同点和不同点?
(2)内错角和同旁内角在位置上有什么相同点和不同点?
(3)这三类角的共同特征是什么?
小结:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中的主线是截线,抓住了截线,再利用图形结构特征(F、Z、U)判断问题就迎刃而解.
例题讲解:如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
变式练习
1.如图2-32,说出以下各对角是哪两条直线被第三条直线所截而得到的?∠1与∠2,∠2与∠4,∠2与∠3.
答:∠1与∠2是l2、l3被l1所截而得到的一对同旁内角.
∠2与∠4是直线l2、l1被l3所截而得到的同旁内角.
∠2与∠3是l2、l1被l3所截而得到的同位角.
2.如图2-33,找出下列图中的同位角,内错角和同旁内角.
答:同位角有:∠2与∠3,∠4与∠7,∠4与∠8;内错角有∠1与∠3,∠6与∠8,∠6与∠7;同旁内角有∠3与∠8,∠1与∠4.
说明:一看角的顶点;二看角的边;三看角的方位.这“三看”又离不开主线——截线的确定
3.如图2-34,指出图中∠1与∠2,∠3与∠4的关系.
答:∠1与∠2是内错角,∠3与∠4也是内错角.
正确识别这三类角应注意的问题:
(1)识别这三类角首先要抓住“三条线”,即:哪两条直线被哪一条直线所截.
(2)抓住“截线”,截线的同侧有哪些角、从中找同位角和同旁内角,在截线的两侧找内错角.
课堂练习
1. 找出如图2-35中的对顶角和邻补角.
答:对顶角有四对,它们是∠1与∠3,∠2与∠4,∠5与∠6,∠7与∠8;
邻补角有∠1与∠2,∠2与∠3,∠3与∠4,∠4与∠1,∠5与∠8,∠8与∠6,∠6与∠7,∠7与∠5.
(还可以找出图2-35中相等的角,即四对对顶角)
2.如图2-36,如果∠1=∠2=∠7,那么还有哪些角是相等的.
答:∠1与∠4是邻补角.∠2与∠5是邻补角,∠3与∠6是邻补角.∠7与∠8是邻补角,因为∠1=∠2=∠7,∠2=∠3(对顶角相等),所以∠1=∠2=∠3=∠7,则∠4=∠5=∠6=∠8.(等角的补角相等)
3.如图2-37中,若∠1=∠2,证明:∠3与∠4是互补的角.
证明:因为∠1=∠3,(对顶角相等)
∠1=∠2,(已知)
所以∠2=∠3.(等量代换)
又因为∠2+∠4=180°,
所以∠3+∠4=180°.(等量代换)
即∠3与∠4是互补的角.
此题在证明的分析中,可以用以下逻辑思考的过程,即“执果索因”法.
若要证∠3与∠4互补,即证∠3+∠4=180°,但∠4与∠2的和为180°,因此需证∠3=∠2,由于∠3=∠1(对顶角相等),∠1=∠2是已知,所以∠2=∠3.而写出证明过程时,要从先证∠2=∠3出发,最后得到∠3+∠4=180°.
以上的几何证明题的思考过程是一种常见的方法,它是从要证明结果的出发,探索要得出这个结果时,应具备的条件,只要将条件准备充足,就能得到要求的结果.
小结
(1)学了哪些相互关系的角?
答:学过六种相互关系的角.
①互为余角,②互为补角(邻补角是特殊情形),③对顶角,④同位角,⑤内错角,⑥同旁内角.
(2)寻找同位的、内错角和同旁内角关键应准确找到什么?
答:寻找同位角,同旁内角关键在于准确找到三线中的主线——截线.(两线被第三线所截)
(3)相交直线:
板书设计
PAGE
4
【教学目标】
知识与技能
1.使学生理解三线八角的意义,并能从复杂图形中识别它们.
2.通过三线八角的特点的分析,培养学生抽象概括问题的能力.
3.使学生认识图形是由简到繁组合而成,培养学生形成基本图形结构的能力.
过程与方法
通过学生探索三条直线的位置关系引入三线八角的概念,在学生探索的过程中加深学生对概念的理解,通过具体的例题使学生掌握在复杂图形中识别三线八角的方法。
情感态度与价值观
培养学生的探索归纳能力
【教学重点】
三线八角的意义
【教学难点】
能在各种变式的图形中找出这三类角
【教学过程】
复习提问
前面我们学习了相交线,两条直线相交后产生了几个角?每两个角之间的关系是什么?
(除平角外,产生四个角,对顶角相等,邻补角互补)
引入新课
三条直线之间可以有什么样的位置关系?(请你用三支笔表示三条直线,来排放一下可能存在的位置关系。)
(1)三条直线都平行(没有交点).
(2)两条直线平行被第三条直线所截(两个交点).
(3)三条直线两两相交(有三个交点).
(4)三条直线交于一点(一个交点).
前面我们对相交的两条直线所形成的四个角进行研究,今天我们就对三条直线相交后形成的八个角如图2-30(3)进行研究,简称为:三线八角.(板书课题)
新课讲解
在图2-31中,l1和l3(或l2和l3)所形成的四个角是有公共顶点的,而每两个角之间的关系从位置来分,可分为两类:对顶角和邻补角,而上面四个角和下面四个角是没有公共顶点的,那么上面的一个与下面的一个又有什么样的位置关系呢?这就是下面所要研究的问题.
(1)同位角:分别在被截直线同方向,截线的同侧,即它们的位置相同,这样的两个角叫做同位角.
问题:∠1和∠5有什么共同特点?
均在直线l3的一侧,且分别在l1和l2的上方,像这样的两个角叫作同位角.
请同学们指出:图中还有同位角吗?(答:∠2与∠6,∠4与∠8,∠3与∠7)
(2)内错角:分别在被截直线内,截线的两侧,这样的两个角叫做内错角.
(3)同旁内角:分别在被截直线内,截线同侧(同旁),这样的两个角叫做同旁内角.
提问:(1)同位角和同旁内角在位置上有什么相同点和不同点?
(2)内错角和同旁内角在位置上有什么相同点和不同点?
(3)这三类角的共同特征是什么?
小结:在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中的主线是截线,抓住了截线,再利用图形结构特征(F、Z、U)判断问题就迎刃而解.
例题讲解:如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
变式练习
1.如图2-32,说出以下各对角是哪两条直线被第三条直线所截而得到的?∠1与∠2,∠2与∠4,∠2与∠3.
答:∠1与∠2是l2、l3被l1所截而得到的一对同旁内角.
∠2与∠4是直线l2、l1被l3所截而得到的同旁内角.
∠2与∠3是l2、l1被l3所截而得到的同位角.
2.如图2-33,找出下列图中的同位角,内错角和同旁内角.
答:同位角有:∠2与∠3,∠4与∠7,∠4与∠8;内错角有∠1与∠3,∠6与∠8,∠6与∠7;同旁内角有∠3与∠8,∠1与∠4.
说明:一看角的顶点;二看角的边;三看角的方位.这“三看”又离不开主线——截线的确定
3.如图2-34,指出图中∠1与∠2,∠3与∠4的关系.
答:∠1与∠2是内错角,∠3与∠4也是内错角.
正确识别这三类角应注意的问题:
(1)识别这三类角首先要抓住“三条线”,即:哪两条直线被哪一条直线所截.
(2)抓住“截线”,截线的同侧有哪些角、从中找同位角和同旁内角,在截线的两侧找内错角.
课堂练习
1. 找出如图2-35中的对顶角和邻补角.
答:对顶角有四对,它们是∠1与∠3,∠2与∠4,∠5与∠6,∠7与∠8;
邻补角有∠1与∠2,∠2与∠3,∠3与∠4,∠4与∠1,∠5与∠8,∠8与∠6,∠6与∠7,∠7与∠5.
(还可以找出图2-35中相等的角,即四对对顶角)
2.如图2-36,如果∠1=∠2=∠7,那么还有哪些角是相等的.
答:∠1与∠4是邻补角.∠2与∠5是邻补角,∠3与∠6是邻补角.∠7与∠8是邻补角,因为∠1=∠2=∠7,∠2=∠3(对顶角相等),所以∠1=∠2=∠3=∠7,则∠4=∠5=∠6=∠8.(等角的补角相等)
3.如图2-37中,若∠1=∠2,证明:∠3与∠4是互补的角.
证明:因为∠1=∠3,(对顶角相等)
∠1=∠2,(已知)
所以∠2=∠3.(等量代换)
又因为∠2+∠4=180°,
所以∠3+∠4=180°.(等量代换)
即∠3与∠4是互补的角.
此题在证明的分析中,可以用以下逻辑思考的过程,即“执果索因”法.
若要证∠3与∠4互补,即证∠3+∠4=180°,但∠4与∠2的和为180°,因此需证∠3=∠2,由于∠3=∠1(对顶角相等),∠1=∠2是已知,所以∠2=∠3.而写出证明过程时,要从先证∠2=∠3出发,最后得到∠3+∠4=180°.
以上的几何证明题的思考过程是一种常见的方法,它是从要证明结果的出发,探索要得出这个结果时,应具备的条件,只要将条件准备充足,就能得到要求的结果.
小结
(1)学了哪些相互关系的角?
答:学过六种相互关系的角.
①互为余角,②互为补角(邻补角是特殊情形),③对顶角,④同位角,⑤内错角,⑥同旁内角.
(2)寻找同位的、内错角和同旁内角关键应准确找到什么?
答:寻找同位角,同旁内角关键在于准确找到三线中的主线——截线.(两线被第三线所截)
(3)相交直线:
板书设计
PAGE
4
