列方程解应用题[下学期]
图片预览





文档简介
课件12张PPT。一、复习1、列一元一次方程解应用题的步骤有哪些? 应认真审题,分析题中的数量关系,用字母表示题目中的未知数时一般采用直接设法,当直接设法使列方程有困难可采用间接设法,注意未知数的单位不要漏写。 可借助图表分析题中的已知量和未知量之间关系,列出等式两边的代数式,注意它们的量要一致,使它们都表示一个相等或相同的量。 列方程应满足三个条件:各类是同类量,单位一致,两边是等量。(1)设未知数(2)寻找相等关系(3)列方程 方程的变形应根据等式性质和运算法则。 检查方程的解是否符合应用题的实际意义,进行取舍,并注意单位。2、解行程问题的应用题要用到路程、速度、时间之间的关系,如果用s、v、t分别表示路程、速度、时间,那么s、v、t三个量的关系为s= ,或v= ,或t= 。3、相向而行同时出发到相遇时甲、乙两人所用的时间
,同向而行同时出发到相遇(即追击)时,甲、乙两人所用的时间 。4、甲、乙相向而行的相遇问题中相等关系是:_________ , 甲、乙同向而行的追击问题中(甲追乙)相等关系是
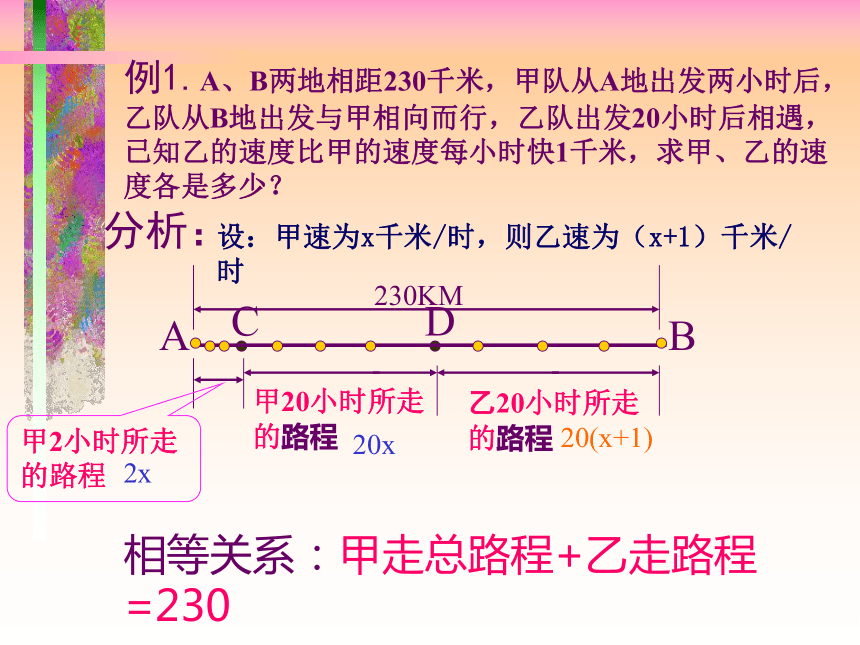
______________________________________。S/tvtS/v相等相等甲的行程+乙的行程=甲、乙的起始路程甲的行程-乙的行程=甲、乙的起始路程(4)解方程(5)写出答案例1.A、B两地相距230千米,甲队从A地出发两小时后,乙队从B地出发与甲相向而行,乙队出发20小时后相遇,已知乙的速度比甲的速度每小时快1千米,求甲、乙的速度各是多少?分析:CD相等关系:甲走总路程+乙走路程=2302x20x20(x+1)设:甲速为x千米/时,则乙速为(x+1)千米/时解:设甲的速度为x千米/时,则乙的速度为(x+1)千米/时,根据题意,得
答:甲、乙的速度各是5千米/时、6千米/时2x+20x+20(x+1)=2302x+20x+20x+20=23042x=210x=5∴乙的速度为 x+1=5+1=61、甲、乙骑自行车同时从相距 65千米的两地相向而行,2小时相遇。甲比乙每小时多骑2.5千米,求乙的时速。解:设乙的速度为x千米/时,则甲的速度为(x+2.5)千米/时,根据题意,得
2(x+2.5)+2x=65
2x+5+2x=65
4x=60
X=15
答:乙的时速为15千米/时。课练一2、甲、乙两站间的路程为365KM。一列慢车从甲站开往乙站,每小时行驶65KM;慢车行驶了1小时后,另有一列快车从乙站开往甲站,每小时行驶85KM。快车行驶了几小时与慢车相遇?(只列方程不解)解:快车行驶了x小时后与慢车相遇,根据题意,得
65+x(65+85)=365例2、甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?分析:CB设x小时后乙车追上甲车相等关系:
甲走的路程=乙走的路程 48x 72x 解:设乙车开出x小时后追上甲车,根据题意,得24x=20甲、乙两位同学练习赛跑,甲每秒跑7米,乙每秒跑6.5米。(1)如果甲让乙先跑5米,几秒钟后甲可以追上乙? (2)如果甲让乙先跑1秒,几秒钟后甲可以追上乙?解:(1)设x秒后甲可以追上乙,根据题意,得(2)设x秒后甲可以追上乙,根据题意,得课练二、(只列方程不解)7x-6.5x=57x-6.5x=6.5练习册 P88—89 第7题---第12题 速度时间三、小结1、行程问题中的相等关系是:路程=_____×_____。2、相遇问题常用的等量关系是:3、追击问题常用的等量关系是:四、作业 行程和=速度和×相遇时间。行程差=速度差×追击时间。同学们,再见!
,同向而行同时出发到相遇(即追击)时,甲、乙两人所用的时间 。4、甲、乙相向而行的相遇问题中相等关系是:_________ , 甲、乙同向而行的追击问题中(甲追乙)相等关系是
______________________________________。S/tvtS/v相等相等甲的行程+乙的行程=甲、乙的起始路程甲的行程-乙的行程=甲、乙的起始路程(4)解方程(5)写出答案例1.A、B两地相距230千米,甲队从A地出发两小时后,乙队从B地出发与甲相向而行,乙队出发20小时后相遇,已知乙的速度比甲的速度每小时快1千米,求甲、乙的速度各是多少?分析:CD相等关系:甲走总路程+乙走路程=2302x20x20(x+1)设:甲速为x千米/时,则乙速为(x+1)千米/时解:设甲的速度为x千米/时,则乙的速度为(x+1)千米/时,根据题意,得
答:甲、乙的速度各是5千米/时、6千米/时2x+20x+20(x+1)=2302x+20x+20x+20=23042x=210x=5∴乙的速度为 x+1=5+1=61、甲、乙骑自行车同时从相距 65千米的两地相向而行,2小时相遇。甲比乙每小时多骑2.5千米,求乙的时速。解:设乙的速度为x千米/时,则甲的速度为(x+2.5)千米/时,根据题意,得
2(x+2.5)+2x=65
2x+5+2x=65
4x=60
X=15
答:乙的时速为15千米/时。课练一2、甲、乙两站间的路程为365KM。一列慢车从甲站开往乙站,每小时行驶65KM;慢车行驶了1小时后,另有一列快车从乙站开往甲站,每小时行驶85KM。快车行驶了几小时与慢车相遇?(只列方程不解)解:快车行驶了x小时后与慢车相遇,根据题意,得
65+x(65+85)=365例2、甲、乙两车自西向东行驶,甲车的速度是每小时48千米,乙车的速度是每小时72千米,甲车开出25分钟后乙车开出,问几小时后乙车追上甲车?分析:CB设x小时后乙车追上甲车相等关系:
甲走的路程=乙走的路程 48x 72x 解:设乙车开出x小时后追上甲车,根据题意,得24x=20甲、乙两位同学练习赛跑,甲每秒跑7米,乙每秒跑6.5米。(1)如果甲让乙先跑5米,几秒钟后甲可以追上乙? (2)如果甲让乙先跑1秒,几秒钟后甲可以追上乙?解:(1)设x秒后甲可以追上乙,根据题意,得(2)设x秒后甲可以追上乙,根据题意,得课练二、(只列方程不解)7x-6.5x=57x-6.5x=6.5练习册 P88—89 第7题---第12题 速度时间三、小结1、行程问题中的相等关系是:路程=_____×_____。2、相遇问题常用的等量关系是:3、追击问题常用的等量关系是:四、作业 行程和=速度和×相遇时间。行程差=速度差×追击时间。同学们,再见!
