2023年九年级数学中考复习:二次函数的应用(含答案)
文档属性
| 名称 | 2023年九年级数学中考复习:二次函数的应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 581.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 21:16:45 | ||
图片预览



文档简介
2023年春九年级数学中考复习《二次函数的应用》考前冲刺训练(附答案)
(共12小题,每小题10分,满分120分)
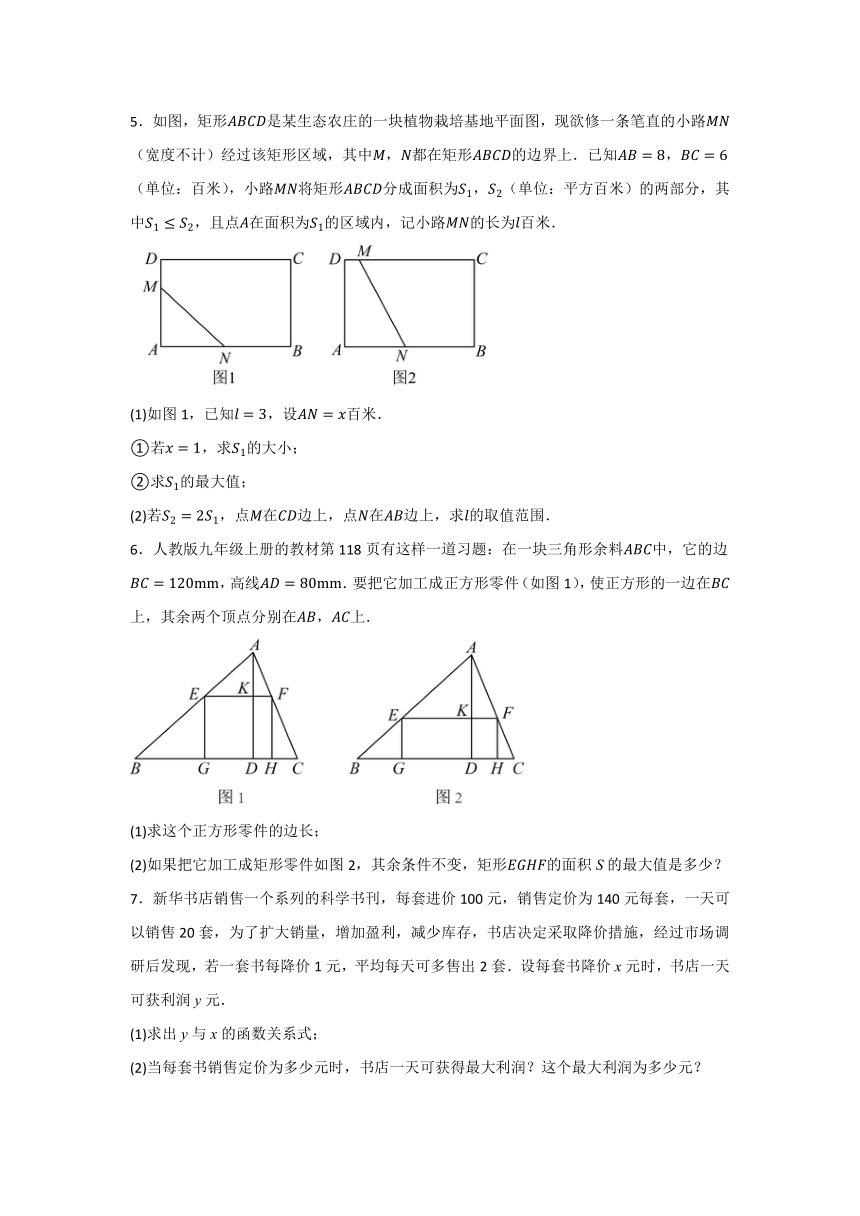
1.图1是一个倾斜角为α的斜坡的横截面.斜坡顶端B与地面的距离为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,与喷头A的水平距离为6米(单位:米)(水珠的竖直高度是指水珠与水平地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足二次函数关系,其中当水珠与喷头A的水平距离为4米时,喷出的水珠达到最大高度4米.
(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.9米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
2.如图,一个横截面为抛物线形的公路隧道,其最大高度6米,底部宽度为12米,现以O点为原点,所在的直线为x轴建立直角坐标系.
(1)求这条抛物线的表达式;
(2)该隧道设计为双向通行道,如果规定车辆必须在中心线两侧、距离道路边缘2米的范围内行使,并保持车辆顶部与隧道有不少于米的空隙,则通过隧道车辆的高度限制应为_ 米;
(3)在隧道修建过程中,需要搭建矩形支架(由三段组成)对隧道进行装饰,其中C、D在抛物线上,A,B在地面上,求这个支架总长Z的最大值.
3.数学活动小组通过观察投掷铅球的运行轨迹来研究二次函数的性质:在投掷铅球的实验中,该铅球运行的高度与水平距离之间的关系式是二次函数.小明投掷铅球出手时离地面的高度为,经测量铅球落地成绩刚好是(铅球成绩达到是满分).
(1)写出的取值范围是_______;
(2)若小明投掷的铅球运行到水平距离为时,铅球达到最大高度,求该铅球运行路线的解析式;
(3)已知小红投掷铅球出手时离地面的高度为,,
①若小红投掷铅球成绩也是满分,求的取值范围;
②若小红投掷铅球成绩刚好是,求:小红投掷铅球的运行水平距离为多少米时与(2)中小明投掷铅球的运行路线的高度差最大?
4.如图(1)所示,濮阳湿地公园中,金堤河大桥是一座非常有艺术性造型的大桥.桥身是由两条抛物线钢架建造.如图(2)所示,两条抛物线有共同的对称轴,已知,过原点,两抛物线最高点的距离为.
(1)求抛物线的解析式;
(2)①求主桥长为多少米?
②过点与轴平行的直线为河面的水平线,,若要在与水面的交点、处建造两个桥墩,其中一个桥墩到岸边(轴)的距离是多少米?(说明:题中个单位长为米)
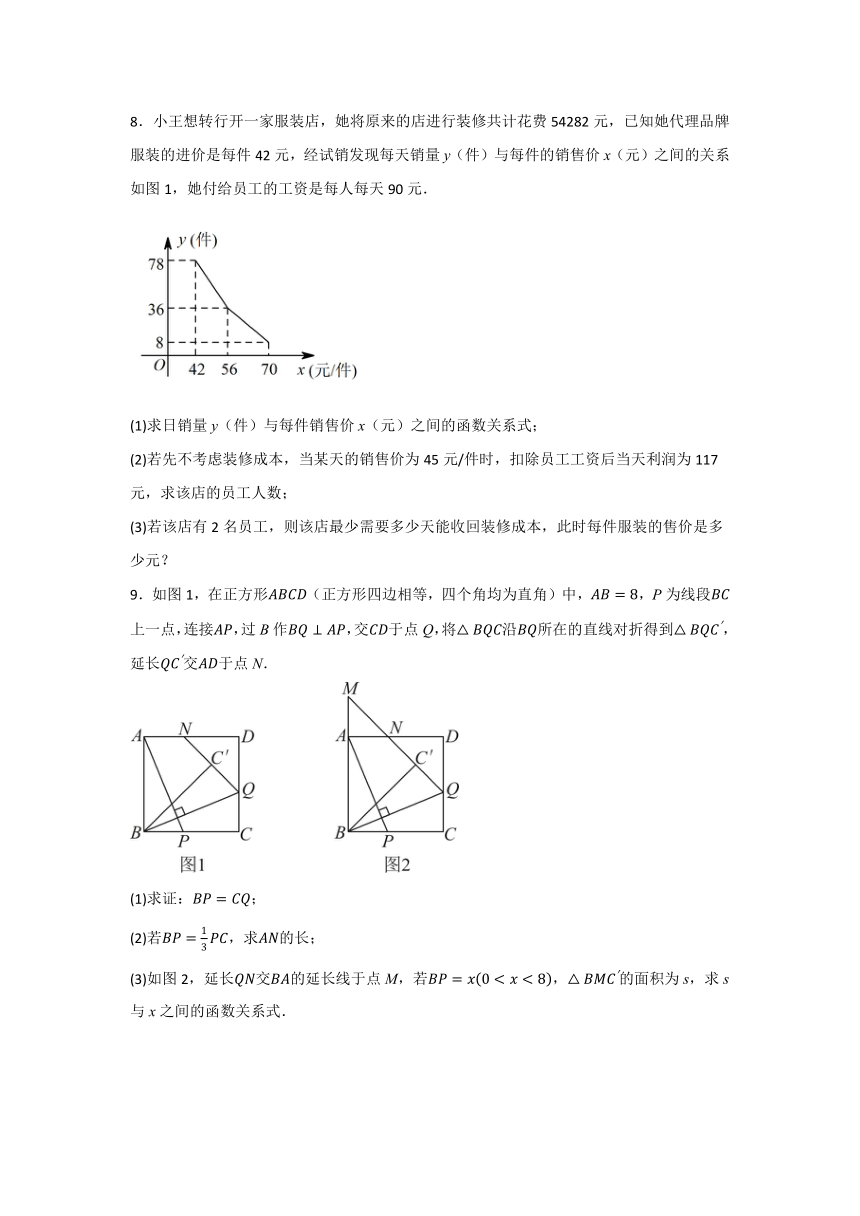
5.如图,矩形是某生态农庄的一块植物栽培基地平面图,现欲修一条笔直的小路(宽度不计)经过该矩形区域,其中,都在矩形的边界上.已知,(单位:百米),小路将矩形分成面积为,(单位:平方百米)的两部分,其中,且点在面积为的区域内,记小路的长为百米.
(1)如图1,已知,设百米.
①若,求的大小;
②求的最大值;
(2)若,点在边上,点在边上,求的取值范围.
6.人教版九年级上册的教材第118页有这样一道习题:在一块三角形余料中,它的边,高线.要把它加工成正方形零件(如图1),使正方形的一边在上,其余两个顶点分别在,上.
(1)求这个正方形零件的边长;
(2)如果把它加工成矩形零件如图2,其余条件不变,矩形的面积S的最大值是多少?
7.新华书店销售一个系列的科学书刊,每套进价100元,销售定价为140元每套,一天可以销售20套,为了扩大销量,增加盈利,减少库存,书店决定采取降价措施,经过市场调研后发现,若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.
(1)求出y与x的函数关系式;
(2)当每套书销售定价为多少元时,书店一天可获得最大利润?这个最大利润为多少元?
8.小王想转行开一家服装店,她将原来的店进行装修共计花费54282元,已知她代理品牌服装的进价是每件42元,经试销发现每天销量y(件)与每件的销售价x(元)之间的关系如图1,她付给员工的工资是每人每天90元.
(1)求日销量y(件)与每件销售价x(元)之间的函数关系式;
(2)若先不考虑装修成本,当某天的销售价为45元/件时,扣除员工工资后当天利润为117元,求该店的员工人数;
(3)若该店有2名员工,则该店最少需要多少天能收回装修成本,此时每件服装的售价是多少元?
9.如图1,在正方形(正方形四边相等,四个角均为直角)中,,P为线段上一点,连接,过B作,交于点Q,将沿所在的直线对折得到,延长交于点N.
(1)求证:;
(2)若,求的长;
(3)如图2,延长交的延长线于点M,若,的面积为s,求s与x之间的函数关系式.
10.某商场准备购进A、B两种商品进行销售,已知一件A种商品的进价比一件B种商品的进价多10元,且用16000元采购A种商品件数是用7500元采购B种商品件数的2倍.
(1)每件A种和B种商品的进价分别为多少元?
(2)该商场欲购进A,B两种商品共250件进行销售,其中A种商品件数不小于20件,且不大于B种商品件数.
若B种商品的售价定为210元/件,A种商品的售价与A种商品销量之间的关系如下表所示:
A种商品的销量 0 5 10 15 20 ……
A种商品的售价 240 230 220 210 200 ……
商场购进这两种商品能全部售出的前提下,请求出该商场销售这两种商品能获得的最大利润,并求出此时的进货方案.
11.某市公安局交警支队在全市范围内开展“一盔一带”安全守护行动,某商场的头盔销量不断增加,该头盔销售第天与该天销售量(件)之间满足函数关系式为:(且为整数),为减少库存,该商场将此头盔的价格不断下调,其销售单价(元)与第天成一次函数关系,当时,,当时,.已知该头盔进价为元/件.
(1)求与之同的函数关系式;
(2)求这天中第几天销售利润最大,并求出最大利润;
(3)在实际销售的前天,为配合“骑乘人员佩戴头盔专题周”活动的开展,商场决定将每个头盔的单价在原来价格变化的基上再降价元()销售,通过销售记录发现,前8天中,每天的利润随时间(天)的增大而增大,试求的取值范围.
12.综合与探究
如图,抛物线与x轴交于,两点,与y轴交于点C.现有一宽度为1,长度足够长的矩形(图中阴影部分),矩形的长与y轴平行,将矩形沿x轴方向平移,矩形交抛物线于点M,N(点M在点N的左侧),交直线于点E,F(点E在点F的左侧),设点M的横坐标为m().
(1)求抛物线的函数表达式;
(2)在矩形平移的过程中,如果以点E,F,N,M为顶点的四边形是平行四边形,求出此时m的值;
(3)点P是直线上一动点,点Q为抛物线顶点,若,请直接写出点P的坐标.
参考答案
1.解:(1)根据题意可得:抛物线顶点坐标,且过,过,
设抛物线解析式为,
解得
关于的函数关系式为.
(2)设树的竖直高度为h,则,
得:,
当时,,
所以水珠能越过这棵树.
2.(1)解:由题意知:抛物线的顶点,
设抛物线的表达式为
将代入,得:,
抛物线表达式为:;
(2)解:把或代入中,得,
车辆顶部与隧道有不少于米的空隙,
限高为米,
故答案为:3;
(3)解:设,
矩形支架,
轴,,
与C关于直线对称,
,
,
当时,Z有最大值15,
3.(1)解:∵成绩刚好是,
∴,
∴,
故答案为:.
(2)根据题意,经过点,
∴,
解得,
∴抛物线的解析式为.
(3)①解:根据离地面的高度为,,得到,
∴,
∴,
∴,
解得,
故b的取值范围为:.
②设高度差为,
,
∵,
∴有最大值,且当时,取得最大值,
故铅球的运行水平距离为时与(2)中小明投掷铅球的运行路线的高度差最大.
4.(1)解:由题知:
则抛物线对称轴为,最高点
∵过原点,两抛物线最高点的距离为.
∴设抛物线的解析式为
把点代入得
∴抛物线的解析式为
(2)①令,则
解得,,
∴
答:主桥长为米
②由题知:令,则
解得:或(舍去),
,
答:其中一个桥墩E到岸边(轴)的距离是米
5.(1)解:①∵四边形是矩形,,,
∴,
∴在中,,
∵,,
∴,
∴,
∴的大小为;
②∵(当时取等号),
∴,
当时,,
∴的最大值为.
(2)如图,过点作于点,
∵四边形是矩形,
∴,
∵四边形是矩形,
∴,,
在矩形中,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴
,
∴当时,取最小值,
当或时,取最大值,
∴的取值范围是.
6.解:(1)∵四边形为正方形,
∴,,,
∴.
∵,
∴,
即结合,可得是矩形,
∴,
设正方形零件的边长为,则,
即.
∵,,,
∴,
∴,
解得.
答:这个正方形零件的边长是;
(2)设,根据(1)可得,
∵矩形,
∴,
∴,
∴,
∴,
∴,
∴矩形面积,
当时,此时矩形面积最大,最大面积是,
即:矩形面积最大是.
7.解:(1)由题意可知:
化简为:
∴y与x的函数关系式为:
(2)由题意得
∵
∴当时,y最大为1250.此时售价为元.
答:当售价定为125元时,获利最大,利润最大为1250元.
8.解:(1)当时,设,
∴,解得,
∴,
当时,设,
∴,解得,
∴,
∴综上所述,;
(2)设该店的员工人数为m,
∴,
∴解得,
∴该店的员工人数为1.
(3)当时,
每天的利润,
∵,
∴当时,每天的利润最大为327元;
当时,
每天的利润,
∴当时,每天的利润最大为332元;
∵,
∴当时,每天的利润最大,
∴(天),
∴该店有2名员工,则该店最少需要164天能收回装修成本,此时每件服装的售价是58元.
9.解:(1)证明:∵,
∴,
∵,
∴,
∴,
在于△BCQ中,
,
∴,
∴;
(2)解:由翻折可知,,
连接,在和中,,
∴,
∴,
∵,,,
∴,,
设,则,
根据勾股定理得,,
∴,
即.
(3)解:过Q点作于G,由(1)知,.
设,则,
∴在中,,
∴,
∴,
∴.
10.(1)解:设每件A种商品的进价x元,则每件B种商品的进价为元,
根据题意,得,
解得:,
经检验:是方程的根,
,
答:每件A种商品的进价160元,每件B种商品的进价为150元.
(2)解:设销售A种商品销量m件,则销售B种商品件,
根据题意可得:,
解得,
由表格中的数据可知:A种商品的售价y与A种商品销量m满足一次函数关系,设为,
由题意可得;,解得,
∴,
设获得的利润w元,
则
,
∵,
∴当时,w随m的增大而减小,
∵,
∴当时,w有最大值为元;
此时进货方案为:A种商品进20件,B种商品进230件;
答:该商场销售这两种商品能获得的最大利润为14600元,此时的进货方案是A种商品进20件,B种商品进230件.
11.(1)解:根据题意,设,当时,,当时,,
∴,解得:,
∴与之间的函数关系式为().
(2)解:设总利润为元,则
,
当时,取得最大值,
∴第天利润最大,最大值为:(元).
(3)解:由题意可设第天的销售利润为元,则
,
∴对称轴为
又知前天中,每天的利润随时间(天)的增大而增大,
∴即,
又,
∴.
12.(1)解:将,代入.
得:,解得:,
∴;
(2)当时,,∴.
设直线的表达式为,
将代入得:,
∴,∴.
∵,则,
∴,
∵矩形的宽为1,
∴点N的纵坐标为:,则F的纵坐标为:.
∵以点E,F,N,M为顶点的四边形是平行四边形,
∴,即.
解得:或,
∵,
∴m的值为1或.
(3)(3)存在,点P的坐标为,.
①当点P在直线的右侧时,
∵,
∴顶点Q的坐标为,
连接,
可得直线的解析式为,
∴直线与y轴的交点为,
∴,,,
∵,
∴设A,C,Q三点共圆,则,
∵,
∴,
∴,
∴,
∴,
∴,
∴直线的解析式为,
解方程组,得,
∴;
②当点P在直线的左侧时,此时点与点关于直线对称,
过点作直线的垂线,交于点F,取,
∵直线的解析式为,
∴设直线的解析式为,代入点,
得,解得,
∴直线的解析式为,
解方程组,得,
∴,
∵点向左平移个单位,再向下平移个单位得到点F,
∴点F向左平移个单位,再向下平移个单位得到点E,
∴,
∴直线的解析式为,
解方程组,得,
∴,
∴存在,点P的坐标为,.
(共12小题,每小题10分,满分120分)
1.图1是一个倾斜角为α的斜坡的横截面.斜坡顶端B与地面的距离为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,与喷头A的水平距离为6米(单位:米)(水珠的竖直高度是指水珠与水平地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足二次函数关系,其中当水珠与喷头A的水平距离为4米时,喷出的水珠达到最大高度4米.
(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.9米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
2.如图,一个横截面为抛物线形的公路隧道,其最大高度6米,底部宽度为12米,现以O点为原点,所在的直线为x轴建立直角坐标系.
(1)求这条抛物线的表达式;
(2)该隧道设计为双向通行道,如果规定车辆必须在中心线两侧、距离道路边缘2米的范围内行使,并保持车辆顶部与隧道有不少于米的空隙,则通过隧道车辆的高度限制应为_ 米;
(3)在隧道修建过程中,需要搭建矩形支架(由三段组成)对隧道进行装饰,其中C、D在抛物线上,A,B在地面上,求这个支架总长Z的最大值.
3.数学活动小组通过观察投掷铅球的运行轨迹来研究二次函数的性质:在投掷铅球的实验中,该铅球运行的高度与水平距离之间的关系式是二次函数.小明投掷铅球出手时离地面的高度为,经测量铅球落地成绩刚好是(铅球成绩达到是满分).
(1)写出的取值范围是_______;
(2)若小明投掷的铅球运行到水平距离为时,铅球达到最大高度,求该铅球运行路线的解析式;
(3)已知小红投掷铅球出手时离地面的高度为,,
①若小红投掷铅球成绩也是满分,求的取值范围;
②若小红投掷铅球成绩刚好是,求:小红投掷铅球的运行水平距离为多少米时与(2)中小明投掷铅球的运行路线的高度差最大?
4.如图(1)所示,濮阳湿地公园中,金堤河大桥是一座非常有艺术性造型的大桥.桥身是由两条抛物线钢架建造.如图(2)所示,两条抛物线有共同的对称轴,已知,过原点,两抛物线最高点的距离为.
(1)求抛物线的解析式;
(2)①求主桥长为多少米?
②过点与轴平行的直线为河面的水平线,,若要在与水面的交点、处建造两个桥墩,其中一个桥墩到岸边(轴)的距离是多少米?(说明:题中个单位长为米)
5.如图,矩形是某生态农庄的一块植物栽培基地平面图,现欲修一条笔直的小路(宽度不计)经过该矩形区域,其中,都在矩形的边界上.已知,(单位:百米),小路将矩形分成面积为,(单位:平方百米)的两部分,其中,且点在面积为的区域内,记小路的长为百米.
(1)如图1,已知,设百米.
①若,求的大小;
②求的最大值;
(2)若,点在边上,点在边上,求的取值范围.
6.人教版九年级上册的教材第118页有这样一道习题:在一块三角形余料中,它的边,高线.要把它加工成正方形零件(如图1),使正方形的一边在上,其余两个顶点分别在,上.
(1)求这个正方形零件的边长;
(2)如果把它加工成矩形零件如图2,其余条件不变,矩形的面积S的最大值是多少?
7.新华书店销售一个系列的科学书刊,每套进价100元,销售定价为140元每套,一天可以销售20套,为了扩大销量,增加盈利,减少库存,书店决定采取降价措施,经过市场调研后发现,若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.
(1)求出y与x的函数关系式;
(2)当每套书销售定价为多少元时,书店一天可获得最大利润?这个最大利润为多少元?
8.小王想转行开一家服装店,她将原来的店进行装修共计花费54282元,已知她代理品牌服装的进价是每件42元,经试销发现每天销量y(件)与每件的销售价x(元)之间的关系如图1,她付给员工的工资是每人每天90元.
(1)求日销量y(件)与每件销售价x(元)之间的函数关系式;
(2)若先不考虑装修成本,当某天的销售价为45元/件时,扣除员工工资后当天利润为117元,求该店的员工人数;
(3)若该店有2名员工,则该店最少需要多少天能收回装修成本,此时每件服装的售价是多少元?
9.如图1,在正方形(正方形四边相等,四个角均为直角)中,,P为线段上一点,连接,过B作,交于点Q,将沿所在的直线对折得到,延长交于点N.
(1)求证:;
(2)若,求的长;
(3)如图2,延长交的延长线于点M,若,的面积为s,求s与x之间的函数关系式.
10.某商场准备购进A、B两种商品进行销售,已知一件A种商品的进价比一件B种商品的进价多10元,且用16000元采购A种商品件数是用7500元采购B种商品件数的2倍.
(1)每件A种和B种商品的进价分别为多少元?
(2)该商场欲购进A,B两种商品共250件进行销售,其中A种商品件数不小于20件,且不大于B种商品件数.
若B种商品的售价定为210元/件,A种商品的售价与A种商品销量之间的关系如下表所示:
A种商品的销量 0 5 10 15 20 ……
A种商品的售价 240 230 220 210 200 ……
商场购进这两种商品能全部售出的前提下,请求出该商场销售这两种商品能获得的最大利润,并求出此时的进货方案.
11.某市公安局交警支队在全市范围内开展“一盔一带”安全守护行动,某商场的头盔销量不断增加,该头盔销售第天与该天销售量(件)之间满足函数关系式为:(且为整数),为减少库存,该商场将此头盔的价格不断下调,其销售单价(元)与第天成一次函数关系,当时,,当时,.已知该头盔进价为元/件.
(1)求与之同的函数关系式;
(2)求这天中第几天销售利润最大,并求出最大利润;
(3)在实际销售的前天,为配合“骑乘人员佩戴头盔专题周”活动的开展,商场决定将每个头盔的单价在原来价格变化的基上再降价元()销售,通过销售记录发现,前8天中,每天的利润随时间(天)的增大而增大,试求的取值范围.
12.综合与探究
如图,抛物线与x轴交于,两点,与y轴交于点C.现有一宽度为1,长度足够长的矩形(图中阴影部分),矩形的长与y轴平行,将矩形沿x轴方向平移,矩形交抛物线于点M,N(点M在点N的左侧),交直线于点E,F(点E在点F的左侧),设点M的横坐标为m().
(1)求抛物线的函数表达式;
(2)在矩形平移的过程中,如果以点E,F,N,M为顶点的四边形是平行四边形,求出此时m的值;
(3)点P是直线上一动点,点Q为抛物线顶点,若,请直接写出点P的坐标.
参考答案
1.解:(1)根据题意可得:抛物线顶点坐标,且过,过,
设抛物线解析式为,
解得
关于的函数关系式为.
(2)设树的竖直高度为h,则,
得:,
当时,,
所以水珠能越过这棵树.
2.(1)解:由题意知:抛物线的顶点,
设抛物线的表达式为
将代入,得:,
抛物线表达式为:;
(2)解:把或代入中,得,
车辆顶部与隧道有不少于米的空隙,
限高为米,
故答案为:3;
(3)解:设,
矩形支架,
轴,,
与C关于直线对称,
,
,
当时,Z有最大值15,
3.(1)解:∵成绩刚好是,
∴,
∴,
故答案为:.
(2)根据题意,经过点,
∴,
解得,
∴抛物线的解析式为.
(3)①解:根据离地面的高度为,,得到,
∴,
∴,
∴,
解得,
故b的取值范围为:.
②设高度差为,
,
∵,
∴有最大值,且当时,取得最大值,
故铅球的运行水平距离为时与(2)中小明投掷铅球的运行路线的高度差最大.
4.(1)解:由题知:
则抛物线对称轴为,最高点
∵过原点,两抛物线最高点的距离为.
∴设抛物线的解析式为
把点代入得
∴抛物线的解析式为
(2)①令,则
解得,,
∴
答:主桥长为米
②由题知:令,则
解得:或(舍去),
,
答:其中一个桥墩E到岸边(轴)的距离是米
5.(1)解:①∵四边形是矩形,,,
∴,
∴在中,,
∵,,
∴,
∴,
∴的大小为;
②∵(当时取等号),
∴,
当时,,
∴的最大值为.
(2)如图,过点作于点,
∵四边形是矩形,
∴,
∵四边形是矩形,
∴,,
在矩形中,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴
,
∴当时,取最小值,
当或时,取最大值,
∴的取值范围是.
6.解:(1)∵四边形为正方形,
∴,,,
∴.
∵,
∴,
即结合,可得是矩形,
∴,
设正方形零件的边长为,则,
即.
∵,,,
∴,
∴,
解得.
答:这个正方形零件的边长是;
(2)设,根据(1)可得,
∵矩形,
∴,
∴,
∴,
∴,
∴,
∴矩形面积,
当时,此时矩形面积最大,最大面积是,
即:矩形面积最大是.
7.解:(1)由题意可知:
化简为:
∴y与x的函数关系式为:
(2)由题意得
∵
∴当时,y最大为1250.此时售价为元.
答:当售价定为125元时,获利最大,利润最大为1250元.
8.解:(1)当时,设,
∴,解得,
∴,
当时,设,
∴,解得,
∴,
∴综上所述,;
(2)设该店的员工人数为m,
∴,
∴解得,
∴该店的员工人数为1.
(3)当时,
每天的利润,
∵,
∴当时,每天的利润最大为327元;
当时,
每天的利润,
∴当时,每天的利润最大为332元;
∵,
∴当时,每天的利润最大,
∴(天),
∴该店有2名员工,则该店最少需要164天能收回装修成本,此时每件服装的售价是58元.
9.解:(1)证明:∵,
∴,
∵,
∴,
∴,
在于△BCQ中,
,
∴,
∴;
(2)解:由翻折可知,,
连接,在和中,,
∴,
∴,
∵,,,
∴,,
设,则,
根据勾股定理得,,
∴,
即.
(3)解:过Q点作于G,由(1)知,.
设,则,
∴在中,,
∴,
∴,
∴.
10.(1)解:设每件A种商品的进价x元,则每件B种商品的进价为元,
根据题意,得,
解得:,
经检验:是方程的根,
,
答:每件A种商品的进价160元,每件B种商品的进价为150元.
(2)解:设销售A种商品销量m件,则销售B种商品件,
根据题意可得:,
解得,
由表格中的数据可知:A种商品的售价y与A种商品销量m满足一次函数关系,设为,
由题意可得;,解得,
∴,
设获得的利润w元,
则
,
∵,
∴当时,w随m的增大而减小,
∵,
∴当时,w有最大值为元;
此时进货方案为:A种商品进20件,B种商品进230件;
答:该商场销售这两种商品能获得的最大利润为14600元,此时的进货方案是A种商品进20件,B种商品进230件.
11.(1)解:根据题意,设,当时,,当时,,
∴,解得:,
∴与之间的函数关系式为().
(2)解:设总利润为元,则
,
当时,取得最大值,
∴第天利润最大,最大值为:(元).
(3)解:由题意可设第天的销售利润为元,则
,
∴对称轴为
又知前天中,每天的利润随时间(天)的增大而增大,
∴即,
又,
∴.
12.(1)解:将,代入.
得:,解得:,
∴;
(2)当时,,∴.
设直线的表达式为,
将代入得:,
∴,∴.
∵,则,
∴,
∵矩形的宽为1,
∴点N的纵坐标为:,则F的纵坐标为:.
∵以点E,F,N,M为顶点的四边形是平行四边形,
∴,即.
解得:或,
∵,
∴m的值为1或.
(3)(3)存在,点P的坐标为,.
①当点P在直线的右侧时,
∵,
∴顶点Q的坐标为,
连接,
可得直线的解析式为,
∴直线与y轴的交点为,
∴,,,
∵,
∴设A,C,Q三点共圆,则,
∵,
∴,
∴,
∴,
∴,
∴,
∴直线的解析式为,
解方程组,得,
∴;
②当点P在直线的左侧时,此时点与点关于直线对称,
过点作直线的垂线,交于点F,取,
∵直线的解析式为,
∴设直线的解析式为,代入点,
得,解得,
∴直线的解析式为,
解方程组,得,
∴,
∵点向左平移个单位,再向下平移个单位得到点F,
∴点F向左平移个单位,再向下平移个单位得到点E,
∴,
∴直线的解析式为,
解方程组,得,
∴,
∴存在,点P的坐标为,.
同课章节目录
