20.1 平行四边形的判定[下学期]
文档属性
| 名称 | 20.1 平行四边形的判定[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 408.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-18 00:00:00 | ||
图片预览



文档简介
课件18张PPT。
用推理方法研究四边形
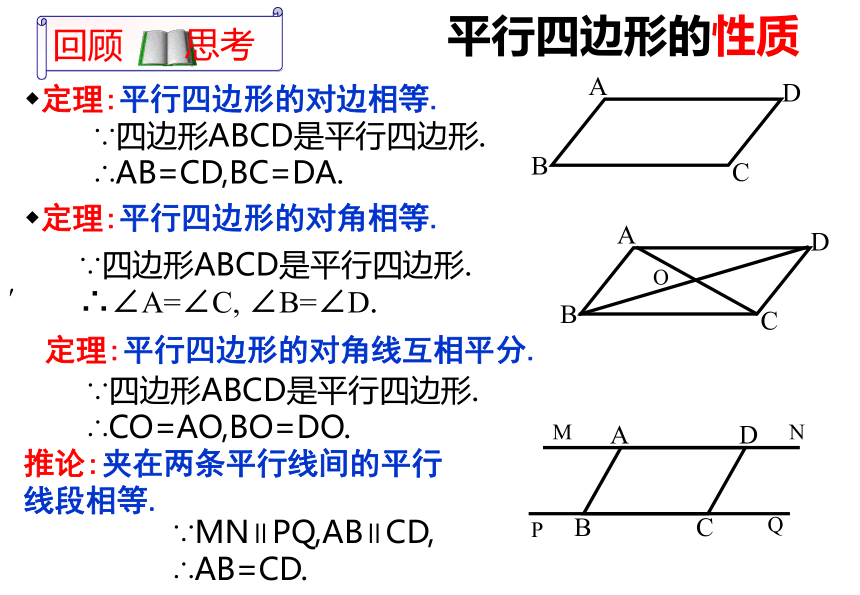
27.3平行四边形 平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形两组对边分别平行四边形四边形平行四边形平行四边形的性质定理:平行四边形的对边相等.′∵四边形ABCD是平行四边形.
∴AB=CD,BC=DA.定理:平行四边形的对角相等.∵四边形ABCD是平行四边形.
∴∠A=∠C, ∠B=∠D.定理:平行四边形的对角线互相平分.∵四边形ABCD是平行四边形.
∴CO=AO,BO=DO.推论:夹在两条平行线间的平行
线段相等.∵MN∥PQ,AB∥CD,
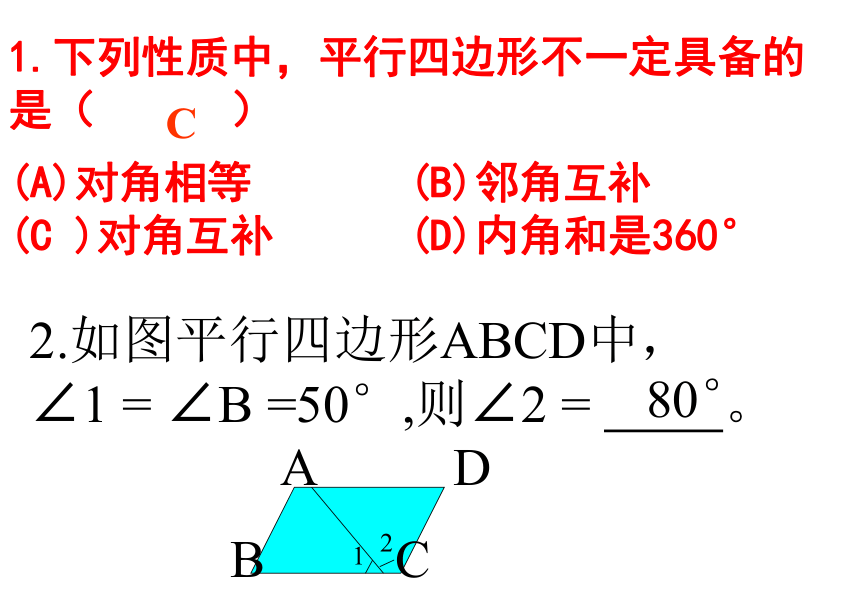
∴AB=CD.1.下列性质中,平行四边形不一定具备的
是( )(A)对角相等 (B)邻角互补
(C )对角互补 (D)内角和是360°C2.如图平行四边形ABCD中,
∠1 = ∠B =50°,则∠2 = 。80°ABCDO(1)50°30cm2(a+b)AD平行四边形的判定′定理:两组对边分别相等的四边形是平行四边形. 定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.定理:两组对角分别相等的四边形是平行四边形.∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.∵∠A=∠C,∠B=∠D.
∴四边形ABCD是平行四边形.例1:如图,四边形ABCD为平行四边形,延长BA至E,延长DC至F,使BE=DF,AF交BC于H,CE交AD于G.
求证:∠E=∠F证明:∵四边形ABCD是平行四边形BE=DF四边形AFCE是平行四边形注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F∴∴∴∴选择题:(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;下面判定四边形是平行四边形的方法
中,错误的是( )。(C )一组对边平行,一组对角相等;
( D)一组对边平行,另一组对边相等DF860°120°6cm, 8cm′ 2,已知:如图,在□ ABCD中,BF=DE.求证:四边形AFCE是平行四边形. 3、已知:如图,在□ ABCD中,∠ABC的平分线与AD相交于点P. 求证:PD+CD=BC.3分析:可过P点作PE∥DC交BC于E,对问题进行转化 4、如图,四边形ABCD与EBFD均是平行四边形.求证:AE=CF. 5、已知:如图, AC,BD是□ ABCD的两条对角线, AE⊥BD,CF⊥BD垂足分别是E,F.求证:AE=CF.6、如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且BE∥DF.
求证:∠1=∠2。 ′7、已知:如图.求证:四边形MNOP是平行四边形.分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.证明:∴四边形MNPO是平行四边形.平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形 谢 谢
用推理方法研究四边形
27.3平行四边形 平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形两组对边分别平行四边形四边形平行四边形平行四边形的性质定理:平行四边形的对边相等.′∵四边形ABCD是平行四边形.
∴AB=CD,BC=DA.定理:平行四边形的对角相等.∵四边形ABCD是平行四边形.
∴∠A=∠C, ∠B=∠D.定理:平行四边形的对角线互相平分.∵四边形ABCD是平行四边形.
∴CO=AO,BO=DO.推论:夹在两条平行线间的平行
线段相等.∵MN∥PQ,AB∥CD,
∴AB=CD.1.下列性质中,平行四边形不一定具备的
是( )(A)对角相等 (B)邻角互补
(C )对角互补 (D)内角和是360°C2.如图平行四边形ABCD中,
∠1 = ∠B =50°,则∠2 = 。80°ABCDO(1)50°30cm2(a+b)AD平行四边形的判定′定理:两组对边分别相等的四边形是平行四边形. 定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.定理:两组对角分别相等的四边形是平行四边形.∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.∵∠A=∠C,∠B=∠D.
∴四边形ABCD是平行四边形.例1:如图,四边形ABCD为平行四边形,延长BA至E,延长DC至F,使BE=DF,AF交BC于H,CE交AD于G.
求证:∠E=∠F证明:∵四边形ABCD是平行四边形BE=DF四边形AFCE是平行四边形注:利用平行四边形的性质来证明线段或角相等是一种常用方法。∠E=∠F∴∴∴∴选择题:(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;下面判定四边形是平行四边形的方法
中,错误的是( )。(C )一组对边平行,一组对角相等;
( D)一组对边平行,另一组对边相等DF860°120°6cm, 8cm′ 2,已知:如图,在□ ABCD中,BF=DE.求证:四边形AFCE是平行四边形. 3、已知:如图,在□ ABCD中,∠ABC的平分线与AD相交于点P. 求证:PD+CD=BC.3分析:可过P点作PE∥DC交BC于E,对问题进行转化 4、如图,四边形ABCD与EBFD均是平行四边形.求证:AE=CF. 5、已知:如图, AC,BD是□ ABCD的两条对角线, AE⊥BD,CF⊥BD垂足分别是E,F.求证:AE=CF.6、如图,在平行四边形ABCD中,E、F分别是AD、BC边上的点,且BE∥DF.
求证:∠1=∠2。 ′7、已知:如图.求证:四边形MNOP是平行四边形.分析:这是一道综合性题目,利用勾股定理,方程和平行四边形的判定进行计算性推理可获证.证明:∴四边形MNPO是平行四边形.平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形平行四边形 谢 谢
