圆柱的体积 解决问题(课件)六年级下册数学人教版(共15张PPT)
文档属性
| 名称 | 圆柱的体积 解决问题(课件)六年级下册数学人教版(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 827.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-01 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
圆柱的体积
---解决问题
人教版数学六年级下册
每到秋天,农民伯伯都要收许多玉米,为了便于晾晒和储存,他们用一些长方形的铁丝网片,作为粮食仓库。问题:
1、怎样做粮食仓库,有几种做法?
2、哪种方法储存的粮食更多?
1、用长方形的长做圆柱的底面周长
2、用长方形的宽做圆柱的底面周长
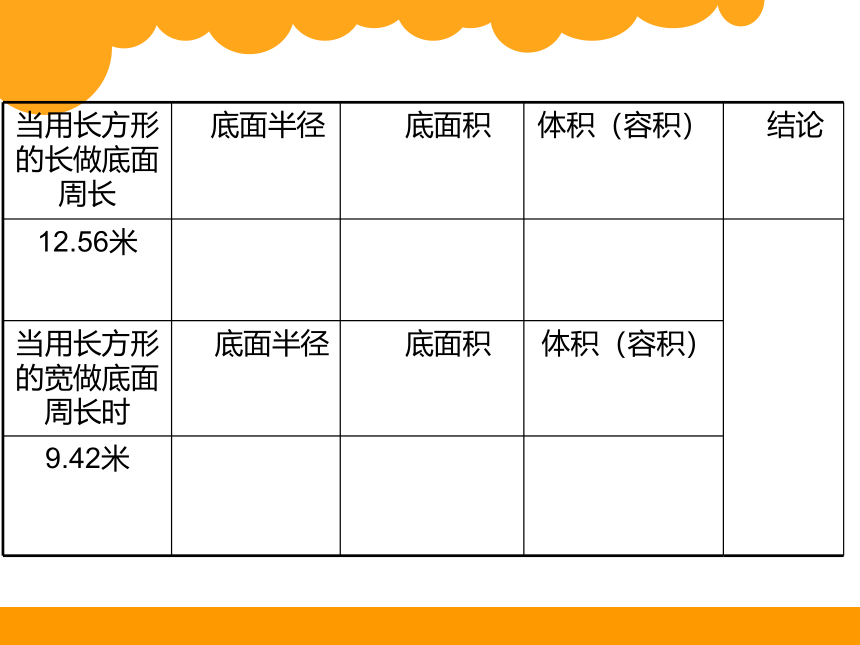
当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
12.56米
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
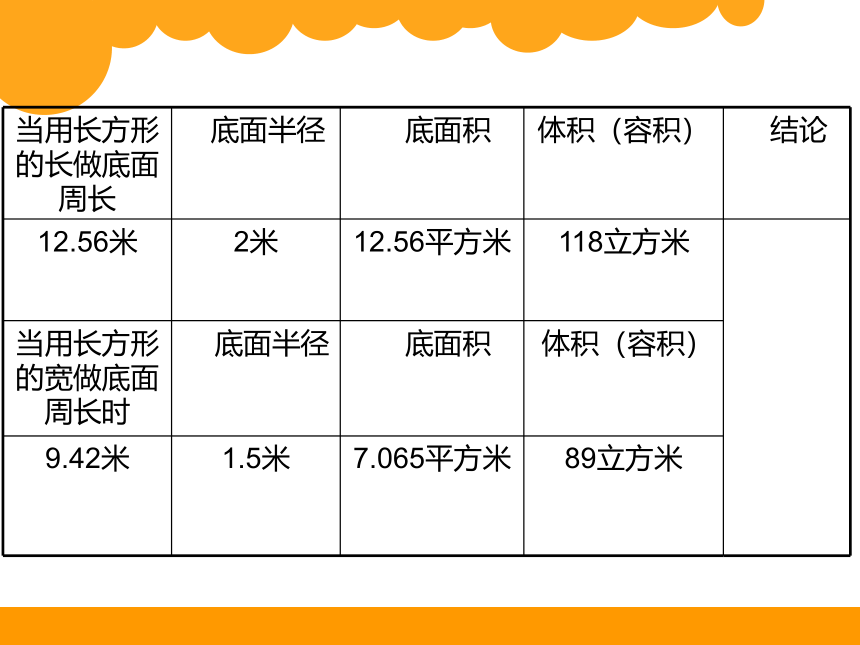
12.56米 2米 12.56平方米 118立方米
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 1.5米 7.065平方米 89立方米 当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
12.56米 2米 12.56平方米 118立方米 用长边做底面周长,短边做高,得到的体积大。
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 1.5米 7.065平方米 89立方米
实践应用:
有一堆18.84立方米的玉米,想用高为4米的铁丝网做成粮囤,铁丝网的长应是多少?
下面4个图形的面积都是36 dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现? (单位:dm)
第一个图
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个图
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
第三个图
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个图
3.14×(6÷3.14÷2)2×6≈17.20(dm3)
答:以18dm为圆柱的底面周长、2dm为高的圆柱体体积最大;以2dm为圆柱的底面周长、18dm为高的圆柱体体积最小。
发现:当圆柱的侧面积相同时,底面半径(或周长)大的体积就大。
谢 谢
圆柱的体积
---解决问题
人教版数学六年级下册
每到秋天,农民伯伯都要收许多玉米,为了便于晾晒和储存,他们用一些长方形的铁丝网片,作为粮食仓库。问题:
1、怎样做粮食仓库,有几种做法?
2、哪种方法储存的粮食更多?
1、用长方形的长做圆柱的底面周长
2、用长方形的宽做圆柱的底面周长
当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
12.56米
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
12.56米 2米 12.56平方米 118立方米
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 1.5米 7.065平方米 89立方米 当用长方形的长做底面周长 底面半径 底面积 体积(容积) 结论
12.56米 2米 12.56平方米 118立方米 用长边做底面周长,短边做高,得到的体积大。
当用长方形的宽做底面周长时 底面半径 底面积 体积(容积) 9.42米 1.5米 7.065平方米 89立方米
实践应用:
有一堆18.84立方米的玉米,想用高为4米的铁丝网做成粮囤,铁丝网的长应是多少?
下面4个图形的面积都是36 dm2。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现? (单位:dm)
第一个图
3.14×(18÷3.14÷2)2×2≈51.59(dm3)
或3.14×(2÷3.14÷2)2×18≈5.73(dm3)
第二个图
3.14×(12÷3.14÷2)2×3≈34.39(dm3)
或3.14×(3÷3.14÷2)2×12≈8.60(dm3)
第三个图
3.14×(9÷3.14÷2)2×4≈25.80(dm3)
或3.14×(4÷3.14÷2)2×9≈11.46(dm3)
第四个图
3.14×(6÷3.14÷2)2×6≈17.20(dm3)
答:以18dm为圆柱的底面周长、2dm为高的圆柱体体积最大;以2dm为圆柱的底面周长、18dm为高的圆柱体体积最小。
发现:当圆柱的侧面积相同时,底面半径(或周长)大的体积就大。
谢 谢
