沪科版七年级数学下册 第八章整式乘法与因式分解单元自测题(含解析)
文档属性
| 名称 | 沪科版七年级数学下册 第八章整式乘法与因式分解单元自测题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 228.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 20:56:51 | ||
图片预览




文档简介
沪科版七年级数学下册第八章整式乘法与因式分解 单元自测题
一、单选题
1.下列运算正确的是( )
A. B. C. D.
2.计算:(﹣a2b)2 a2=( )
A.a4b2 B.a6b2 C.a5b2 D.a8b2
3.下列不能用平方差公式计算的是( )
A. B.
C. D.
4.下列等式从左到右的变形是因式分解的是( )
A. B.
C. D.
5.若,,则( )
A.18 B.8 C.11 D.6
6.(x+5)(x-3)等于( )
A.x2 -15 B.x2 + 15
C.x2 + 2x -15 D.x2 - 2x - 15
7.要使多项式不含的一次项,则( )
A. B. C. D.
8.下列运算正确的是( )
A. B.
C. D.
9.若多项式x2+px+q因式分解的结果为(x+5)(x-4),则p+q的值为( )
A.-19 B.-20 C.1 D.9
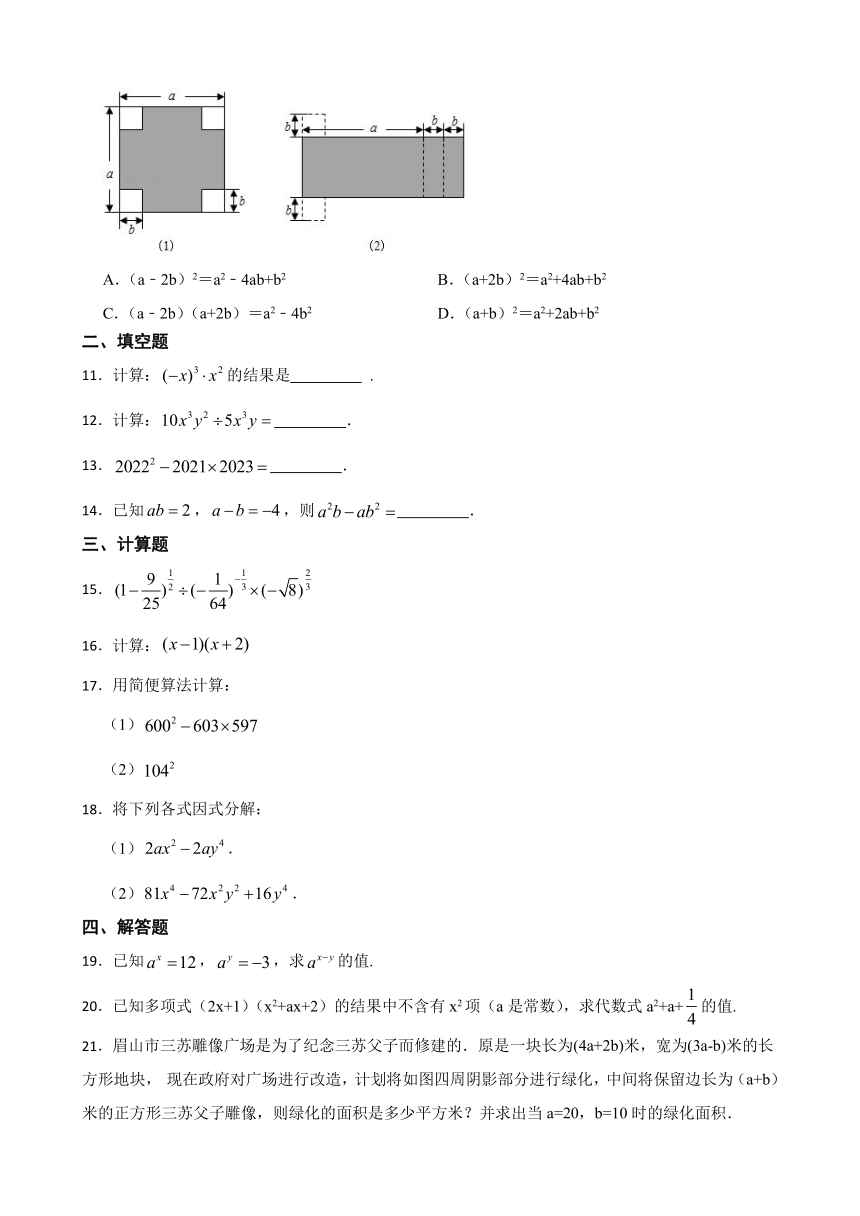
10.如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a﹣2b)2=a2﹣4ab+b2 B.(a+2b)2=a2+4ab+b2
C.(a﹣2b)(a+2b)=a2﹣4b2 D.(a+b)2=a2+2ab+b2
二、填空题
11.计算:的结果是 .
12.计算: .
13. .
14.已知,,则 .
三、计算题
15.
16.计算:
17.用简便算法计算:
(1)
(2)
18.将下列各式因式分解:
(1).
(2).
四、解答题
19.已知,,求的值.
20.已知多项式(2x+1)(x2+ax+2)的结果中不含有x2项(a是常数),求代数式a2+a+的值.
21.眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
五、综合题
22.甲、乙两人共同计算一道整式:,由于甲抄错了a的符号,得到的结果是,乙漏抄了第二个多项式中x的系数,得到的结果是.
(1)求的值;
(2)若整式中的a的符号不抄错,且,请计算这道题的符合题意结果.
23.阅读下列材料:
因式分解的常用方法有提公因式法和公式法,但有的多项式仅用上述方法就无法分解,如.我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,
过程如下:
.
这种因式分解的方法叫分组分解法.
利用这种分组的思想方法解决下列问题:
(1)因式分解:;
(2)因式分解:.
答案解析部分
1.【答案】C
【解析】【解答】解:A、a3与a2不是同类项,不能合并,故此项错误;
B、x2·x3=x5,故此项错误;
C、 ,故此项正确;
D、 ,故此项错误;
故答案为:C.
【分析】根据合并同类项、同底数幂的乘法、幂的乘方分别计算,再判断即可.
2.【答案】B
【解析】【解答】解: (﹣a2b)2 a2
=a4b2 a2
=a4+2b2
=a6b2,
故答案为:B.
【分析】先进行积的乘方的运算,再进行单项式乘单项式的运算,即可解答.
3.【答案】B
【解析】【解答】解:A.,能用平方差公式计算,不符合题意;
B.,不能用平方差公式计算,符合题意;
C.,能用平方差公式计算,不符合题意;
D.,能用平方差公式计算,不符合题意.
故答案为:B.
【分析】利用平方差公式的计算方法逐项判断即可。
4.【答案】C
【解析】【解答】A.等式的左边不是多项式,不属于因式分解,故本选项不合题意; .
B.从左边到右边的变形是整式乘法,不属于因式分解,故本选项不符合题意;
C.从左边到右边的变形属于因式分解,故本选项符合题意;
D.y2- 2xy+ y=y(y- 2x+ 1),故本选项不符合题意;
故答案为:C.
【分析】根据因式分解的定义:将和差的形式变成乘积的形式逐项判断即可。
5.【答案】A
【解析】【解答】解:∵am=2,an=3,
∴am+2n=am×a2n=am×(an)2=2×32=18.
故答案为:A.
【分析】由同底数幂的乘法的逆用及幂的乘方运算法则的逆用将待求式子变形为am×(an)2,然后整体代入按含乘方的有理数的混合运算的运算顺序计算即可.
6.【答案】C
【解析】【解答】解:,
故答案为:C.
【分析】利用多项式乘多项式的计算方法求解即可。
7.【答案】B
【解析】【解答】解:,
由结果不含x的一次项,得到,
解得:,
故答案为:B.
【分析】根据多项式乘多项式法则“多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得积相加”可将多项式化简,再根据多项式不含x的一次项可得关于q的方程:q+1=0,解方程可求解.
8.【答案】B
【解析】【解答】解:A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意;
故答案为:B.
【分析】利用同底数幂的乘法、幂的乘方、积的乘方、完全平方公式及单项式除以单项式逐项判断即可。
9.【答案】A
【解析】【解答】解:∵(x+5)(x-4) =x2-4x+5x-20=x2+x-20
而x2+px+q因式分解的结果为(x+5)(x-4),
∴x2+px+q=x2+x-20,
∴p=1,q=-20,
∴p+q=1+(-20)=-19.
故答案为:A.
【分析】首先利用多项式乘以多形式的法则求出(x+5)(x-4)的积,进而根据因式分解的定义可得x2+px+q=x2+x-20,由多项式的性质得p、q的值,最后再求p、q的和即可.
10.【答案】C
【解析】【解答】解:图(1)中阴影部分的面积为:a2-4b2,
图(2)中阴影部分的面积为:(a-2b)(a+2b),
∴(a-2b)(a+2b)=a2-4b2.
故答案为:C.
【分析】用边长为a的大正方形的面积减去4个边长为b的小正方形的面积可表示出图(1)的面积,图(2)是一个长为(a+2b),宽为(a-2b)的矩形,根据矩形面积计算公式表示出图(2)的面积,进而根据两个图形面积相等即可得出答案.
11.【答案】
【解析】【解答】解:
.
故答案为:.
【分析】同底数幂相乘,底数不变,指数相加,据此计算.
12.【答案】2y
【解析】【解答】解:.
故答案为:.
【分析】根据单项式除以单项式法则进行解答即可.
13.【答案】1
【解析】【解答】原式==,
故答案为:1.
【分析】将代数式变形为,再计算即可。
14.【答案】﹣8
【解析】【解答】解:∵,,
∴
故答案为:-8.
【分析】对待求式进行分解可得ab(a-b),然后将已知条件代入进行计算.
15.【答案】解:
【解析】【分析】根据分数指数幂的运算性质可得原式=,结合幂的乘方法则可得,然后根据有理数的乘法法则进行计算.
16.【答案】解:原式=x2+2x-x-2
=x2+x-2.
【解析】【分析】利用多项式乘以多项式法则计算求解即可。
17.【答案】(1)解:
(2)解:
【解析】【分析】(1)原式可变形为6002-(600+3)×(600-3),然后利用平方差公式进行计算;
(2)原式可变形为(100+4)2,然后利用完全平方公式进行计算.
18.【答案】(1)解:
;
(2)解:
.
【解析】【分析】(1)先提取公因式2a,再利用平方差公式继续分解因式,即可得出结果;
(2)先根据完全平方公式分解因式,再利用平方差公式继续分解因式,即可得出结果.
19.【答案】解:∵,,
∴.
【解析】【分析】根据同底数幂的除法法则可得ax-y=ax÷ay,然后将已知条件代入进行计算.
20.【答案】解:(2x+1)(x2+ax+2)
=2x3+2ax2+4x+x2+ax+2
=2x3+(2a+1)x2+(4+a)x+2,
∵不含有x2项,
∴2a+1=0,
∴a=-,
当a=-时,
原式=(-)2-+
=-+
=0.
【解析】【分析】利用多项式乘多项式法则将原式展开,由于结果中不含有x2项,可得二次项系数和为0,据此求出a值,再代入计算即可.
21.【答案】解:由题意得:绿化的面积为:(4a+2b)(3a b) (a+b)2=12a2 4ab+6ab 2b2 (a2+2ab+b2)=12a2+2ab 2b2 a2 2ab b2=11a2 3b2
当a=20,b=10时,
原式=11×202 3×102=4400 300=4100.
【解析】【分析】 绿化的面积=长方形的面积-空白正方形的面积,据此列式,再利用整式的混合运算将原式化简,最后将a、b值代入计算即可.
22.【答案】(1)解:甲抄错了a的符号的计算结果为:,
因为对应的系数相等,故,
乙漏抄了第二个多项式中x的系数,计算结果为:.
因为对应的系数相等,故,,
∴
(2)解:乙漏抄了第二个多项式中x的系数,得到的结果得出:
,
故,
∴b=-1,
把a=3,b=-1代入,
得(x+3)(2x-1)=2x2+5x-3,
故答案为:2x2+5x-3.
【解析】【分析】(1)利用多项式乘多项式的计算方法展开,再利用待定系法可得答案;
(2)先求出b的值,再将a、b的值代入计算即可。
23.【答案】(1)解:,
,
,
;
(2)解:,
,
,
.
【解析】【分析】 (1)前三项符合完全平方公式,再和最后一项用平方差公式;
(2)前两项和后两项分别分解因式。
一、单选题
1.下列运算正确的是( )
A. B. C. D.
2.计算:(﹣a2b)2 a2=( )
A.a4b2 B.a6b2 C.a5b2 D.a8b2
3.下列不能用平方差公式计算的是( )
A. B.
C. D.
4.下列等式从左到右的变形是因式分解的是( )
A. B.
C. D.
5.若,,则( )
A.18 B.8 C.11 D.6
6.(x+5)(x-3)等于( )
A.x2 -15 B.x2 + 15
C.x2 + 2x -15 D.x2 - 2x - 15
7.要使多项式不含的一次项,则( )
A. B. C. D.
8.下列运算正确的是( )
A. B.
C. D.
9.若多项式x2+px+q因式分解的结果为(x+5)(x-4),则p+q的值为( )
A.-19 B.-20 C.1 D.9
10.如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a﹣2b)2=a2﹣4ab+b2 B.(a+2b)2=a2+4ab+b2
C.(a﹣2b)(a+2b)=a2﹣4b2 D.(a+b)2=a2+2ab+b2
二、填空题
11.计算:的结果是 .
12.计算: .
13. .
14.已知,,则 .
三、计算题
15.
16.计算:
17.用简便算法计算:
(1)
(2)
18.将下列各式因式分解:
(1).
(2).
四、解答题
19.已知,,求的值.
20.已知多项式(2x+1)(x2+ax+2)的结果中不含有x2项(a是常数),求代数式a2+a+的值.
21.眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
五、综合题
22.甲、乙两人共同计算一道整式:,由于甲抄错了a的符号,得到的结果是,乙漏抄了第二个多项式中x的系数,得到的结果是.
(1)求的值;
(2)若整式中的a的符号不抄错,且,请计算这道题的符合题意结果.
23.阅读下列材料:
因式分解的常用方法有提公因式法和公式法,但有的多项式仅用上述方法就无法分解,如.我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,
过程如下:
.
这种因式分解的方法叫分组分解法.
利用这种分组的思想方法解决下列问题:
(1)因式分解:;
(2)因式分解:.
答案解析部分
1.【答案】C
【解析】【解答】解:A、a3与a2不是同类项,不能合并,故此项错误;
B、x2·x3=x5,故此项错误;
C、 ,故此项正确;
D、 ,故此项错误;
故答案为:C.
【分析】根据合并同类项、同底数幂的乘法、幂的乘方分别计算,再判断即可.
2.【答案】B
【解析】【解答】解: (﹣a2b)2 a2
=a4b2 a2
=a4+2b2
=a6b2,
故答案为:B.
【分析】先进行积的乘方的运算,再进行单项式乘单项式的运算,即可解答.
3.【答案】B
【解析】【解答】解:A.,能用平方差公式计算,不符合题意;
B.,不能用平方差公式计算,符合题意;
C.,能用平方差公式计算,不符合题意;
D.,能用平方差公式计算,不符合题意.
故答案为:B.
【分析】利用平方差公式的计算方法逐项判断即可。
4.【答案】C
【解析】【解答】A.等式的左边不是多项式,不属于因式分解,故本选项不合题意; .
B.从左边到右边的变形是整式乘法,不属于因式分解,故本选项不符合题意;
C.从左边到右边的变形属于因式分解,故本选项符合题意;
D.y2- 2xy+ y=y(y- 2x+ 1),故本选项不符合题意;
故答案为:C.
【分析】根据因式分解的定义:将和差的形式变成乘积的形式逐项判断即可。
5.【答案】A
【解析】【解答】解:∵am=2,an=3,
∴am+2n=am×a2n=am×(an)2=2×32=18.
故答案为:A.
【分析】由同底数幂的乘法的逆用及幂的乘方运算法则的逆用将待求式子变形为am×(an)2,然后整体代入按含乘方的有理数的混合运算的运算顺序计算即可.
6.【答案】C
【解析】【解答】解:,
故答案为:C.
【分析】利用多项式乘多项式的计算方法求解即可。
7.【答案】B
【解析】【解答】解:,
由结果不含x的一次项,得到,
解得:,
故答案为:B.
【分析】根据多项式乘多项式法则“多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得积相加”可将多项式化简,再根据多项式不含x的一次项可得关于q的方程:q+1=0,解方程可求解.
8.【答案】B
【解析】【解答】解:A. ,不符合题意;
B. ,符合题意;
C. ,不符合题意;
D. ,不符合题意;
故答案为:B.
【分析】利用同底数幂的乘法、幂的乘方、积的乘方、完全平方公式及单项式除以单项式逐项判断即可。
9.【答案】A
【解析】【解答】解:∵(x+5)(x-4) =x2-4x+5x-20=x2+x-20
而x2+px+q因式分解的结果为(x+5)(x-4),
∴x2+px+q=x2+x-20,
∴p=1,q=-20,
∴p+q=1+(-20)=-19.
故答案为:A.
【分析】首先利用多项式乘以多形式的法则求出(x+5)(x-4)的积,进而根据因式分解的定义可得x2+px+q=x2+x-20,由多项式的性质得p、q的值,最后再求p、q的和即可.
10.【答案】C
【解析】【解答】解:图(1)中阴影部分的面积为:a2-4b2,
图(2)中阴影部分的面积为:(a-2b)(a+2b),
∴(a-2b)(a+2b)=a2-4b2.
故答案为:C.
【分析】用边长为a的大正方形的面积减去4个边长为b的小正方形的面积可表示出图(1)的面积,图(2)是一个长为(a+2b),宽为(a-2b)的矩形,根据矩形面积计算公式表示出图(2)的面积,进而根据两个图形面积相等即可得出答案.
11.【答案】
【解析】【解答】解:
.
故答案为:.
【分析】同底数幂相乘,底数不变,指数相加,据此计算.
12.【答案】2y
【解析】【解答】解:.
故答案为:.
【分析】根据单项式除以单项式法则进行解答即可.
13.【答案】1
【解析】【解答】原式==,
故答案为:1.
【分析】将代数式变形为,再计算即可。
14.【答案】﹣8
【解析】【解答】解:∵,,
∴
故答案为:-8.
【分析】对待求式进行分解可得ab(a-b),然后将已知条件代入进行计算.
15.【答案】解:
【解析】【分析】根据分数指数幂的运算性质可得原式=,结合幂的乘方法则可得,然后根据有理数的乘法法则进行计算.
16.【答案】解:原式=x2+2x-x-2
=x2+x-2.
【解析】【分析】利用多项式乘以多项式法则计算求解即可。
17.【答案】(1)解:
(2)解:
【解析】【分析】(1)原式可变形为6002-(600+3)×(600-3),然后利用平方差公式进行计算;
(2)原式可变形为(100+4)2,然后利用完全平方公式进行计算.
18.【答案】(1)解:
;
(2)解:
.
【解析】【分析】(1)先提取公因式2a,再利用平方差公式继续分解因式,即可得出结果;
(2)先根据完全平方公式分解因式,再利用平方差公式继续分解因式,即可得出结果.
19.【答案】解:∵,,
∴.
【解析】【分析】根据同底数幂的除法法则可得ax-y=ax÷ay,然后将已知条件代入进行计算.
20.【答案】解:(2x+1)(x2+ax+2)
=2x3+2ax2+4x+x2+ax+2
=2x3+(2a+1)x2+(4+a)x+2,
∵不含有x2项,
∴2a+1=0,
∴a=-,
当a=-时,
原式=(-)2-+
=-+
=0.
【解析】【分析】利用多项式乘多项式法则将原式展开,由于结果中不含有x2项,可得二次项系数和为0,据此求出a值,再代入计算即可.
21.【答案】解:由题意得:绿化的面积为:(4a+2b)(3a b) (a+b)2=12a2 4ab+6ab 2b2 (a2+2ab+b2)=12a2+2ab 2b2 a2 2ab b2=11a2 3b2
当a=20,b=10时,
原式=11×202 3×102=4400 300=4100.
【解析】【分析】 绿化的面积=长方形的面积-空白正方形的面积,据此列式,再利用整式的混合运算将原式化简,最后将a、b值代入计算即可.
22.【答案】(1)解:甲抄错了a的符号的计算结果为:,
因为对应的系数相等,故,
乙漏抄了第二个多项式中x的系数,计算结果为:.
因为对应的系数相等,故,,
∴
(2)解:乙漏抄了第二个多项式中x的系数,得到的结果得出:
,
故,
∴b=-1,
把a=3,b=-1代入,
得(x+3)(2x-1)=2x2+5x-3,
故答案为:2x2+5x-3.
【解析】【分析】(1)利用多项式乘多项式的计算方法展开,再利用待定系法可得答案;
(2)先求出b的值,再将a、b的值代入计算即可。
23.【答案】(1)解:,
,
,
;
(2)解:,
,
,
.
【解析】【分析】 (1)前三项符合完全平方公式,再和最后一项用平方差公式;
(2)前两项和后两项分别分解因式。
