9.2.1总体取值规律的估计 课件(共31张PPT)
文档属性
| 名称 | 9.2.1总体取值规律的估计 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 02:36:44 | ||
图片预览






文档简介
(共31张PPT)
人教版 数学 必修 第二册
9.2.1 总体取值规律的估计
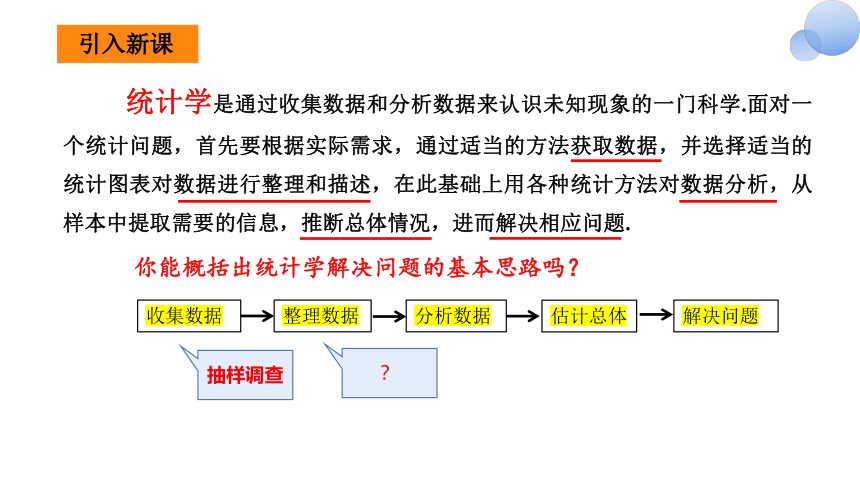
引入新课
统计学是通过收集数据和分析数据来认识未知现象的一门科学.面对一个统计问题,首先要根据实际需求,通过适当的方法获取数据,并选择适当的统计图表对数据进行整理和描述,在此基础上用各种统计方法对数据分析,从样本中提取需要的信息,推断总体情况,进而解决相应问题.
你能概括出统计学解决问题的基本思路吗?
收集数据
整理数据
分析数据
估计总体
解决问题
抽样调查
?
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一个居民月均水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
如果希望大多数居民生活不受影响,那么标准a定为多少比较合适呢?
实际情景
问题1 为了较为合理地确定出这个标准,需要做哪些工作?
为了制定一个较为合理的标准a,必须先了解全市所有居民月均用水量在不同范围内居民用户所占比例.
问题2 为了了解全市居民月均用水量数据,采用什么方法去调查呢?
采用抽样调查的方式,通过分析样本数据来估计全市居民月均用水量的分布情况.
问题提出
问题3 在这个问题中,抽样总体,个体,调查变量分别是什么呢?
抽样总体是该市的全体居民用户,个体是每户居民用户,调查变量是居民用户的月均用水量.
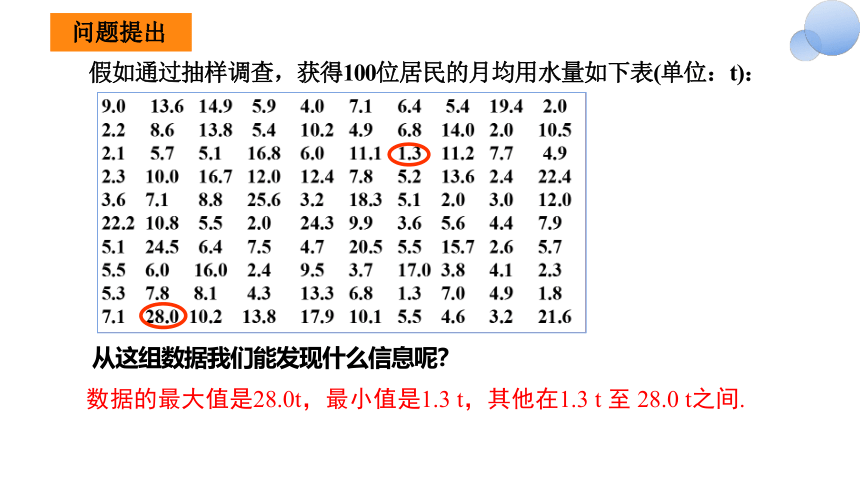
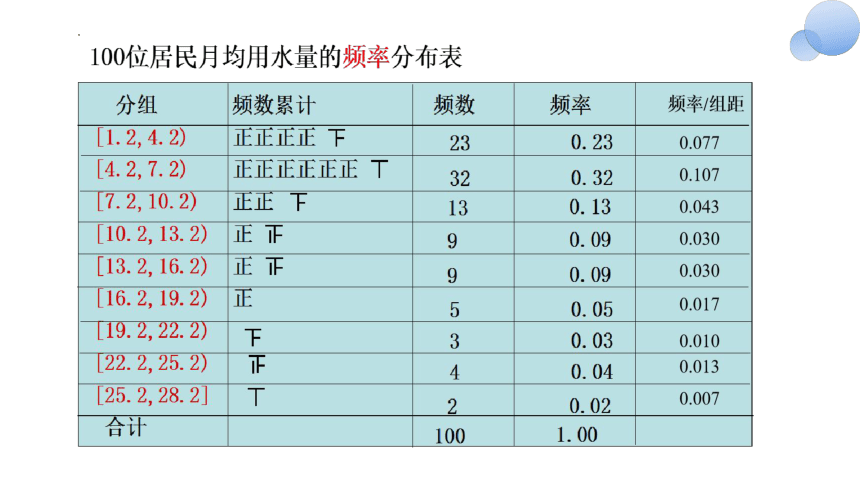
假如通过抽样调查,获得100位居民的月均用水量如下表(单位:t):
从这组数据我们能发现什么信息呢?
数据的最大值是28.0t,最小值是1.3 t,其他在1.3 t 至 28.0 t之间.
问题提出
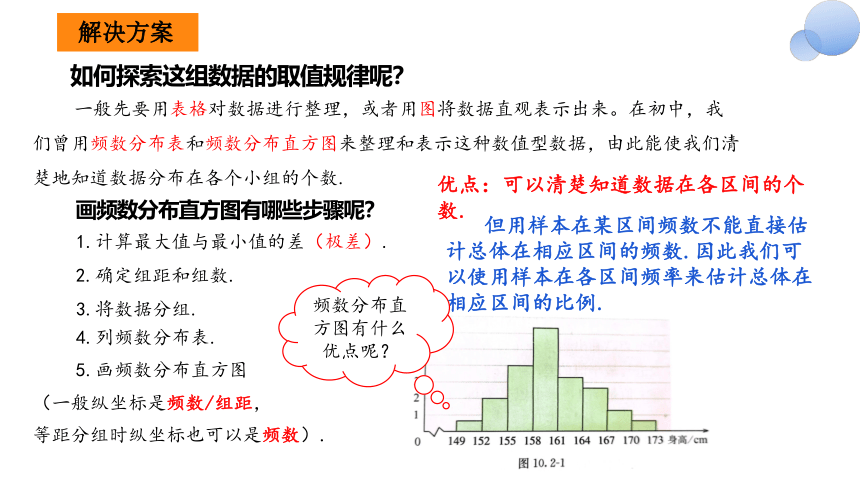
一般先要用表格对数据进行整理,或者用图将数据直观表示出来。在初中,我们曾用频数分布表和频数分布直方图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
解决方案
如何探索这组数据的取值规律呢?
画频数分布直方图有哪些步骤呢?
1.计算最大值与最小值的差(极差).
2.确定组距和组数.
3.将数据分组.
4.列频数分布表.
5.画频数分布直方图
(一般纵坐标是频数/组距,
等距分组时纵坐标也可以是频数).
优点:可以清楚知道数据在各区间的个数.
但用样本在某区间频数不能直接估计总体在相应区间的频数.因此我们可以使用样本在各区间频率来估计总体在相应区间的比例.
频数分布直方图有什么优点呢?
画图方法
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民占全市居民用户的比例,所以选择频率分布表和频率分布直方图在整理和表示数据。
画频率分布直方图步骤:
1.计算最大值与最小值的差(极差).
2.确定组距和组数(当样本数量不超过100时,常分成5 12组,一般取等长组距,组距力求取整).
3.将数据分组(分组时要使第一组左端点略小于最小值,最后一组右端点略大于最大值).
4.列 分布表.
5.画 分布直方图(一般纵坐标是 /组距).
频率
频数
频数
频率
频率
频数
样本的频率分布直方图
第一步 求极差
极差为一组数据中最大值与最小值的差,样本观测数据的最大值是28.0 t,最小值是1.3 t,极差为:
28.0-1.3=26.7
第二步 决定组距和组数
(当样本数量不超过100时,常分成5~12组,一般取等长组距,组距力求取整.组距组数也没有固定标准,需要根据实际情况和经验进行尝试.)
如果取所有组距为3,那么数据可以共分为多少组?
可以将数据分为9组.
如果取所有组距为4,那么数据可以共分为多少组?
可以将数据分为7组.
第三步 将数据分组
问题:以组距为3进行分组,上述100个数据共分为9组,各组数据的取值范围可以如何设定?
[1.2,4.2),[4.2,7.2),…,[25.2,28.2]
第四步 列频率分布表
频率分布表一般由四列组成:分组,频数累计,频数,频率,如何计算频率呢?
第五步 画频率分布直方图
横轴表示月均用水量,纵轴表示
(分组时要使第一组左端点略小于最小值,最后一组右端点略大于最大值).
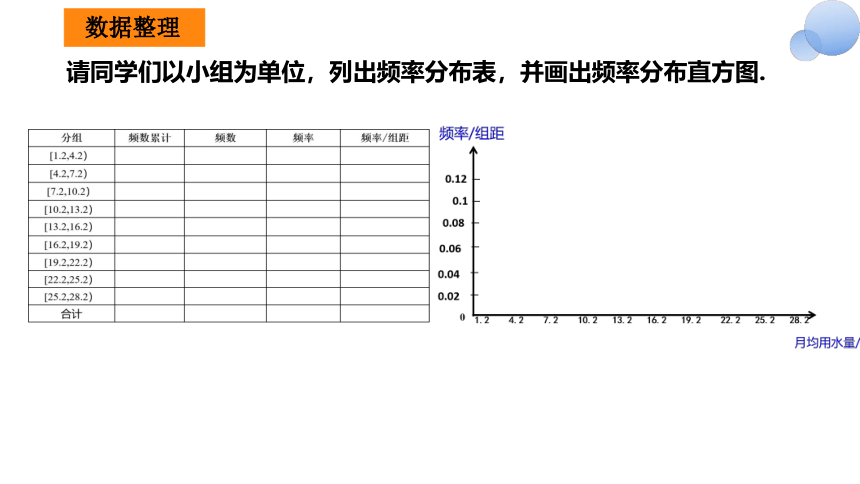
请同学们以小组为单位,列出频率分布表,并画出频率分布直方图.
数据整理
0.077
0.077
0.077
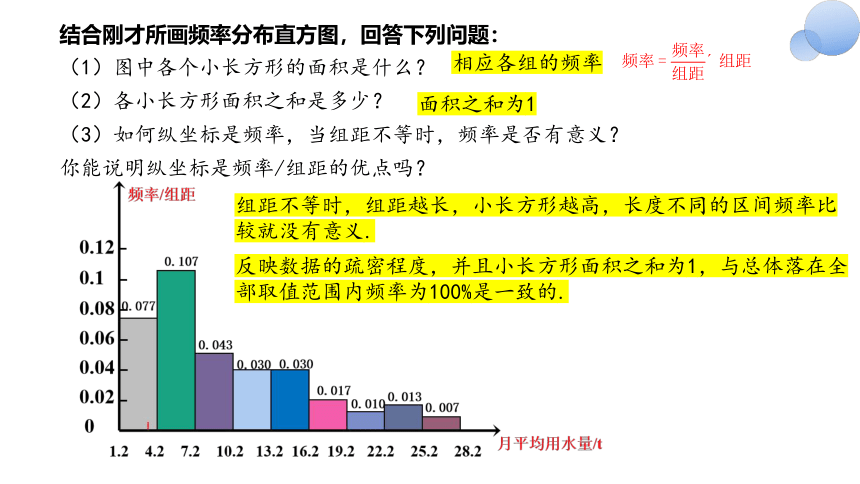
结合刚才所画频率分布直方图,回答下列问题:
(1)图中各个小长方形的面积是什么?
(2)各小长方形面积之和是多少?
(3)如何纵坐标是频率,当组距不等时,频率是否有意义?你能说明纵坐标是频率/组距的优点吗?
相应各组的频率
面积之和为1
组距不等时,组距越长,小长方形越高,长度不同的区间频率比较就没有意义.
反映数据的疏密程度,并且小长方形面积之和为1,与总体落在全部取值范围内频率为100%是一致的.
观察表9.2-1和图9.2-1,你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
观察表9.2-1你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
数据分析
(1)从频率分布表中可以看出,样本观测数据落在各个小组的比例大小.
例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小,等等.
数据分析
观察图9.2-1你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
(2)从频率分布直方图能直观地表明数据分布的形状和总体趋势.可以看出,数据的分布不对称,图形左边高、右边低,右边有一个较长的“尾巴”。这表明大部分居民用户的月均用水量集中在一个较低值区域,尤其在[1.2,7.2)最为集中,少数用户居民的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
根据100户居民用户的月均用水量的频率分布,可以推测该市全体居民用户月均用水量也会有类似的分布,即大部分居民用户月均用水量集中在较低值区域.
规律总结
你能根据样本观测数据的频率分布,估计总体的取值规律吗?
我们利用样本观测数据对整体情况的估计一定准确吗?
这使我们确定用水量标准时,可以定一个合适的值,以达到既不影响大多数居民用户的水费支出,又能节水的目的.
由于样本的随机性,这种估计可能会存在一定误差,但这一误差一般不会影响我们对总体分布情况的大致了解.
除了样本的随机性,还有哪些因素会影响人们对整体的判断呢?
组数为3
组数为5
组数为9
组数为13
组数为16
组数为24
组数为27
探究 分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分布直方图(9.2-2).观察图形,你发现不同的组数对于直方图呈现数据分布规律有什么影响?
组数少、组距大:易看出数据整体的分布特点,无法看出每组内的数据分布情况,损失了较多的原始数据信息;
组数多、组距小:保留较多原始数据信息;但小长方形较多,有时图形会变得不规则,不容易从中看出总体分布特点;
直方图会依赖样本数据,稳定性差.
1. 从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在50~350 kW h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示.
(1) 直方图中x的值为________;
(2) 在被调查的用户中,用电量落在区间[100,250) 内的户数为_____.
70
0.0044
课堂练习
(1)由频率分布直方图中各小长方形的总面积为1,
得(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2+x)×50=1,
得x=0.004 4.
(2)用电量在[100,250)内的频率为
(0.003 6+0.006 0+0.004 4)×50=0.7,
因此用电量在区间[100,250)内的户数为0.7×100=70.
解:(1) 通话时长在区间[15,20),[20,30)内的次数分别为9次和12次.
(2) 区间[20,30)内的通话次数 少于区间[15,20内的通话次数.
2.如图,胡晓统计了他爸爸9月的手机通话明细清单,发现他爸爸该月共通话60次. 胡晓按每次通话时间长短进行分组(每组为左闭右开的区间),画出了频率分布直方图.
(1) 通话时长在区间[15,20),[20,30) 内的次数分别为多少
(2) 区间[20, 30)上的小长方形高度低于[15, 20)上的小长方形的高度,说明什么
课堂练习
课堂小结
通过本节课的学习你收获了哪些知识?掌握了哪些方法?体会了哪些思想呢?
课堂小结
本节课我们了解了统计学解决问题的基本思路,研究了列频率分布表、画频率分布直方图的方法,并利用图表整理数据,分析样本数据取值规律,并借助样本数据取值规律对总体数据取值规律进行估计.提升数学运算、数据分析素养,不同分组方法也会影响对总体的判断,因此要注意积累数据分组、合理使用图表的经验.
布置作业
2.课本199第3题.
谢谢聆听!
人教版 数学 必修 第二册
9.2.1 总体取值规律的估计
引入新课
统计学是通过收集数据和分析数据来认识未知现象的一门科学.面对一个统计问题,首先要根据实际需求,通过适当的方法获取数据,并选择适当的统计图表对数据进行整理和描述,在此基础上用各种统计方法对数据分析,从样本中提取需要的信息,推断总体情况,进而解决相应问题.
你能概括出统计学解决问题的基本思路吗?
收集数据
整理数据
分析数据
估计总体
解决问题
抽样调查
?
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一个居民月均水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
如果希望大多数居民生活不受影响,那么标准a定为多少比较合适呢?
实际情景
问题1 为了较为合理地确定出这个标准,需要做哪些工作?
为了制定一个较为合理的标准a,必须先了解全市所有居民月均用水量在不同范围内居民用户所占比例.
问题2 为了了解全市居民月均用水量数据,采用什么方法去调查呢?
采用抽样调查的方式,通过分析样本数据来估计全市居民月均用水量的分布情况.
问题提出
问题3 在这个问题中,抽样总体,个体,调查变量分别是什么呢?
抽样总体是该市的全体居民用户,个体是每户居民用户,调查变量是居民用户的月均用水量.
假如通过抽样调查,获得100位居民的月均用水量如下表(单位:t):
从这组数据我们能发现什么信息呢?
数据的最大值是28.0t,最小值是1.3 t,其他在1.3 t 至 28.0 t之间.
问题提出
一般先要用表格对数据进行整理,或者用图将数据直观表示出来。在初中,我们曾用频数分布表和频数分布直方图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
解决方案
如何探索这组数据的取值规律呢?
画频数分布直方图有哪些步骤呢?
1.计算最大值与最小值的差(极差).
2.确定组距和组数.
3.将数据分组.
4.列频数分布表.
5.画频数分布直方图
(一般纵坐标是频数/组距,
等距分组时纵坐标也可以是频数).
优点:可以清楚知道数据在各区间的个数.
但用样本在某区间频数不能直接估计总体在相应区间的频数.因此我们可以使用样本在各区间频率来估计总体在相应区间的比例.
频数分布直方图有什么优点呢?
画图方法
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民占全市居民用户的比例,所以选择频率分布表和频率分布直方图在整理和表示数据。
画频率分布直方图步骤:
1.计算最大值与最小值的差(极差).
2.确定组距和组数(当样本数量不超过100时,常分成5 12组,一般取等长组距,组距力求取整).
3.将数据分组(分组时要使第一组左端点略小于最小值,最后一组右端点略大于最大值).
4.列 分布表.
5.画 分布直方图(一般纵坐标是 /组距).
频率
频数
频数
频率
频率
频数
样本的频率分布直方图
第一步 求极差
极差为一组数据中最大值与最小值的差,样本观测数据的最大值是28.0 t,最小值是1.3 t,极差为:
28.0-1.3=26.7
第二步 决定组距和组数
(当样本数量不超过100时,常分成5~12组,一般取等长组距,组距力求取整.组距组数也没有固定标准,需要根据实际情况和经验进行尝试.)
如果取所有组距为3,那么数据可以共分为多少组?
可以将数据分为9组.
如果取所有组距为4,那么数据可以共分为多少组?
可以将数据分为7组.
第三步 将数据分组
问题:以组距为3进行分组,上述100个数据共分为9组,各组数据的取值范围可以如何设定?
[1.2,4.2),[4.2,7.2),…,[25.2,28.2]
第四步 列频率分布表
频率分布表一般由四列组成:分组,频数累计,频数,频率,如何计算频率呢?
第五步 画频率分布直方图
横轴表示月均用水量,纵轴表示
(分组时要使第一组左端点略小于最小值,最后一组右端点略大于最大值).
请同学们以小组为单位,列出频率分布表,并画出频率分布直方图.
数据整理
0.077
0.077
0.077
结合刚才所画频率分布直方图,回答下列问题:
(1)图中各个小长方形的面积是什么?
(2)各小长方形面积之和是多少?
(3)如何纵坐标是频率,当组距不等时,频率是否有意义?你能说明纵坐标是频率/组距的优点吗?
相应各组的频率
面积之和为1
组距不等时,组距越长,小长方形越高,长度不同的区间频率比较就没有意义.
反映数据的疏密程度,并且小长方形面积之和为1,与总体落在全部取值范围内频率为100%是一致的.
观察表9.2-1和图9.2-1,你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
观察表9.2-1你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
数据分析
(1)从频率分布表中可以看出,样本观测数据落在各个小组的比例大小.
例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小,等等.
数据分析
观察图9.2-1你觉得这组数据蕴含了哪些有用的信息?你能从图表中发现居民用户月均用水量的哪些分布规律?你能给出适当的语言描述吗?
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
(2)从频率分布直方图能直观地表明数据分布的形状和总体趋势.可以看出,数据的分布不对称,图形左边高、右边低,右边有一个较长的“尾巴”。这表明大部分居民用户的月均用水量集中在一个较低值区域,尤其在[1.2,7.2)最为集中,少数用户居民的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
根据100户居民用户的月均用水量的频率分布,可以推测该市全体居民用户月均用水量也会有类似的分布,即大部分居民用户月均用水量集中在较低值区域.
规律总结
你能根据样本观测数据的频率分布,估计总体的取值规律吗?
我们利用样本观测数据对整体情况的估计一定准确吗?
这使我们确定用水量标准时,可以定一个合适的值,以达到既不影响大多数居民用户的水费支出,又能节水的目的.
由于样本的随机性,这种估计可能会存在一定误差,但这一误差一般不会影响我们对总体分布情况的大致了解.
除了样本的随机性,还有哪些因素会影响人们对整体的判断呢?
组数为3
组数为5
组数为9
组数为13
组数为16
组数为24
组数为27
探究 分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分布直方图(9.2-2).观察图形,你发现不同的组数对于直方图呈现数据分布规律有什么影响?
组数少、组距大:易看出数据整体的分布特点,无法看出每组内的数据分布情况,损失了较多的原始数据信息;
组数多、组距小:保留较多原始数据信息;但小长方形较多,有时图形会变得不规则,不容易从中看出总体分布特点;
直方图会依赖样本数据,稳定性差.
1. 从某小区抽取100户居民用户进行月用电量调查,发现他们的用电量都在50~350 kW h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示.
(1) 直方图中x的值为________;
(2) 在被调查的用户中,用电量落在区间[100,250) 内的户数为_____.
70
0.0044
课堂练习
(1)由频率分布直方图中各小长方形的总面积为1,
得(0.002 4+0.003 6+0.006 0+0.002 4+0.001 2+x)×50=1,
得x=0.004 4.
(2)用电量在[100,250)内的频率为
(0.003 6+0.006 0+0.004 4)×50=0.7,
因此用电量在区间[100,250)内的户数为0.7×100=70.
解:(1) 通话时长在区间[15,20),[20,30)内的次数分别为9次和12次.
(2) 区间[20,30)内的通话次数 少于区间[15,20内的通话次数.
2.如图,胡晓统计了他爸爸9月的手机通话明细清单,发现他爸爸该月共通话60次. 胡晓按每次通话时间长短进行分组(每组为左闭右开的区间),画出了频率分布直方图.
(1) 通话时长在区间[15,20),[20,30) 内的次数分别为多少
(2) 区间[20, 30)上的小长方形高度低于[15, 20)上的小长方形的高度,说明什么
课堂练习
课堂小结
通过本节课的学习你收获了哪些知识?掌握了哪些方法?体会了哪些思想呢?
课堂小结
本节课我们了解了统计学解决问题的基本思路,研究了列频率分布表、画频率分布直方图的方法,并利用图表整理数据,分析样本数据取值规律,并借助样本数据取值规律对总体数据取值规律进行估计.提升数学运算、数据分析素养,不同分组方法也会影响对总体的判断,因此要注意积累数据分组、合理使用图表的经验.
布置作业
2.课本199第3题.
谢谢聆听!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
