平面向量的概念及运算[上学期]
图片预览








文档简介
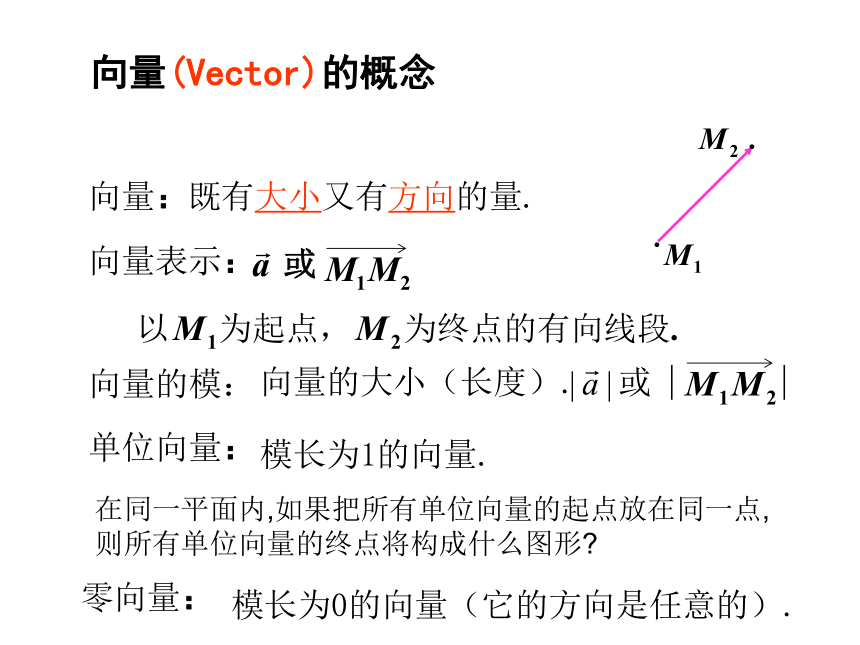
课件29张PPT。平面向量的概念及运算向量:既有大小又有方向的量.向量表示:模长为1的向量.零向量:模长为0的向量(它的方向是任意的).向量的模:向量的大小(长度).单位向量: 向量(Vector)的概念或或在同一平面内,如果把所有单位向量的起点放在同一点,则所有单位向量的终点将构成什么图形?相等向量:大小相等且方向相同的向量.相反向量:大小相等但方向相反的向量.∥一、概念巩固: 1、下列各量中是向量的是( )
(A)面积 (B)时间 (C)质量 (D)速度D 2、下列说法中正确的是( )
(A)平行向量就是向量所在直线都平行
的向量
(B)长度相等的向量叫做相等向量
(C)零向量的长度为0
(D)共线向量就是在同一直线上的向量C 3、下列说法中错误的是( )
(A)零向量是没有方向的
(B)零向量的长度为0
(C)零向量与任一向量平行
(D)零向量的方向是任意的A4、判断正误(1)零向量的方向是任意的.(2)若 ,则(3)若 ,则(√)(√)(√)(4)单位向量都平行.(×)(5)单位向量都相等.(×)(6)单位向量的模都相等.(√)(8)若 ,则(×)(9)若 ,则(√)(√)(10)零向量与任何向量都平行.(11)平行向量一定是共线向量.(×)(√)(√)1 加法(Addition):(平行四边形法则)特殊地:若‖分为同向和反向 向量的线性运算(Operations of Vectors)2、三角形法则向量加法的基本性质: 对于任意向量α、β、γ,有 (1) α+β=β+α(交换律);
(2) (α+β)+γ=α+(β+γ)(结合律);(3) α+0=0+α=α; (4) α+(-α)=0.三个向量α,β,γ的和可以简记为α+β+γ, n个向量α1,α2,…,αn的和可以简记为α1+α2+…+αn 。 s=α1+α2+α3+α4+α5例如2 减法(Subtraction)(Multiplication by Numbers)3 向量与数的乘法数与向量的乘积符合下列运算律(1)结合律:(2)分配律:(3)分配律:向量相加及数乘向量统称为向量的线性运算..平面向量的基本定理 若 是平面上两个不共线向量,则此平面上的
任意一个向量 均可表示为下列形式:证 充分性.如果β=mα,由数乘向量的定义知,β与α共线,充分性得证.必要性.由于β与α共线,且|α|≠0,因而有非负实数λ使得 λ. 当β与α同向时,可取m=λ;?
定理 设向量α≠O,向量β与α共线的充分必要条件是,存在唯一的实数m,使β=mα.当β与α反向时,可取m=-λ,最后证明β=mα中的m是唯一的. 若β=m1,α=m2,则(m1-m2)α=0 ,因为α≠0,所以 m1=m2 .? 推论 向量α1、α2共线的充分必要条件是存在不全为零的实数k1,k2,使得k1α1+k2α2=0.
于是都有β=mα1、O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足 = +λ( + )
λ∈[0,+∞)
则P的轨迹一定通过△ABC的( )
A.外心 B.内心 C.重心 D.垂心向量的夹角平面向量的数量积的定义规定:零向量与任意向量的数量积为0,即 0. (1)两向量的数量积是一个数量,而不是向量,符号由夹角决定 (3) a · b不能写成a×b ,a×b 表示向量的另一种运算.(2)一种新的运算法则,以前所学的运算律、性质不适合.3、投影的定义 叫做向量 在 方向上的投影 OC= 4、向量的数量积的几何意义:
向量 的模乘以 向量在 方向上的投影,等于
与 的数量积
讨论总结性质:(1)e · a=a · e=| a | cos? (2)a⊥b a · b=0 (判断两向量垂直的依据) (3)当a 与b 同向时,a · b =| a | · | b |,当a 与b 反向
时, a · b =—| a | · | b | .
特别地(4)(5)a · b ≤| a | · | b |例题选讲: 例⒈已知 ,当
① ∥ ;② ⊥ ;③ 与 夹角为600时,
分别求 与 的数量积。
故选B例3、已知a、b都是非零向量,且a + 3 b 与7 a – 5 b 垂直,a – 4 b 与7 a – 2 b垂直,求a与b的夹角。 解:∵ (a + 3 b )⊥(7 a – 5 b)
(a – 4 b )⊥(7 a – 2 b )
∴ (a + 3 b )·(7 a – 5 b) =0 且
(a – 4 b )· (7 a – 2 b )=0
即 7a ·a + 16 a ·b – 15 b · b =0
7a ·a - 30 a · b + 8 b ·b =0
两式相减得: 2 a ·b = b 2,
代入其中任一式中得: a 2= b 2
(A)面积 (B)时间 (C)质量 (D)速度D 2、下列说法中正确的是( )
(A)平行向量就是向量所在直线都平行
的向量
(B)长度相等的向量叫做相等向量
(C)零向量的长度为0
(D)共线向量就是在同一直线上的向量C 3、下列说法中错误的是( )
(A)零向量是没有方向的
(B)零向量的长度为0
(C)零向量与任一向量平行
(D)零向量的方向是任意的A4、判断正误(1)零向量的方向是任意的.(2)若 ,则(3)若 ,则(√)(√)(√)(4)单位向量都平行.(×)(5)单位向量都相等.(×)(6)单位向量的模都相等.(√)(8)若 ,则(×)(9)若 ,则(√)(√)(10)零向量与任何向量都平行.(11)平行向量一定是共线向量.(×)(√)(√)1 加法(Addition):(平行四边形法则)特殊地:若‖分为同向和反向 向量的线性运算(Operations of Vectors)2、三角形法则向量加法的基本性质: 对于任意向量α、β、γ,有 (1) α+β=β+α(交换律);
(2) (α+β)+γ=α+(β+γ)(结合律);(3) α+0=0+α=α; (4) α+(-α)=0.三个向量α,β,γ的和可以简记为α+β+γ, n个向量α1,α2,…,αn的和可以简记为α1+α2+…+αn 。 s=α1+α2+α3+α4+α5例如2 减法(Subtraction)(Multiplication by Numbers)3 向量与数的乘法数与向量的乘积符合下列运算律(1)结合律:(2)分配律:(3)分配律:向量相加及数乘向量统称为向量的线性运算..平面向量的基本定理 若 是平面上两个不共线向量,则此平面上的
任意一个向量 均可表示为下列形式:证 充分性.如果β=mα,由数乘向量的定义知,β与α共线,充分性得证.必要性.由于β与α共线,且|α|≠0,因而有非负实数λ使得 λ. 当β与α同向时,可取m=λ;?
定理 设向量α≠O,向量β与α共线的充分必要条件是,存在唯一的实数m,使β=mα.当β与α反向时,可取m=-λ,最后证明β=mα中的m是唯一的. 若β=m1,α=m2,则(m1-m2)α=0 ,因为α≠0,所以 m1=m2 .? 推论 向量α1、α2共线的充分必要条件是存在不全为零的实数k1,k2,使得k1α1+k2α2=0.
于是都有β=mα1、O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足 = +λ( + )
λ∈[0,+∞)
则P的轨迹一定通过△ABC的( )
A.外心 B.内心 C.重心 D.垂心向量的夹角平面向量的数量积的定义规定:零向量与任意向量的数量积为0,即 0. (1)两向量的数量积是一个数量,而不是向量,符号由夹角决定 (3) a · b不能写成a×b ,a×b 表示向量的另一种运算.(2)一种新的运算法则,以前所学的运算律、性质不适合.3、投影的定义 叫做向量 在 方向上的投影 OC= 4、向量的数量积的几何意义:
向量 的模乘以 向量在 方向上的投影,等于
与 的数量积
讨论总结性质:(1)e · a=a · e=| a | cos? (2)a⊥b a · b=0 (判断两向量垂直的依据) (3)当a 与b 同向时,a · b =| a | · | b |,当a 与b 反向
时, a · b =—| a | · | b | .
特别地(4)(5)a · b ≤| a | · | b |例题选讲: 例⒈已知 ,当
① ∥ ;② ⊥ ;③ 与 夹角为600时,
分别求 与 的数量积。
故选B例3、已知a、b都是非零向量,且a + 3 b 与7 a – 5 b 垂直,a – 4 b 与7 a – 2 b垂直,求a与b的夹角。 解:∵ (a + 3 b )⊥(7 a – 5 b)
(a – 4 b )⊥(7 a – 2 b )
∴ (a + 3 b )·(7 a – 5 b) =0 且
(a – 4 b )· (7 a – 2 b )=0
即 7a ·a + 16 a ·b – 15 b · b =0
7a ·a - 30 a · b + 8 b ·b =0
两式相减得: 2 a ·b = b 2,
代入其中任一式中得: a 2= b 2
