22.3实践与探索(第2课时)面积问题课件(共20张PPT)2022-2023学年华东师大版九年级数学上册
文档属性
| 名称 | 22.3实践与探索(第2课时)面积问题课件(共20张PPT)2022-2023学年华东师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 364.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 09:06:54 | ||
图片预览







文档简介
(共20张PPT)
第2课时 面积问题
九年级上
1. 会建立与面积相关的一元二次方程数学模型.
2. 能运用一元二次方程解决与面积相关的实际问题.
学习目标
重点
难点
直接开平方法、配方法、公式法、因式分解法.
问题1 解一元二次方程有哪些方法?
问题2 列一元一次方程解应用题的步骤:
①审题;②找等量关系;③列方程;④解方程;⑤答.
那么列一元二次方程解应用题的步骤呢?你知道吗?
新课引入
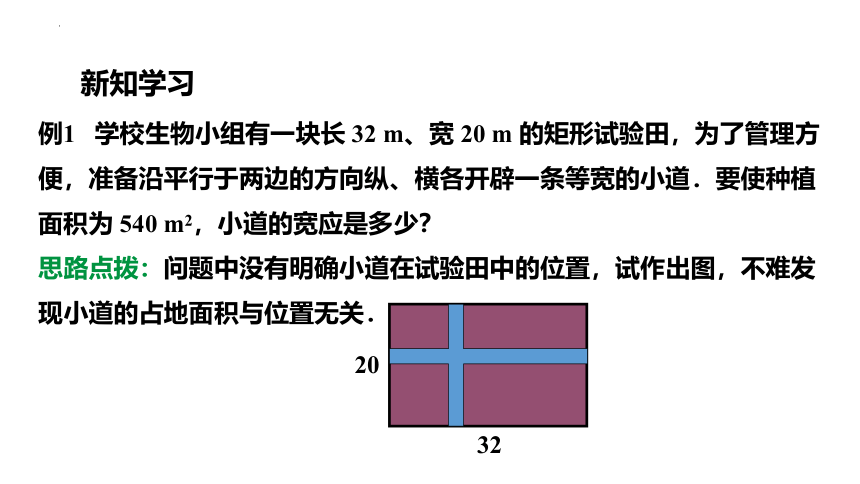
例1 学校生物小组有一块长 32 m、宽 20 m 的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道.要使种植面积为 540 m2,小道的宽应是多少?
思路点拨:问题中没有明确小道在试验田中的位置,试作出图,不难发现小道的占地面积与位置无关.
20
32
新知学习
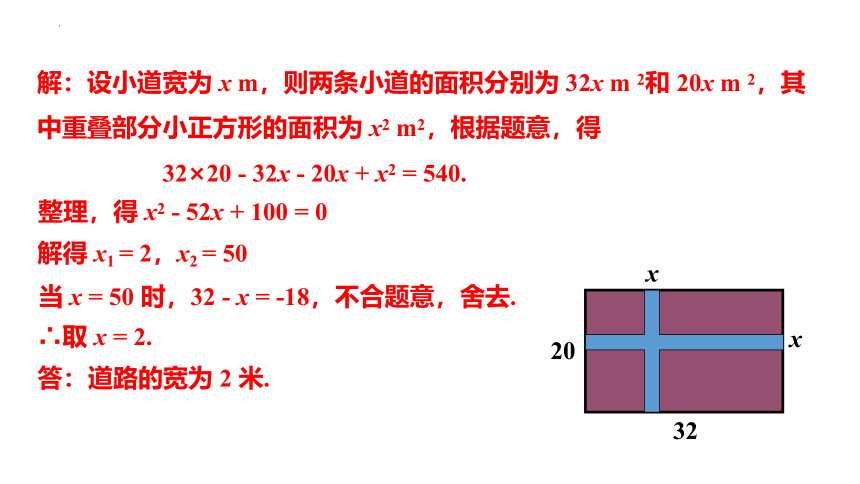
解:设小道宽为 x m,则两条小道的面积分别为 32x m 2和 20x m 2,其中重叠部分小正方形的面积为 x2 m2,根据题意,得
32×20 - 32x - 20x + x2 = 540.
整理,得 x2 - 52x + 100 = 0
解得 x1 = 2,x2 = 50
∴取 x = 2.
答:道路的宽为 2 米.
当 x = 50 时,32 - x = -18,不合题意,舍去.
20
32
x
x
如果设想把小道平移到两边,如图所示,小道所占面积是否保持不变?在这样的设想下,所列方程是否符合题目要求?处理问题是否方便些?
试一试
20
32
x
x
20-x
32-x
在应用一元二次方程解决实际问题时,与应用一元一次方程一样,要注意分析题意,抓住等量关系,列出方程,把实际问题转化为数学问题来解决.求得方程的根之后,要注意检验是否符合题意,最后得到实际问题的解答.
归纳
例2 如图,要设计一本书的封面,封面长 27cm,宽 21cm,正中央是一个与整个封面长宽比例相同的矩形. 如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?( 精确到 0.1cm )
27cm
21cm
思路点拨:封面的长宽之比是 27:21=9:7,中央的矩形的长宽之比也应是9:7. 设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是
=9(3-a):7(3-a)
=9:7.
27cm
21cm
解:设上下边衬的宽为 9x cm,左右边衬的宽为 7x cm,依题意得
∴上、下边衬的宽均为 1.8 cm
左、右边衬的宽均为 1.4 cm
27cm
21cm
思考
如果换一种设未知数的方法,是否可以更简单地解决上面的问题 请你试一试.
27cm
21cm
解: 设正中央的矩形两边长分别为 9x cm,7x cm.
依题意得
解得
故上下边衬的宽度为:
左右边衬的宽度为:
27cm
21cm
针对训练
1. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为 864 平方步,只知道它的长与宽共 60 步,问它的长比宽多多少步?请解答上述问题.
解:设长为 x 步,则宽为 (60-x) 步,由题意,得 x(60-x) = 864,
解得 x1 = 36,x2 = 24(舍去),
∴x = 36,60-x=24,
∴长比宽多36-24=12步.答:长比宽多12步.
2. 要为一幅长29 cm,宽22 cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米?(结果保留小数点后一位)
解:设镜框边的宽度为 x cm,则
有(29+2x)(22+2x)=( +1)×(29×22),即 4x2+102x-159.5 = 0,
解得x1=1.48,x2= -26.98(舍去).
答:镜框边的宽度应是1.48cm.
1. 在宽为 28m,长为 30m 的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为 675m2,则这种方案下的道路的宽为多少?
随堂练习
整理,得 x2 – 58x +165 = 0
解得 x1=3,x2=55
当 x = 55 时,30 – x = -25,不合题意,舍去.
∴取 x = 3.
答:道路的宽为3米.
解:设道路的宽为 x 米.
(30 – x)(28 – x)=675
可列方程为
解:设此矩形的宽为 x cm,则长为 ( 20-x ) cm. 根据题意,得 x(20-x)=75.
解得:x1 = 5,x2 = 15( 舍去 ).
故能围成一个面积为 75 cm2的矩形,该矩形的宽为5 cm,长为15 cm;
由 x(20-x)=101,即 x2-20x+101=0,
知 Δ = 202-4×101 = -4<0,方程无解,
故不能围成一个面积为101 cm2的矩形.
2. 用一条长40 cm的绳子怎样围成一个面积为 75cm2 的矩形?能围成一个面积为 101cm2 的矩形吗?如能,说明围法;如不能,说明理由.
你会解这
道题吗?
3.如图,把一张边长为10 cm 的正方形硬纸片的四周各剪去一个相同的小正方形,然后折叠成底面积为 81 cm2 的没有盖的长方体盒子.求截去的小正方形的边长.
10
10
10 - 2x
10 - 2x
x
x
解:设剪去的小正方形的边长 x cm,则长方体盒子的长和宽都为 (10 - 2x) cm.依题意得
(10 - 2x)2=81
得 x1=9.5,x2=0.5.
检验:
当 x1=9.5 时,
长、宽都为 10-2x=-9 cm(不符合题意 舍去)
当 x2=0.5时,
长,宽都为 10-2x=9cm(符合题意)
答:截取的小正方形的边长是 15 cm.
10
10
10 - 2x
10 - 2x
x
x
1. 用一元二次方程解决图形问题时,通常要先画出图形,利用图形的面积找相等关系列方程. 修路问题,通常采用平移方法,使剩余部分为一完整矩形.
2. 列一元二次方程解决实际问题时要注意对答案进行检验,看是否符合题的实际意义.
课堂小结
第2课时 面积问题
九年级上
1. 会建立与面积相关的一元二次方程数学模型.
2. 能运用一元二次方程解决与面积相关的实际问题.
学习目标
重点
难点
直接开平方法、配方法、公式法、因式分解法.
问题1 解一元二次方程有哪些方法?
问题2 列一元一次方程解应用题的步骤:
①审题;②找等量关系;③列方程;④解方程;⑤答.
那么列一元二次方程解应用题的步骤呢?你知道吗?
新课引入
例1 学校生物小组有一块长 32 m、宽 20 m 的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横各开辟一条等宽的小道.要使种植面积为 540 m2,小道的宽应是多少?
思路点拨:问题中没有明确小道在试验田中的位置,试作出图,不难发现小道的占地面积与位置无关.
20
32
新知学习
解:设小道宽为 x m,则两条小道的面积分别为 32x m 2和 20x m 2,其中重叠部分小正方形的面积为 x2 m2,根据题意,得
32×20 - 32x - 20x + x2 = 540.
整理,得 x2 - 52x + 100 = 0
解得 x1 = 2,x2 = 50
∴取 x = 2.
答:道路的宽为 2 米.
当 x = 50 时,32 - x = -18,不合题意,舍去.
20
32
x
x
如果设想把小道平移到两边,如图所示,小道所占面积是否保持不变?在这样的设想下,所列方程是否符合题目要求?处理问题是否方便些?
试一试
20
32
x
x
20-x
32-x
在应用一元二次方程解决实际问题时,与应用一元一次方程一样,要注意分析题意,抓住等量关系,列出方程,把实际问题转化为数学问题来解决.求得方程的根之后,要注意检验是否符合题意,最后得到实际问题的解答.
归纳
例2 如图,要设计一本书的封面,封面长 27cm,宽 21cm,正中央是一个与整个封面长宽比例相同的矩形. 如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?( 精确到 0.1cm )
27cm
21cm
思路点拨:封面的长宽之比是 27:21=9:7,中央的矩形的长宽之比也应是9:7. 设中央的矩形的长和宽分别是 9a cm和 7a cm,由此得上、下边衬与左、右边衬的宽度之比是
=9(3-a):7(3-a)
=9:7.
27cm
21cm
解:设上下边衬的宽为 9x cm,左右边衬的宽为 7x cm,依题意得
∴上、下边衬的宽均为 1.8 cm
左、右边衬的宽均为 1.4 cm
27cm
21cm
思考
如果换一种设未知数的方法,是否可以更简单地解决上面的问题 请你试一试.
27cm
21cm
解: 设正中央的矩形两边长分别为 9x cm,7x cm.
依题意得
解得
故上下边衬的宽度为:
左右边衬的宽度为:
27cm
21cm
针对训练
1. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为 864 平方步,只知道它的长与宽共 60 步,问它的长比宽多多少步?请解答上述问题.
解:设长为 x 步,则宽为 (60-x) 步,由题意,得 x(60-x) = 864,
解得 x1 = 36,x2 = 24(舍去),
∴x = 36,60-x=24,
∴长比宽多36-24=12步.答:长比宽多12步.
2. 要为一幅长29 cm,宽22 cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米?(结果保留小数点后一位)
解:设镜框边的宽度为 x cm,则
有(29+2x)(22+2x)=( +1)×(29×22),即 4x2+102x-159.5 = 0,
解得x1=1.48,x2= -26.98(舍去).
答:镜框边的宽度应是1.48cm.
1. 在宽为 28m,长为 30m 的矩形地面上修筑同样宽的道路,余下的部分种上草坪,要使草坪的面积为 675m2,则这种方案下的道路的宽为多少?
随堂练习
整理,得 x2 – 58x +165 = 0
解得 x1=3,x2=55
当 x = 55 时,30 – x = -25,不合题意,舍去.
∴取 x = 3.
答:道路的宽为3米.
解:设道路的宽为 x 米.
(30 – x)(28 – x)=675
可列方程为
解:设此矩形的宽为 x cm,则长为 ( 20-x ) cm. 根据题意,得 x(20-x)=75.
解得:x1 = 5,x2 = 15( 舍去 ).
故能围成一个面积为 75 cm2的矩形,该矩形的宽为5 cm,长为15 cm;
由 x(20-x)=101,即 x2-20x+101=0,
知 Δ = 202-4×101 = -4<0,方程无解,
故不能围成一个面积为101 cm2的矩形.
2. 用一条长40 cm的绳子怎样围成一个面积为 75cm2 的矩形?能围成一个面积为 101cm2 的矩形吗?如能,说明围法;如不能,说明理由.
你会解这
道题吗?
3.如图,把一张边长为10 cm 的正方形硬纸片的四周各剪去一个相同的小正方形,然后折叠成底面积为 81 cm2 的没有盖的长方体盒子.求截去的小正方形的边长.
10
10
10 - 2x
10 - 2x
x
x
解:设剪去的小正方形的边长 x cm,则长方体盒子的长和宽都为 (10 - 2x) cm.依题意得
(10 - 2x)2=81
得 x1=9.5,x2=0.5.
检验:
当 x1=9.5 时,
长、宽都为 10-2x=-9 cm(不符合题意 舍去)
当 x2=0.5时,
长,宽都为 10-2x=9cm(符合题意)
答:截取的小正方形的边长是 15 cm.
10
10
10 - 2x
10 - 2x
x
x
1. 用一元二次方程解决图形问题时,通常要先画出图形,利用图形的面积找相等关系列方程. 修路问题,通常采用平移方法,使剩余部分为一完整矩形.
2. 列一元二次方程解决实际问题时要注意对答案进行检验,看是否符合题的实际意义.
课堂小结
