北师大版数学六年级下册 总复习-图形与测量 第一课时 图形与测量课件(共33张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 总复习-图形与测量 第一课时 图形与测量课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 14:43:18 | ||
图片预览











文档简介
(共33张PPT)
总 复 习
图形与测量
第一课时 图形与测量
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
探索与发现
02
探索与发现
结合实例,说一说你对长度、面积、体积的认识。
探索与发现
1.长度的意义:长度指的是线段的长短。如:给草坪围上篱笆,要测量出篱笆的长度。
2.面积的意义:面积指物体所占的平面的大小。如:给地面铺上草坪,要测量并计算出草坪占多大的面积;给柱子刷漆,要测量并计算出所要刷漆的面积。
3.体积的意义:体积是指物体所占的空间的大小。如给水池注满水,要测量并计算出所需水的体积。
探索与发现
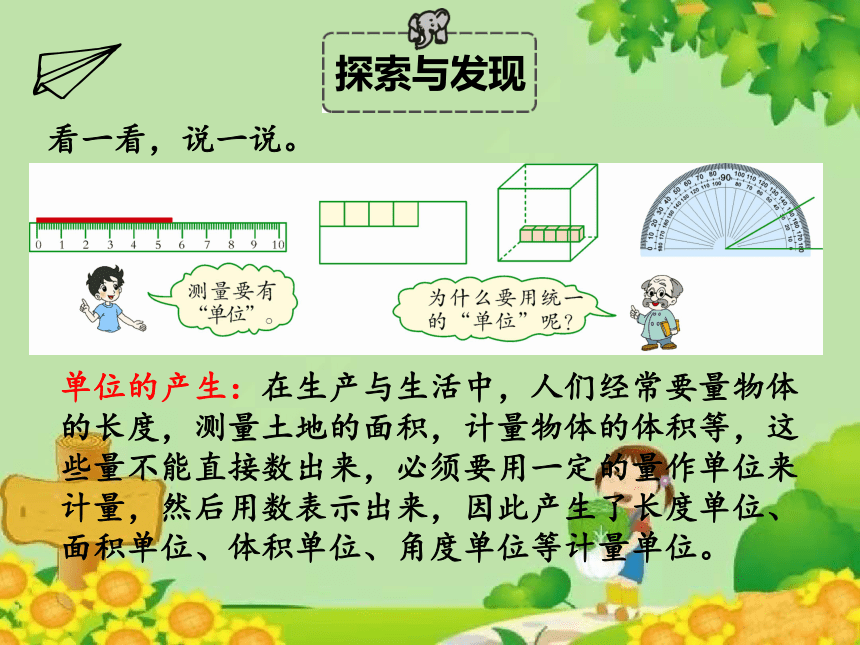
看一看,说一说。
单位的产生:在生产与生活中,人们经常要量物体的长度,测量土地的面积,计量物体的体积等,这些量不能直接数出来,必须要用一定的量作单位来计量,然后用数表示出来,因此产生了长度单位、面积单位、体积单位、角度单位等计量单位。
探索与发现
常见的计量单位:
长度单位: 毫米(mm) 厘米(cm) 分米(dm)
米(m) 千米(km)
面积单位:平方毫米(mm2) 平方厘米(cm2)
平方分米(dm2) 平方米(m2)
体积单位:立方毫米(mm3) 立方厘米(cm3)
立方分米(dm3) 立方米(m3)
容积单位:升(L) 毫升(mL)
角的单位:度(°)
探索与发现
填一填。
探索与发现
借助实例说一说1 m,1 dm,1 cm分别有多长;1 m2,1 dm2,1 cm2,1 m3,1 L,1 mL分别有多大。
1 m:如小学生两臂伸长的长度;米尺的长度。
1 dm:如水芯笔的长度;粉笔盒的棱长。
1 cm:如手指甲盖的宽;数学书的厚度。
1 m2:边长是1 m的正方形,面积是1 m2。如:教室里铺的大理石砖的面积;家用小方桌的面积。
探索与发现
1 dm2:边长是1 dm的正方形,面积是1 dm2。
如:墙壁上灯的开关盒面的面积;吃饭用的碗的碗口的面积。
1 cm2:边长是1 cm的正方形,面积是1 cm2。
如:衣服的纽扣的面积;指甲盖的面积。
1 m3:棱长是1 m的正方体,体积是1 m3。
如:一台滚筒洗衣机的体积;讲桌的体积。
1 L:1 L=1 dm3,棱长是1 dm的正方体,体积是 1 dm3,即1L。
如:粉笔盒的容积;一瓶可乐的容积。
1 mL:1 mL=1 cm3,棱长是1 cm的正方体,体积是1 cm3,即1mL。
如:骰子;咖啡方糖。
探索与发现
与同伴交流,你是如何量角的。在估计角的大小时,你有什么好的办法。
度量角的方法:
(1)中心对顶点(量角器的中心与角的顶点对齐重合);
(2)零线对一边(量角器0刻度线与一条起始边对齐重合);
(3)它边看度数(角的另一条边所对的是角的度数);
(4)内外要分辨(量角器上有两条0刻度线,一条是内圈的,一条是外圈的;0刻度线在内圈,度数就读内圈;
0刻度线在外圈,度数就读外圈)。
探索与发现
估计角的方法:
以直角为标准,先观察比直角大还是比直角小,如果比直角小,就看要估计的角大约占直角的几分之几,从而估出度数;如果比直角大,就看要估计的角大约比直角大几分之几,从而估出度数。
探索与发现
想办法求出下面图形的周长,并说说什么是周长。
周长的意义:围成图形一周的长度叫作这个图形的周长。
探索与发现
知识点一:平面图形的周长与面积的概念
1、周长的概念:
2、面积的概念:
围成一个图形的所有边长的总和叫作这个图形的周长。
物体的表面或围成的平面图形的大小,叫作它的面积。
探索与发现
知识点二:平面图形的周长与面积的计算公式。
探索与发现
想一想圆的面积计算公式的探索过程,并说一说圆的面积公式。
圆的面积计算公式:
已知半径:S=πr2;
已知直径:S=π(d2)2;
已知周长:S=π(C÷π÷2)2。
探索与发现
举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
立体图形的表面积计算方法:
长方体的表面积=(长×宽+长×高+宽×高)
×2S=2(ab+ah+bh)
正方体的表面积=棱长×棱长×6S=6a2
圆柱的侧面积=底面周长×高
S侧=Ch
圆柱的表面积=侧面积+两个底面的面积
S表=Ch+2πr2
探索与发现
分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
学以致用
03
学以致用
dm
m
cm
cm2
mL
cm3
40
7.5
41.6
7.25
0.062
2800
320
240000
320
500
8750
0.064
学以致用
1200
1200
400
400
300
600
学以致用
A=5cm2
B=6cm2
C=2cm2
D≈9cm2
学以致用
62.8÷3.14
×4=
80(cm)
答:正方形的周长是80cm。
学以致用
(60+80)×30÷2-
1500(dm2)
(1)
60×20÷2=
(2)
方法①
①
7×4+
61(dm2)
(15-4)×
(7-4)=
方法②
②
4×4+
61(dm2)
15×
(7-4)=
方法③
③
15×7-
61(dm2)
(15-4)×
4 =
学以致用
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃?
(2)哪个鱼缸盛水多?先猜一猜,再计算多了多少升?
长方体:
60×40+
60×50
×2+
40×50
×2=
12400(cm2)
正方体:
50×50
×5=
12500(cm2)
长方体:
60×40×50=
120000(mL)=
正方体:
50×50×50=
125000(mL)=
120(L)
125(L)
125-120=
5(L)
答:正方体鱼缸盛水多,多5L。
学以致用
3.14×6×
22608(cm2)=
12
×100=
226.08(dm2)
答:至少共需要226.08平方分米的广告纸。
学以致用
9.一圆锥形小麦堆的地面周长为15.7m,高1.5m。如果每立方米小麦的质量为700kg,这堆小麦的质量约为多少千克?
15.7÷3.14÷2=
2.5(m)
9.8125×700=
6868.75(kg)
答:这堆小麦的质量约为6868.75千克。
×3.14×2.52×1.5=
9.8125(m2)
3
1
学以致用
48÷4=
12(dm)
12-8= 4(dm)
2×8×4+
2×2=
68(dm2)
答:至少需要68平方分米的纸。
4× =2(dm)
1+1
1
学以致用
3
2
3
3
6
1
9
2
1
42
54
58
cm
cm
cm
cm2
课后作业
04
感 谢 观 看
总 复 习
图形与测量
第一课时 图形与测量
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
探索与发现
02
探索与发现
结合实例,说一说你对长度、面积、体积的认识。
探索与发现
1.长度的意义:长度指的是线段的长短。如:给草坪围上篱笆,要测量出篱笆的长度。
2.面积的意义:面积指物体所占的平面的大小。如:给地面铺上草坪,要测量并计算出草坪占多大的面积;给柱子刷漆,要测量并计算出所要刷漆的面积。
3.体积的意义:体积是指物体所占的空间的大小。如给水池注满水,要测量并计算出所需水的体积。
探索与发现
看一看,说一说。
单位的产生:在生产与生活中,人们经常要量物体的长度,测量土地的面积,计量物体的体积等,这些量不能直接数出来,必须要用一定的量作单位来计量,然后用数表示出来,因此产生了长度单位、面积单位、体积单位、角度单位等计量单位。
探索与发现
常见的计量单位:
长度单位: 毫米(mm) 厘米(cm) 分米(dm)
米(m) 千米(km)
面积单位:平方毫米(mm2) 平方厘米(cm2)
平方分米(dm2) 平方米(m2)
体积单位:立方毫米(mm3) 立方厘米(cm3)
立方分米(dm3) 立方米(m3)
容积单位:升(L) 毫升(mL)
角的单位:度(°)
探索与发现
填一填。
探索与发现
借助实例说一说1 m,1 dm,1 cm分别有多长;1 m2,1 dm2,1 cm2,1 m3,1 L,1 mL分别有多大。
1 m:如小学生两臂伸长的长度;米尺的长度。
1 dm:如水芯笔的长度;粉笔盒的棱长。
1 cm:如手指甲盖的宽;数学书的厚度。
1 m2:边长是1 m的正方形,面积是1 m2。如:教室里铺的大理石砖的面积;家用小方桌的面积。
探索与发现
1 dm2:边长是1 dm的正方形,面积是1 dm2。
如:墙壁上灯的开关盒面的面积;吃饭用的碗的碗口的面积。
1 cm2:边长是1 cm的正方形,面积是1 cm2。
如:衣服的纽扣的面积;指甲盖的面积。
1 m3:棱长是1 m的正方体,体积是1 m3。
如:一台滚筒洗衣机的体积;讲桌的体积。
1 L:1 L=1 dm3,棱长是1 dm的正方体,体积是 1 dm3,即1L。
如:粉笔盒的容积;一瓶可乐的容积。
1 mL:1 mL=1 cm3,棱长是1 cm的正方体,体积是1 cm3,即1mL。
如:骰子;咖啡方糖。
探索与发现
与同伴交流,你是如何量角的。在估计角的大小时,你有什么好的办法。
度量角的方法:
(1)中心对顶点(量角器的中心与角的顶点对齐重合);
(2)零线对一边(量角器0刻度线与一条起始边对齐重合);
(3)它边看度数(角的另一条边所对的是角的度数);
(4)内外要分辨(量角器上有两条0刻度线,一条是内圈的,一条是外圈的;0刻度线在内圈,度数就读内圈;
0刻度线在外圈,度数就读外圈)。
探索与发现
估计角的方法:
以直角为标准,先观察比直角大还是比直角小,如果比直角小,就看要估计的角大约占直角的几分之几,从而估出度数;如果比直角大,就看要估计的角大约比直角大几分之几,从而估出度数。
探索与发现
想办法求出下面图形的周长,并说说什么是周长。
周长的意义:围成图形一周的长度叫作这个图形的周长。
探索与发现
知识点一:平面图形的周长与面积的概念
1、周长的概念:
2、面积的概念:
围成一个图形的所有边长的总和叫作这个图形的周长。
物体的表面或围成的平面图形的大小,叫作它的面积。
探索与发现
知识点二:平面图形的周长与面积的计算公式。
探索与发现
想一想圆的面积计算公式的探索过程,并说一说圆的面积公式。
圆的面积计算公式:
已知半径:S=πr2;
已知直径:S=π(d2)2;
已知周长:S=π(C÷π÷2)2。
探索与发现
举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
立体图形的表面积计算方法:
长方体的表面积=(长×宽+长×高+宽×高)
×2S=2(ab+ah+bh)
正方体的表面积=棱长×棱长×6S=6a2
圆柱的侧面积=底面周长×高
S侧=Ch
圆柱的表面积=侧面积+两个底面的面积
S表=Ch+2πr2
探索与发现
分别说出已学过的立体图形的体积计算公式,并说说公式之间的联系。
学以致用
03
学以致用
dm
m
cm
cm2
mL
cm3
40
7.5
41.6
7.25
0.062
2800
320
240000
320
500
8750
0.064
学以致用
1200
1200
400
400
300
600
学以致用
A=5cm2
B=6cm2
C=2cm2
D≈9cm2
学以致用
62.8÷3.14
×4=
80(cm)
答:正方形的周长是80cm。
学以致用
(60+80)×30÷2-
1500(dm2)
(1)
60×20÷2=
(2)
方法①
①
7×4+
61(dm2)
(15-4)×
(7-4)=
方法②
②
4×4+
61(dm2)
15×
(7-4)=
方法③
③
15×7-
61(dm2)
(15-4)×
4 =
学以致用
(1)做上面两个无盖鱼缸,至少各需要多少平方厘米玻璃?
(2)哪个鱼缸盛水多?先猜一猜,再计算多了多少升?
长方体:
60×40+
60×50
×2+
40×50
×2=
12400(cm2)
正方体:
50×50
×5=
12500(cm2)
长方体:
60×40×50=
120000(mL)=
正方体:
50×50×50=
125000(mL)=
120(L)
125(L)
125-120=
5(L)
答:正方体鱼缸盛水多,多5L。
学以致用
3.14×6×
22608(cm2)=
12
×100=
226.08(dm2)
答:至少共需要226.08平方分米的广告纸。
学以致用
9.一圆锥形小麦堆的地面周长为15.7m,高1.5m。如果每立方米小麦的质量为700kg,这堆小麦的质量约为多少千克?
15.7÷3.14÷2=
2.5(m)
9.8125×700=
6868.75(kg)
答:这堆小麦的质量约为6868.75千克。
×3.14×2.52×1.5=
9.8125(m2)
3
1
学以致用
48÷4=
12(dm)
12-8= 4(dm)
2×8×4+
2×2=
68(dm2)
答:至少需要68平方分米的纸。
4× =2(dm)
1+1
1
学以致用
3
2
3
3
6
1
9
2
1
42
54
58
cm
cm
cm
cm2
课后作业
04
感 谢 观 看
