人教版数学九年级上册 21.3 实际问题与一元二次方程第3课时 用一元二次方程解决几何问题 课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册 21.3 实际问题与一元二次方程第3课时 用一元二次方程解决几何问题 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 301.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 09:33:56 | ||
图片预览





文档简介
(共19张PPT)
第3课时 用一元二次方程解决几何问题
21.3 实际问题与一元二次方程
用一元二次方程解决实际问题的步骤:
知识回顾
一审二设三列四解五验答
学习目标:
1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型,并能根据具体问题的实际意义,检验结果是否合理。
2.列一元二次方程解有关特殊图形问题的应用题。
重点和难点:
用方程刻画出数学模型准确解决实际问题,体会转化思想在数学中的应用。
学习目标及重难点
1.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块试验地,要使试验地的面积为570平方米,问:道路宽为多少米
解:设道路宽为x米,则
化简得,
其中的 x=35>20,应舍去.
答:道路的宽为1米.
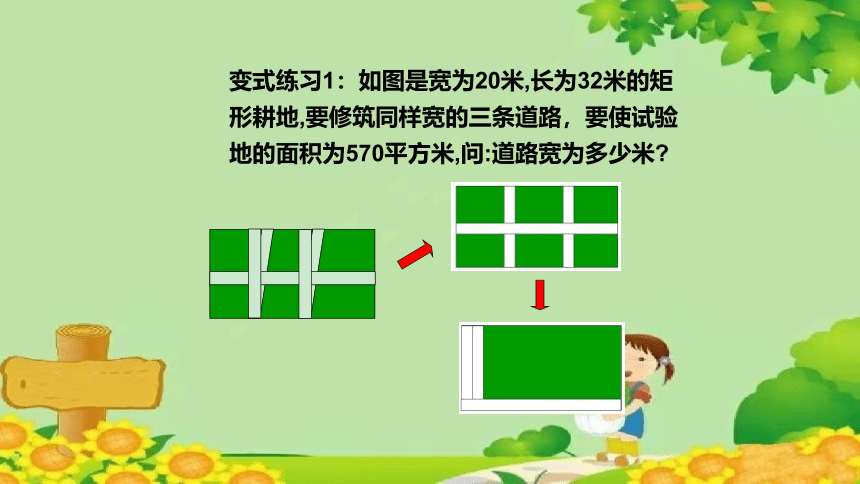
变式练习1:如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路,要使试验地的面积为570平方米,问:道路宽为多少米
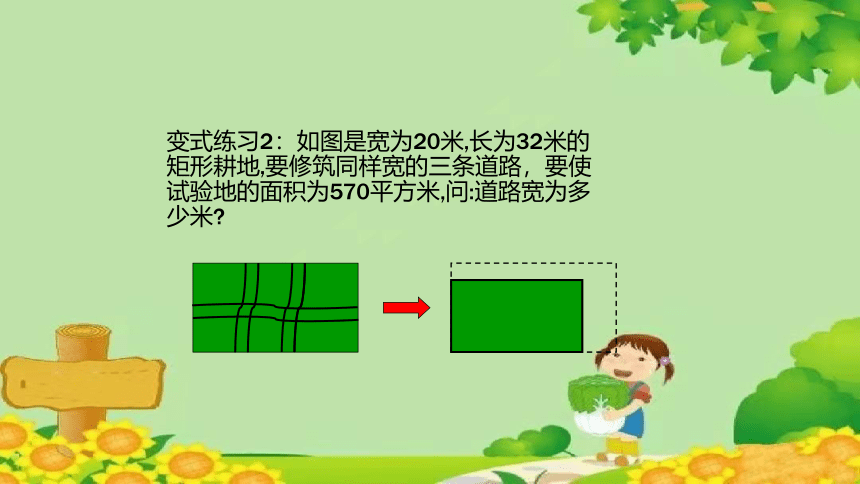
变式练习2:如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路,要使试验地的面积为570平方米,问:道路宽为多少米
探究3.要设计一本书的封面,封面长27㎝,宽21㎝,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度
解:设中央长为9x cm,宽均为7x cm.
由题意,可列出方程为:
9x 7x=
上下边衬宽为(27-9×2.6)/2=1.8(cm)
左右边衬宽为(27-7×2.6)/2=1.4(cm)
答:上下边衬宽为1.8cm,左右边衬宽为1.4cm。
解得x1≈2.6,x2≈-2.6(舍去).
分析:封面的长宽之比是27∶21=9∶7,中央的长方形的长宽之比也应是9∶7,若设中央的长方形的长和宽分别是9a cm和7a cm,由此得上下边衬与左右边衬的宽度之比是1/2(27-9a)∶1/2(21-7a)=
怎样设未知数可以更简单的解决上面的问题?
9:7
解:设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm.则中央矩形的长为(27-18x) cm,宽为(21-14x)cm
由题意,可列出方程为:
(27-18x)(21-14x)=
整理,得 16x2-48x+9=0
解方程,得
解得x1≈2.8,x2≈0.2
x为2.8时,中央矩形长和宽都为负数,舍去。
答:上下边衬宽为1.8cm,左右边衬宽为1.4cm。
3.如图,有长为24米的篱笆,一面利用(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S米2,
(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?
解:(1)设宽AB为x米,则BC为(24-3x)米,
S=x(24-3x)=-3x2+24x
(2)由条件-3x2+24x=45
化为:x2-8x+15=0解得x1=5,x2=3
∵0<24-3x≤10得14/3≤x<8
∴x2不合题意,AB=5,即花圃的宽AB为5米。
1.如图,某小区规划在一个长为40米、宽为26米的矩形场地上修建三条同样宽度的马路,其余部分种草.若使每一块草坪的面积都是144 m2,求马路的宽。
学以致用
解:设马路宽为x,根据题意得
(40-2x)(26-x)=144×6,
化简,得:x2-46x+88=0,
解得:x1=2,x2=44,
由题意:40-2x>0,26-x>0,则x<20.故x2=44不合题意,应舍去,∴x=2.
答:马路的宽为2 m.
2.要为一幅长29 cm,宽22 cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米?
解:设镜框边的宽度为x cm,则有(29+2x)(22+2x)=(1/4+1)×(29×22),即4x2+102x-159.5=0,
解得x1=1.48,x2=-26.98(舍去).
答:镜框边的宽度应是1.48cm.
3.用一根长40 cm的铁丝围成一个长方形,要求长方形的面积为75 cm2.
(1)求此长方形的宽是多少?
(2)能围成一个面积为101 cm2的长方形吗?如能,说明围法。
解:(1)设此长方形的宽为x cm,则长为(20-x)cm. 根据题意,得x(20-x)=75.
解得:x1=5,x2=15(舍去).
答:此长方形的宽是5 cm.
(2)不能.由x(20-x)=101,即x2-20x+101=0,
知Δ=202-4×101=-4<0,方程无解,故不能围成一个面积为101 cm2的长方形。
课堂小结
用一元二次方程解决的特殊图形问题时,通常要先画出图形,利用图形的面积找相等关系列方程。修路问题,通常采用平移方法,使剩余部分为一完整矩形。
列一元二次方程解决实际问题时要注意对答案进行检验,看是否符合题的实际意义。
第3课时 用一元二次方程解决几何问题
21.3 实际问题与一元二次方程
用一元二次方程解决实际问题的步骤:
知识回顾
一审二设三列四解五验答
学习目标:
1.能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型,并能根据具体问题的实际意义,检验结果是否合理。
2.列一元二次方程解有关特殊图形问题的应用题。
重点和难点:
用方程刻画出数学模型准确解决实际问题,体会转化思想在数学中的应用。
学习目标及重难点
1.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块试验地,要使试验地的面积为570平方米,问:道路宽为多少米
解:设道路宽为x米,则
化简得,
其中的 x=35>20,应舍去.
答:道路的宽为1米.
变式练习1:如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路,要使试验地的面积为570平方米,问:道路宽为多少米
变式练习2:如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路,要使试验地的面积为570平方米,问:道路宽为多少米
探究3.要设计一本书的封面,封面长27㎝,宽21㎝,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度
解:设中央长为9x cm,宽均为7x cm.
由题意,可列出方程为:
9x 7x=
上下边衬宽为(27-9×2.6)/2=1.8(cm)
左右边衬宽为(27-7×2.6)/2=1.4(cm)
答:上下边衬宽为1.8cm,左右边衬宽为1.4cm。
解得x1≈2.6,x2≈-2.6(舍去).
分析:封面的长宽之比是27∶21=9∶7,中央的长方形的长宽之比也应是9∶7,若设中央的长方形的长和宽分别是9a cm和7a cm,由此得上下边衬与左右边衬的宽度之比是1/2(27-9a)∶1/2(21-7a)=
怎样设未知数可以更简单的解决上面的问题?
9:7
解:设上、下边衬的宽均为9x cm,左、右边衬的宽均为7x cm.则中央矩形的长为(27-18x) cm,宽为(21-14x)cm
由题意,可列出方程为:
(27-18x)(21-14x)=
整理,得 16x2-48x+9=0
解方程,得
解得x1≈2.8,x2≈0.2
x为2.8时,中央矩形长和宽都为负数,舍去。
答:上下边衬宽为1.8cm,左右边衬宽为1.4cm。
3.如图,有长为24米的篱笆,一面利用(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S米2,
(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?
解:(1)设宽AB为x米,则BC为(24-3x)米,
S=x(24-3x)=-3x2+24x
(2)由条件-3x2+24x=45
化为:x2-8x+15=0解得x1=5,x2=3
∵0<24-3x≤10得14/3≤x<8
∴x2不合题意,AB=5,即花圃的宽AB为5米。
1.如图,某小区规划在一个长为40米、宽为26米的矩形场地上修建三条同样宽度的马路,其余部分种草.若使每一块草坪的面积都是144 m2,求马路的宽。
学以致用
解:设马路宽为x,根据题意得
(40-2x)(26-x)=144×6,
化简,得:x2-46x+88=0,
解得:x1=2,x2=44,
由题意:40-2x>0,26-x>0,则x<20.故x2=44不合题意,应舍去,∴x=2.
答:马路的宽为2 m.
2.要为一幅长29 cm,宽22 cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的四分之一,镜框边的宽度应是多少厘米?
解:设镜框边的宽度为x cm,则有(29+2x)(22+2x)=(1/4+1)×(29×22),即4x2+102x-159.5=0,
解得x1=1.48,x2=-26.98(舍去).
答:镜框边的宽度应是1.48cm.
3.用一根长40 cm的铁丝围成一个长方形,要求长方形的面积为75 cm2.
(1)求此长方形的宽是多少?
(2)能围成一个面积为101 cm2的长方形吗?如能,说明围法。
解:(1)设此长方形的宽为x cm,则长为(20-x)cm. 根据题意,得x(20-x)=75.
解得:x1=5,x2=15(舍去).
答:此长方形的宽是5 cm.
(2)不能.由x(20-x)=101,即x2-20x+101=0,
知Δ=202-4×101=-4<0,方程无解,故不能围成一个面积为101 cm2的长方形。
课堂小结
用一元二次方程解决的特殊图形问题时,通常要先画出图形,利用图形的面积找相等关系列方程。修路问题,通常采用平移方法,使剩余部分为一完整矩形。
列一元二次方程解决实际问题时要注意对答案进行检验,看是否符合题的实际意义。
同课章节目录
