华师大版数学七年级下册 7.4实践与探索课件(共15张PPT)
文档属性
| 名称 | 华师大版数学七年级下册 7.4实践与探索课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 671.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
7.4 实践与探索
一
学习目标
1.通过自主探索、相互交流,尝试用二元一次方程组解决 与生活密切相关的问题.
2.掌握列二元一次方程组解决实际问题的方法.
3.进一步经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的一个有效模型.
二
重难点
重点:让学生在实践与探索中,运用二元一次方程组解决实际问题.
难点:寻找等量关系列方程组.
1.知识回顾
三
教学过程
(1)列二元一次方程解决实际问题的步骤是什么?
(2)什么是二元一次方程组?
“审”“设”“列”解”“答”
把两个二元一次方程合在一起,就组成了一个二元一次方程组.
2.探究新知
问题1 要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?请你设计一种分法.想一想,如果可以将一张白卡纸裁出一个侧面和一个底面,那么该如何分这些白卡纸,才能使做出的侧面和底面配套,又能充分利用白卡纸?
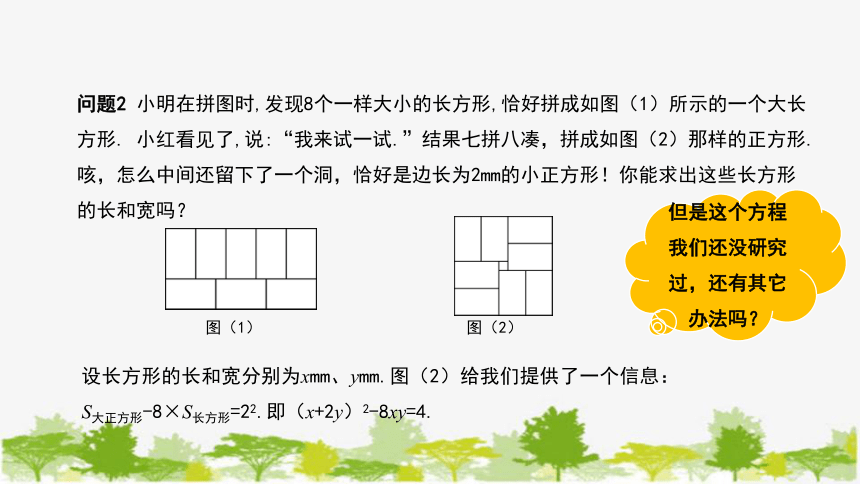
问题2 小明在拼图时,发现8个一样大小的长方形,恰好拼成如图(1)所示的一个大长方形. 小红看见了,说:“我来试一试.”结果七拼八凑,拼成如图(2)那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗?
设长方形的长和宽分别为xmm、ymm.图(2)给我们提供了一个信息:S大正方形-8×S长方形=22.即(x+2y)2-8xy=4.
但是这个方程我们还没研究过,还有其它办法吗?
图(1)
图(2)
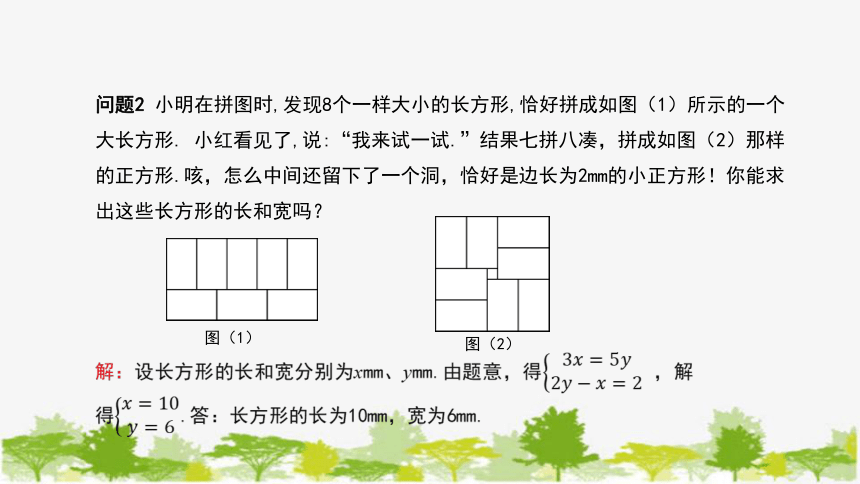
问题2 小明在拼图时,发现8个一样大小的长方形,恰好拼成如图(1)所示的一个大长方形. 小红看见了,说:“我来试一试.”结果七拼八凑,拼成如图(2)那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗?
图(1)
图(2)
【知识归纳】
列二元一次方程组解决实际问题的步骤:
(1)审:审题,找等量关系
(2)设:根据题意设未知数,包括直接设和间接设
(3)列:列二元一次方程组
(4)解:解方程组
(5)答:根据实际情况进行做答
例1 已知用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
【分析】(1)根据3辆A型车和2辆B型车载满货物一次可运货共19吨;2辆A型车和3辆B型车载满货物一次可运货共21吨,列出方程组即可解决问题.
3.例题精讲
(2)某物流公司现有49吨货物,计划同时租用A型车m辆,B型车n辆,一次运完,且恰好每辆车都载满货物.
①求m、n的值;
②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
【分析】 (2)①由题意得到3m+5n=49,根据m、n均为正整数,即可求出m、n的值.②求出每种方案下的租金数,经比较、分析,即可解决问题.
例2 某人乘汽车,他看到第一块里程碑上写着一个两位数(表示千米);经过1小时,他看到第二块里程碑写的两位数恰好和第一块里程碑上的数字互换了;又经过1小时,他看到第三块里程碑上写着一个三位数,这个三位数恰好为第一块里程碑上的两位数中间加上一个0,问汽车的速度是多少?
【分析】假设这个两位数的个位数字是x,十位数字是y,汽车的速度为z千米/小时,那么这个两位数数值就是10y+x,则1小时后站牌上的数值是10x+y,又经过1小时,他看到第三块里程碑上数值是100y+x,所以可列方程(10x+y)-(10y+x)=z与(100y+x)-(10x+y)=z,求得x与y的比例关系,再通过数字x、y满足0≤x≤9,1≤y≤9,确定出x、y的取值,代入即可求得z的值.
解:设这个两位数的个位数字是x,十位数字是y,汽车的速度为z千米/时.
由题意,得
化简,得 由③-④,得x=6y.
又∵0≤x≤9,1≤y≤9,且x、y为整数,
∴x只能取6,此时y=1,∴z=9×(6-1)=45.即汽车的速度是45千米/小时.
4.巩固练习 完成教材课后同步练习
5.课堂小结
列二元一次方程组解决实际问题的步骤:
(1)审:审题,找等量关系
(2)设:根据题意设未知数,包括直接设和间接设
(3)列:列二元一次方程组
(4)解:解方程组
(5)答:根据实际情况进行回答
7.4 实践与探索
一
学习目标
1.通过自主探索、相互交流,尝试用二元一次方程组解决 与生活密切相关的问题.
2.掌握列二元一次方程组解决实际问题的方法.
3.进一步经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的一个有效模型.
二
重难点
重点:让学生在实践与探索中,运用二元一次方程组解决实际问题.
难点:寻找等量关系列方程组.
1.知识回顾
三
教学过程
(1)列二元一次方程解决实际问题的步骤是什么?
(2)什么是二元一次方程组?
“审”“设”“列”解”“答”
把两个二元一次方程合在一起,就组成了一个二元一次方程组.
2.探究新知
问题1 要用20张白卡纸做长方体的包装盒,准备把这些白卡纸分成两部分,一部分做侧面,另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒,那么如何分才能使做成的侧面和底面正好配套?请你设计一种分法.想一想,如果可以将一张白卡纸裁出一个侧面和一个底面,那么该如何分这些白卡纸,才能使做出的侧面和底面配套,又能充分利用白卡纸?
问题2 小明在拼图时,发现8个一样大小的长方形,恰好拼成如图(1)所示的一个大长方形. 小红看见了,说:“我来试一试.”结果七拼八凑,拼成如图(2)那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗?
设长方形的长和宽分别为xmm、ymm.图(2)给我们提供了一个信息:S大正方形-8×S长方形=22.即(x+2y)2-8xy=4.
但是这个方程我们还没研究过,还有其它办法吗?
图(1)
图(2)
问题2 小明在拼图时,发现8个一样大小的长方形,恰好拼成如图(1)所示的一个大长方形. 小红看见了,说:“我来试一试.”结果七拼八凑,拼成如图(2)那样的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗?
图(1)
图(2)
【知识归纳】
列二元一次方程组解决实际问题的步骤:
(1)审:审题,找等量关系
(2)设:根据题意设未知数,包括直接设和间接设
(3)列:列二元一次方程组
(4)解:解方程组
(5)答:根据实际情况进行做答
例1 已知用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
【分析】(1)根据3辆A型车和2辆B型车载满货物一次可运货共19吨;2辆A型车和3辆B型车载满货物一次可运货共21吨,列出方程组即可解决问题.
3.例题精讲
(2)某物流公司现有49吨货物,计划同时租用A型车m辆,B型车n辆,一次运完,且恰好每辆车都载满货物.
①求m、n的值;
②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
【分析】 (2)①由题意得到3m+5n=49,根据m、n均为正整数,即可求出m、n的值.②求出每种方案下的租金数,经比较、分析,即可解决问题.
例2 某人乘汽车,他看到第一块里程碑上写着一个两位数(表示千米);经过1小时,他看到第二块里程碑写的两位数恰好和第一块里程碑上的数字互换了;又经过1小时,他看到第三块里程碑上写着一个三位数,这个三位数恰好为第一块里程碑上的两位数中间加上一个0,问汽车的速度是多少?
【分析】假设这个两位数的个位数字是x,十位数字是y,汽车的速度为z千米/小时,那么这个两位数数值就是10y+x,则1小时后站牌上的数值是10x+y,又经过1小时,他看到第三块里程碑上数值是100y+x,所以可列方程(10x+y)-(10y+x)=z与(100y+x)-(10x+y)=z,求得x与y的比例关系,再通过数字x、y满足0≤x≤9,1≤y≤9,确定出x、y的取值,代入即可求得z的值.
解:设这个两位数的个位数字是x,十位数字是y,汽车的速度为z千米/时.
由题意,得
化简,得 由③-④,得x=6y.
又∵0≤x≤9,1≤y≤9,且x、y为整数,
∴x只能取6,此时y=1,∴z=9×(6-1)=45.即汽车的速度是45千米/小时.
4.巩固练习 完成教材课后同步练习
5.课堂小结
列二元一次方程组解决实际问题的步骤:
(1)审:审题,找等量关系
(2)设:根据题意设未知数,包括直接设和间接设
(3)列:列二元一次方程组
(4)解:解方程组
(5)答:根据实际情况进行回答
