23.3.4相似三角形的应用课件(共18张PPT) 2022-2023学年华东师大版九年级数学上册
文档属性
| 名称 | 23.3.4相似三角形的应用课件(共18张PPT) 2022-2023学年华东师大版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 575.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 13:19:32 | ||
图片预览





文档简介
(共18张PPT)
23.3.4 相似三角形的应用
九年级上
1. 运用相似三角形的性质和判定解决实际问题;
2. 进一步了解数学建模思想,发展把实际问题抽象成数学问题的能力.
学习目标
重点
难点
泰勒斯应埃及法老的邀请来帮忙测量金字塔的高度,他把木棍插在金字塔旁边,等木棍的影子和木棍一样长的时候,他量了金字塔影子的长度和金字塔底面边长的一半,把这两个长度加起来就是金字塔的高度了.
你能解释泰勒斯用的什么原理么?
新课引入
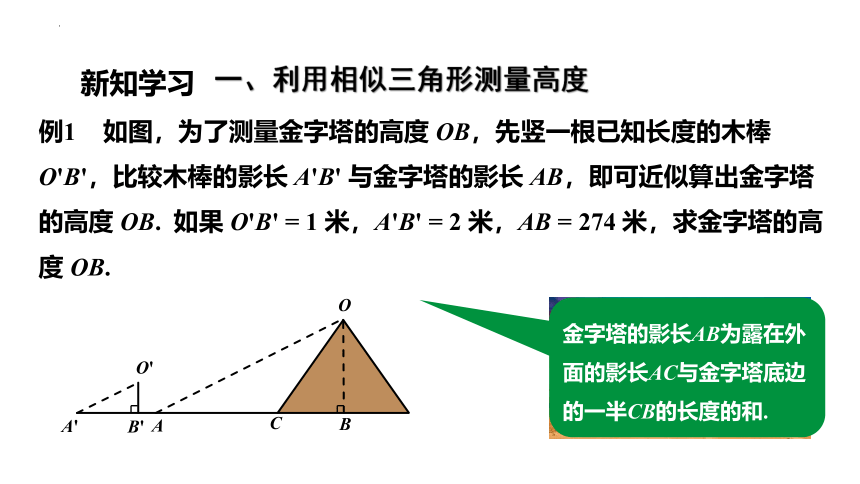
例1 如图,为了测量金字塔的高度 OB,先竖一根已知长度的木棒 O'B',比较木棒的影长 A'B' 与金字塔的影长 AB,即可近似算出金字塔的高度 OB. 如果 O'B' = 1 米,A'B' = 2 米,AB = 274 米,求金字塔的高度 OB.
A'
B'
O'
A
C
B
O
一、利用相似三角形测量高度
新知学习
金字塔的影长AB为露在外面的影长AC与金字塔底边的一半CB的长度的和.
解:∵太阳光线是平行光线,
∴∠OAB =∠O'A'B'.
∵∠ABO =∠A'B'O' = 90°,
∴△OAB∽△O'A'B' ( 两角分别相等的两个三角形相似 )
∴ = ,
∴OB = = = 137 ( 米 ),
答:金字塔的高度 OB 为 137 米.
A'
B'
O'
A
C
B
O
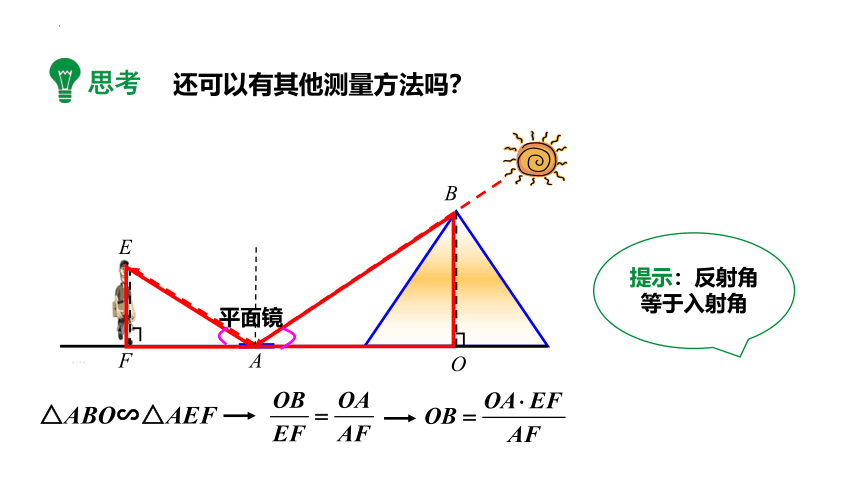
思考
还可以有其他测量方法吗?
A
F
E
B
O
┐
┐
△ABO∽△AEF
平面镜
提示:反射角等于入射角
测高方法二:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
针对训练
1. 在某一时刻,测得一根高为 1.8m 的竹竿的影长为 3m,同时测得一栋楼的影长为 90m,这栋楼的高度是多少?
解:设这栋楼的高度是 x m.
由题意得
解得 x = 54.
因此这栋楼的高度是 54m.
例2 如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点 A,再在河的这一边选定点 B 和 C,使 AB⊥BC,然后,再选定点 E,使 EC⊥BC,用视线确定 BC 和 AE 的交点 D. 此时如果测得 BD = 118 米,DC = 61 米,EC = 50 米,求河的宽度 AB. ( 精确到 0.1 米 )
A
B
D
C
E
二、利用相似三角形测量宽度
解:∵∠ADB =∠EDC,
∠ABD =∠ECD = 90°,
∴△ABD∽△ECD ( 两角分别相等的两个三角形相似 ),
∴ = ,
解得
AB = = ≈ 96.7 ( 米 )
答:河的宽度 AB 约为 96.7 米.
A
B
D
C
E
例3 如图,已知 D、E 分别是 △ABC 的边 AB、AC 上的点,且∠ADE = ∠C. 求证:AD·AB = AE·AC.
A
C
B
D
E
利用相似三角形,可以证明几条线段之间的乘积关系.
证明:∠ADE =∠C,∠A =∠A,
∴△ADE∽△ACB ( 两角分别相等的两个三角形相似 ),
∴ = ,
∴AD·AB = AE·AC.
A
C
B
D
E
针对训练
1. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔 5 米有一棵树,在北岸边每隔 50 米有一根电线杆.小丽站在离南岸边 15 米的点看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
22.5
1.为测量河两岸两根电线杆A,B间的距离,如图所示,有四位同学分别测量出了以下四组数据:(1)AC,DE,EF;(2)CD,DE,EF;(3)EF,DE,AD;(4)DE,DF,AD.其中,能根据所测数据求出A,B间距离的共有( )
A.1组 B.2组
C.3组 D.4组
B
随堂练习
A. 4 cm B. 5 cm
C. 6 cm D. 8 cm
2. 如图,有一点光源 S 在平面镜上方,若点 P 恰好在点光源 S 的反射光线上,并测得 AB = 10 cm,BC = 20 cm,PC⊥AC,且 PC = 12 cm,则点光源 S 到平面镜的距离 SA 的长度为 ( )
C
3. 如图,为了测量一栋楼的高度,王青同学在她脚底下放了一面镜子,然后向后退,直到她刚好在镜子中看到楼的顶部.这时 ∠LMK 等于∠SMT 吗?如果王青身高 1.55 m,她估计自己眼睛离地面 1.50 m,同时量得 LM = 0.30 m,MS = 2 m,这栋大楼有多高?
K
解:根据题意,
∵∠KLM =∠TSM = 90°,∠KML =∠TMS ( 反射角等于入射角 ),
∴△KLM ∽△TSM,
∴ 即
∴TS = 10 ( m )
所以这栋大楼高为 10 m.
K
1. 相似三角形的应用主要有哪两个方面?
(1) 测高 ( 不能直接使用皮尺或刻度尺测量 )
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测宽 ( 不能直接测量的两点间的距离 )
测量不能到达的两点间的距离,常构造相似三角形求解.
课堂小结
23.3.4 相似三角形的应用
九年级上
1. 运用相似三角形的性质和判定解决实际问题;
2. 进一步了解数学建模思想,发展把实际问题抽象成数学问题的能力.
学习目标
重点
难点
泰勒斯应埃及法老的邀请来帮忙测量金字塔的高度,他把木棍插在金字塔旁边,等木棍的影子和木棍一样长的时候,他量了金字塔影子的长度和金字塔底面边长的一半,把这两个长度加起来就是金字塔的高度了.
你能解释泰勒斯用的什么原理么?
新课引入
例1 如图,为了测量金字塔的高度 OB,先竖一根已知长度的木棒 O'B',比较木棒的影长 A'B' 与金字塔的影长 AB,即可近似算出金字塔的高度 OB. 如果 O'B' = 1 米,A'B' = 2 米,AB = 274 米,求金字塔的高度 OB.
A'
B'
O'
A
C
B
O
一、利用相似三角形测量高度
新知学习
金字塔的影长AB为露在外面的影长AC与金字塔底边的一半CB的长度的和.
解:∵太阳光线是平行光线,
∴∠OAB =∠O'A'B'.
∵∠ABO =∠A'B'O' = 90°,
∴△OAB∽△O'A'B' ( 两角分别相等的两个三角形相似 )
∴ = ,
∴OB = = = 137 ( 米 ),
答:金字塔的高度 OB 为 137 米.
A'
B'
O'
A
C
B
O
思考
还可以有其他测量方法吗?
A
F
E
B
O
┐
┐
△ABO∽△AEF
平面镜
提示:反射角等于入射角
测高方法二:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
针对训练
1. 在某一时刻,测得一根高为 1.8m 的竹竿的影长为 3m,同时测得一栋楼的影长为 90m,这栋楼的高度是多少?
解:设这栋楼的高度是 x m.
由题意得
解得 x = 54.
因此这栋楼的高度是 54m.
例2 如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点 A,再在河的这一边选定点 B 和 C,使 AB⊥BC,然后,再选定点 E,使 EC⊥BC,用视线确定 BC 和 AE 的交点 D. 此时如果测得 BD = 118 米,DC = 61 米,EC = 50 米,求河的宽度 AB. ( 精确到 0.1 米 )
A
B
D
C
E
二、利用相似三角形测量宽度
解:∵∠ADB =∠EDC,
∠ABD =∠ECD = 90°,
∴△ABD∽△ECD ( 两角分别相等的两个三角形相似 ),
∴ = ,
解得
AB = = ≈ 96.7 ( 米 )
答:河的宽度 AB 约为 96.7 米.
A
B
D
C
E
例3 如图,已知 D、E 分别是 △ABC 的边 AB、AC 上的点,且∠ADE = ∠C. 求证:AD·AB = AE·AC.
A
C
B
D
E
利用相似三角形,可以证明几条线段之间的乘积关系.
证明:∠ADE =∠C,∠A =∠A,
∴△ADE∽△ACB ( 两角分别相等的两个三角形相似 ),
∴ = ,
∴AD·AB = AE·AC.
A
C
B
D
E
针对训练
1. 如图,一条河的两岸有一段是平行的,在河的南岸边每隔 5 米有一棵树,在北岸边每隔 50 米有一根电线杆.小丽站在离南岸边 15 米的点看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为 米.
22.5
1.为测量河两岸两根电线杆A,B间的距离,如图所示,有四位同学分别测量出了以下四组数据:(1)AC,DE,EF;(2)CD,DE,EF;(3)EF,DE,AD;(4)DE,DF,AD.其中,能根据所测数据求出A,B间距离的共有( )
A.1组 B.2组
C.3组 D.4组
B
随堂练习
A. 4 cm B. 5 cm
C. 6 cm D. 8 cm
2. 如图,有一点光源 S 在平面镜上方,若点 P 恰好在点光源 S 的反射光线上,并测得 AB = 10 cm,BC = 20 cm,PC⊥AC,且 PC = 12 cm,则点光源 S 到平面镜的距离 SA 的长度为 ( )
C
3. 如图,为了测量一栋楼的高度,王青同学在她脚底下放了一面镜子,然后向后退,直到她刚好在镜子中看到楼的顶部.这时 ∠LMK 等于∠SMT 吗?如果王青身高 1.55 m,她估计自己眼睛离地面 1.50 m,同时量得 LM = 0.30 m,MS = 2 m,这栋大楼有多高?
K
解:根据题意,
∵∠KLM =∠TSM = 90°,∠KML =∠TMS ( 反射角等于入射角 ),
∴△KLM ∽△TSM,
∴ 即
∴TS = 10 ( m )
所以这栋大楼高为 10 m.
K
1. 相似三角形的应用主要有哪两个方面?
(1) 测高 ( 不能直接使用皮尺或刻度尺测量 )
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
(2) 测宽 ( 不能直接测量的两点间的距离 )
测量不能到达的两点间的距离,常构造相似三角形求解.
课堂小结
