【中考数学几何模型】第六节:费马点最值模型120-128(含答案)
文档属性
| 名称 | 【中考数学几何模型】第六节:费马点最值模型120-128(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 10:03:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第六节:费马点最值模型
120.矩形中的费马点最值问题(初二)
如图,已知矩形,点为矩形内一点,点为边上任意一点,则的最小值为( )
A.
B.
C.
D.10
121.直角三角形中的费马点最值问题(初二)
如图,在中,.若点是内一点,则的最小值为______.
122.菱形中的费马点最值问题(初二)
两张宽为的纸条交叉重叠成四边形,如图所示.若,则对角线上的动点到三点距离之和的最小值是_________.
123.阅读理解型费马点最值问题
已知到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果是锐角(或直角)三角形,则其费马点是三角形内一点,且满足.(例如:等边三角形的费马点是其三条高的交点).
(1).若为的费马点,则__________.
(2).若为的费马点,则___________.
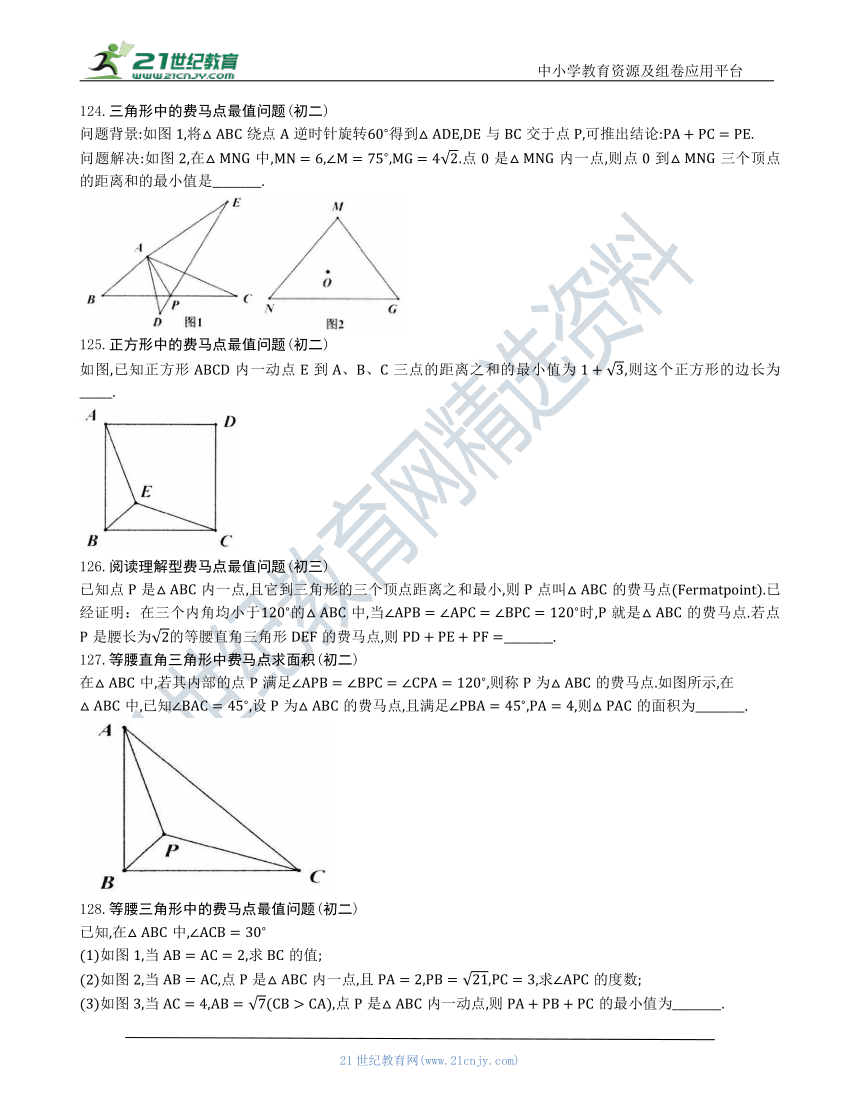
124.三角形中的费马点最值问题(初二)
问题背景:如图1,将绕点逆时针旋转得到与交于点,可推出结论:.
问题解决:如图2,在中,.点0是内一点,则点0到三个顶点的距离和的最小值是_________.
125.正方形中的费马点最值问题(初二)
如图,已知正方形内一动点到三点的距离之和的最小值为,则这个正方形的边长为______.
126.阅读理解型费马点最值问题(初三)
已知点是内一点,且它到三角形的三个顶点距离之和最小,则点叫的费马点(Fermatpoint).已经证明:在三个内角均小于的中,当时,就是的费马点.若点是腰长为的等腰直角三角形的费马点,则_________.
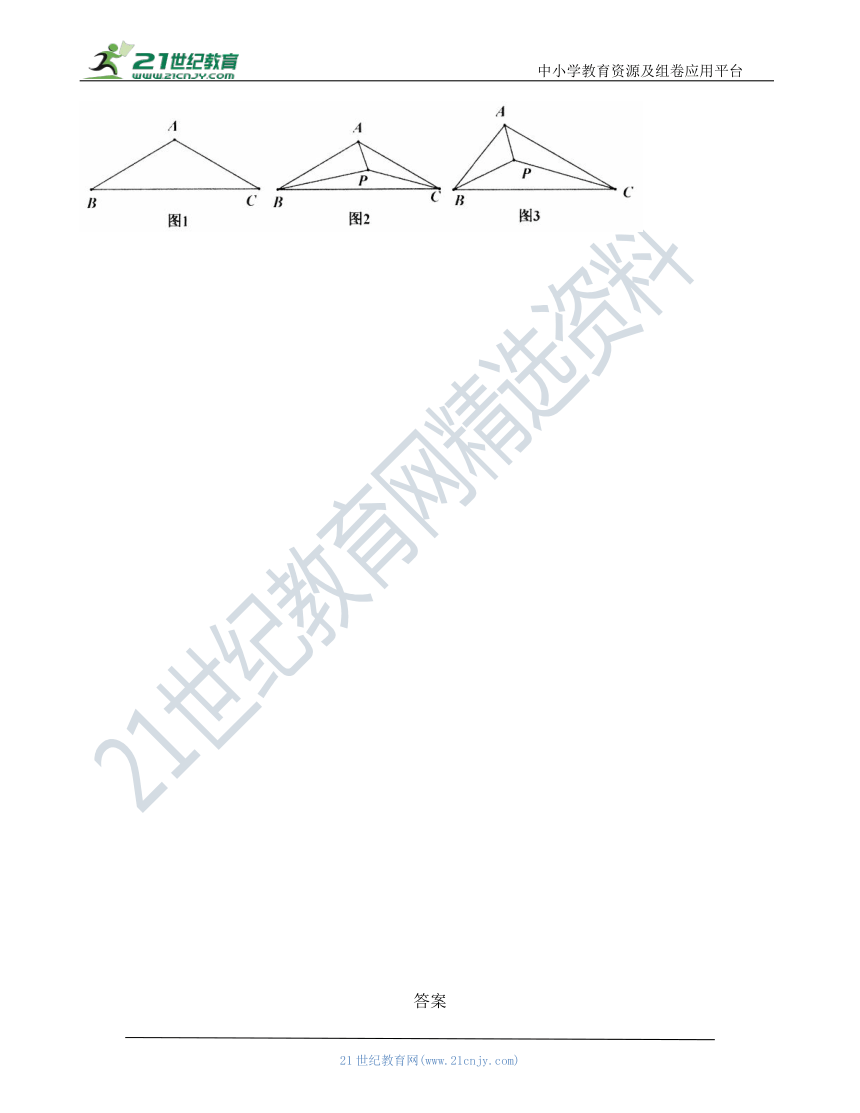
127.等腰直角三角形中费马点求面积(初二)
在中,若其内部的点满足,则称为的费马点.如图所示,在
中,已知,设为的费马点,且满足,则的面积为_________.
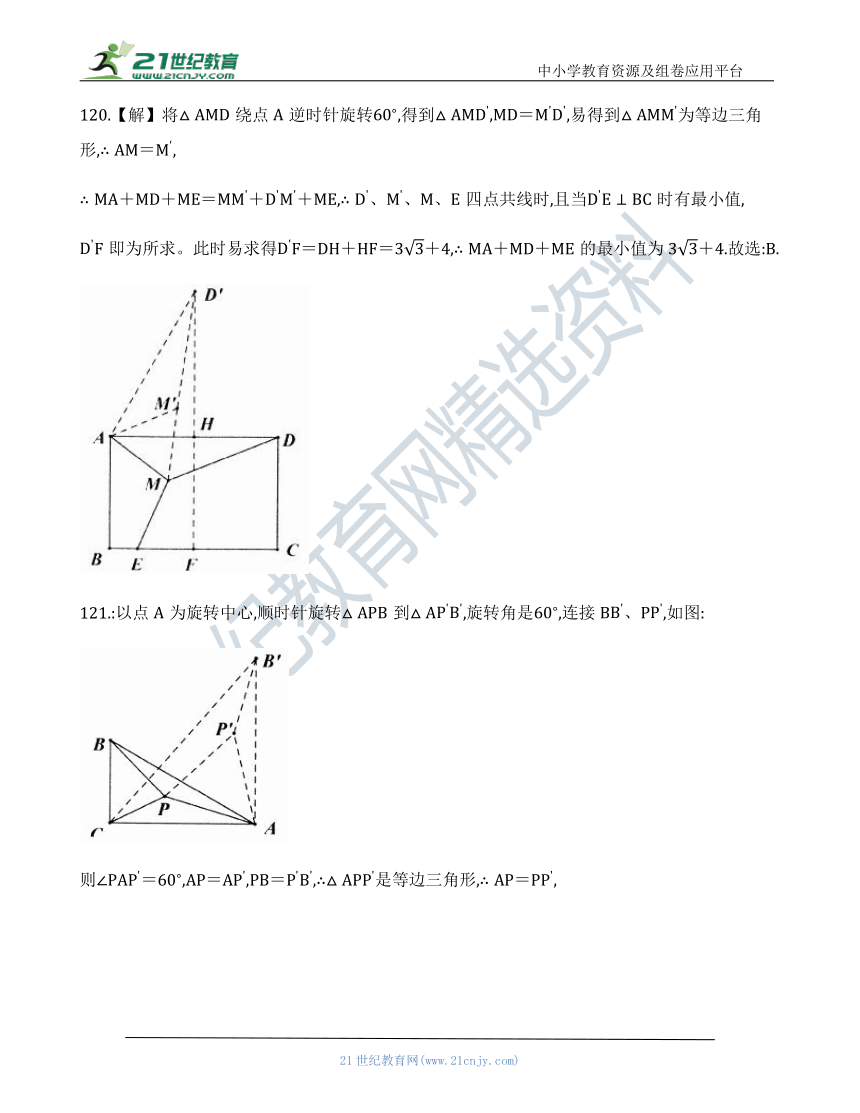
128.等腰三角形中的费马点最值问题(初二)
已知,在中,
(1)如图1,当,求的值;
(2)如图2,当,点是内一点,且,求的度数;
(3)如图3,当,点是内一动点,则的最小值为_________.
答案
120.【解】将绕点逆时针旋转,得到,易得到为等边三角形,,
,四点共线时,且当时有最小值,
F即为所求。此时易求得,的最小值为.故选:B.
121.:以点为旋转中心,顺时针旋转到,旋转角是,连接,如图:
则,是等边三角形,,
,的最小值就是的值,即的最小值就是的值,,,,故答案为:.
122.【解】如图,作于,把绕点逆时针旋转得到,
,同理:,由旋转的性质,
,是等边三角形,,
,
根据两点间线段距离最短,可知当时最短,连接,与的交点即为点,即点到,三点距离之和的最小值是.,
,因此点到三点距离之和的最小值是,故答案为.
123 .【解】(1).如图1,过作,垂足为,过分别作,则为的费马点,,,,
,;
(2).如图2:
∠,∴∠BAC=30°,将△APC绕点A,逆时针旋转60°,由旋转可得:
△APC≌△AP'C',∴AP'=AP,PC=P'C',AC=AC',∠CAC'=∠PAP'=60°,∴ΔAPP'是等边三角形,
∴∠BAC=90°,∵P为△ABC的费马点,即B,P,P',C四点共线时,PA+PB+PC=BC,
∴PA+PB+PC=BP+PP'+P'C=BC'==2,故答案为:5,2.
124.(1)如图,在EP上截取EP'=CP,易证△AEP'≌ΔΑCP(SAA),∴AP'=AP,∠EAP'=∠CAP,
∴∠PAP'=∠CAP+∠CAP'=∠EAP'+∠CAP'=60°,
∴△PAP'是等边三角形,∴PP'=PAPP'+P'E=PE,∴PA+PC=PE
(2)【解】如图:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形,∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME,在△GMO和△DME中:易证△GMO≌△DME(SAS),
∴OG=DE,∴NO+GO+MO=DE+OE+NO,
∴当D、E、O、N四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,
∴∠DMF=45°,MG=4,∴MF=DF=4,∴NF=MN+MF=6+4=10,
∴ND==2,∴MO+NO+GO最小值为2,故答案为2
125.【解】以为旋转中心,将顺时针旋转得到,连,过作交的延长线于点,如图,,为等边角形,,
,当取最小值时,折线成为线段,则
为等边三角形,,则,
在Rt中,设,,
,即正方形的边长为,故答案为:.
126.【解】如图:等腰Rt中,,.
过点作于点,则,过分别作,交DM于点,此时的点就是满足题意的费马点.,
故,则.故答案为:.
127.【解】如图,延长交于,
为的费马点,,,
,Rt中,,
,
Rt中,
的面积为.故答案为:.
128.【解】(1)如图1中,作于.,在Rt中,
,.
(2)如图2中,将绕点逆时针旋转得到.,
,,
.
(3).如图3中,将绕点逆时针旋转得到,连接,则.
当四点共线时,的值最小,的长即为所求的最小值,由,可得.
故答案为.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第六节:费马点最值模型
120.矩形中的费马点最值问题(初二)
如图,已知矩形,点为矩形内一点,点为边上任意一点,则的最小值为( )
A.
B.
C.
D.10
121.直角三角形中的费马点最值问题(初二)
如图,在中,.若点是内一点,则的最小值为______.
122.菱形中的费马点最值问题(初二)
两张宽为的纸条交叉重叠成四边形,如图所示.若,则对角线上的动点到三点距离之和的最小值是_________.
123.阅读理解型费马点最值问题
已知到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果是锐角(或直角)三角形,则其费马点是三角形内一点,且满足.(例如:等边三角形的费马点是其三条高的交点).
(1).若为的费马点,则__________.
(2).若为的费马点,则___________.
124.三角形中的费马点最值问题(初二)
问题背景:如图1,将绕点逆时针旋转得到与交于点,可推出结论:.
问题解决:如图2,在中,.点0是内一点,则点0到三个顶点的距离和的最小值是_________.
125.正方形中的费马点最值问题(初二)
如图,已知正方形内一动点到三点的距离之和的最小值为,则这个正方形的边长为______.
126.阅读理解型费马点最值问题(初三)
已知点是内一点,且它到三角形的三个顶点距离之和最小,则点叫的费马点(Fermatpoint).已经证明:在三个内角均小于的中,当时,就是的费马点.若点是腰长为的等腰直角三角形的费马点,则_________.
127.等腰直角三角形中费马点求面积(初二)
在中,若其内部的点满足,则称为的费马点.如图所示,在
中,已知,设为的费马点,且满足,则的面积为_________.
128.等腰三角形中的费马点最值问题(初二)
已知,在中,
(1)如图1,当,求的值;
(2)如图2,当,点是内一点,且,求的度数;
(3)如图3,当,点是内一动点,则的最小值为_________.
答案
120.【解】将绕点逆时针旋转,得到,易得到为等边三角形,,
,四点共线时,且当时有最小值,
F即为所求。此时易求得,的最小值为.故选:B.
121.:以点为旋转中心,顺时针旋转到,旋转角是,连接,如图:
则,是等边三角形,,
,的最小值就是的值,即的最小值就是的值,,,,故答案为:.
122.【解】如图,作于,把绕点逆时针旋转得到,
,同理:,由旋转的性质,
,是等边三角形,,
,
根据两点间线段距离最短,可知当时最短,连接,与的交点即为点,即点到,三点距离之和的最小值是.,
,因此点到三点距离之和的最小值是,故答案为.
123 .【解】(1).如图1,过作,垂足为,过分别作,则为的费马点,,,,
,;
(2).如图2:
∠,∴∠BAC=30°,将△APC绕点A,逆时针旋转60°,由旋转可得:
△APC≌△AP'C',∴AP'=AP,PC=P'C',AC=AC',∠CAC'=∠PAP'=60°,∴ΔAPP'是等边三角形,
∴∠BAC=90°,∵P为△ABC的费马点,即B,P,P',C四点共线时,PA+PB+PC=BC,
∴PA+PB+PC=BP+PP'+P'C=BC'==2,故答案为:5,2.
124.(1)如图,在EP上截取EP'=CP,易证△AEP'≌ΔΑCP(SAA),∴AP'=AP,∠EAP'=∠CAP,
∴∠PAP'=∠CAP+∠CAP'=∠EAP'+∠CAP'=60°,
∴△PAP'是等边三角形,∴PP'=PAPP'+P'E=PE,∴PA+PC=PE
(2)【解】如图:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形,∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME,在△GMO和△DME中:易证△GMO≌△DME(SAS),
∴OG=DE,∴NO+GO+MO=DE+OE+NO,
∴当D、E、O、N四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,
∴∠DMF=45°,MG=4,∴MF=DF=4,∴NF=MN+MF=6+4=10,
∴ND==2,∴MO+NO+GO最小值为2,故答案为2
125.【解】以为旋转中心,将顺时针旋转得到,连,过作交的延长线于点,如图,,为等边角形,,
,当取最小值时,折线成为线段,则
为等边三角形,,则,
在Rt中,设,,
,即正方形的边长为,故答案为:.
126.【解】如图:等腰Rt中,,.
过点作于点,则,过分别作,交DM于点,此时的点就是满足题意的费马点.,
故,则.故答案为:.
127.【解】如图,延长交于,
为的费马点,,,
,Rt中,,
,
Rt中,
的面积为.故答案为:.
128.【解】(1)如图1中,作于.,在Rt中,
,.
(2)如图2中,将绕点逆时针旋转得到.,
,,
.
(3).如图3中,将绕点逆时针旋转得到,连接,则.
当四点共线时,的值最小,的长即为所求的最小值,由,可得.
故答案为.
21世纪教育网(www.21cnjy.com)
同课章节目录
