【中考数学几何模型】第六节:费马点最值模型129-135(含答案)
文档属性
| 名称 | 【中考数学几何模型】第六节:费马点最值模型129-135(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 439.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第六节:费马点最值模型
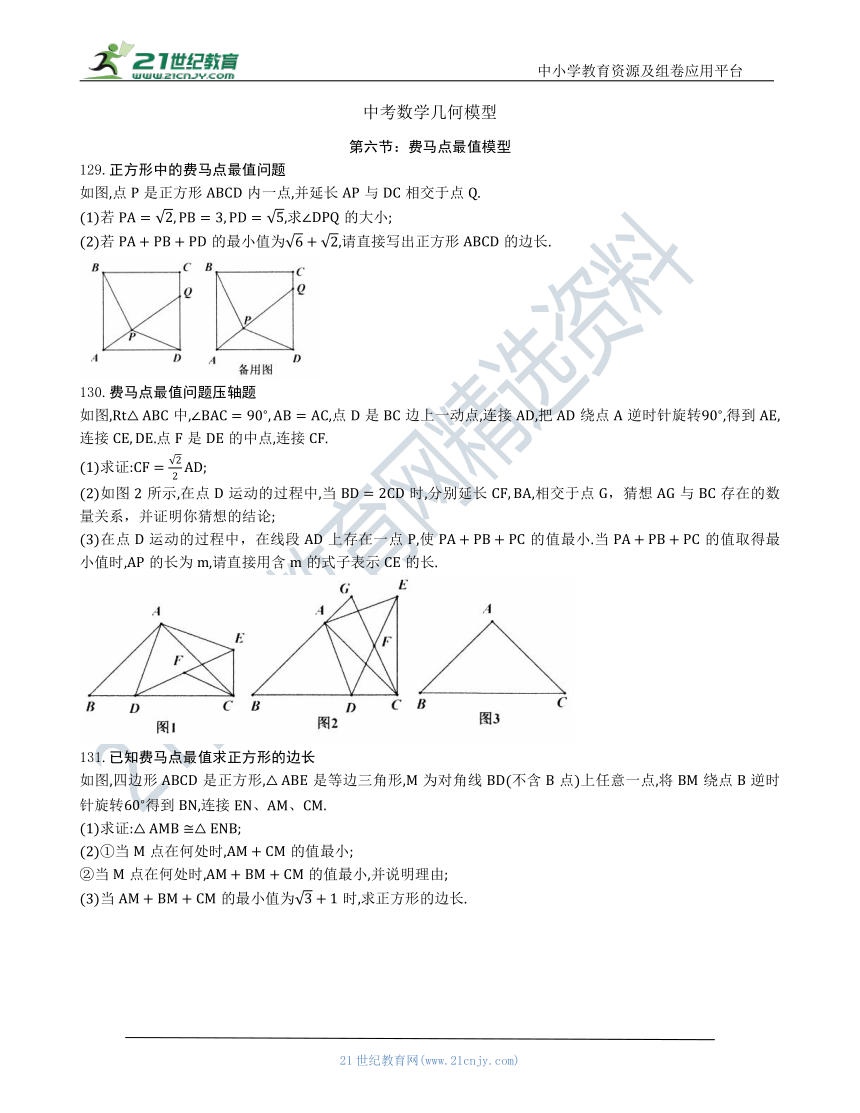
129.正方形中的费马点最值问题
如图,点是正方形内一点,并延长与相交于点.
(1)若,求的大小;
(2)若的最小值为,请直接写出正方形的边长.
130.费马点最值问题压轴题
如图,Rt中,,点是边上一动点,连接,把绕点逆时针旋转,得到,连接.点是的中点,连接.
(1)求证:;
(2)如图2所示,在点运动的过程中,当时,分别延长,相交于点,猜想与存在的数量关系,并证明你猜想的结论;
(3)在点运动的过程中,在线段上存在一点,使的值最小.当的值取得最小值时,的长为,请直接用含的式子表示的长.
131.已知费马点最值求正方形的边长
如图,四边形是正方形,是等边三角形,为对角线(不含点)上任意一点,将绕点逆时针旋转得到,连接.
(1)求证:;
(2)①当点在何处时,的值最小;
②当点在何处时,的值最小,并说明理由;
(3)当的最小值为时,求正方形的边长.
132.图形操作探究和拓展应用费马点最值问题
(1)【操作发现】如图1,将绕点顺时针旋转,得到,连接,则_________度.
(2)【类比探究】如图2,在等边三角形内任取一点,连接,求证:以的长为三边必能组成三角形.
(3)【解决问题】如图3,在边长为的等边三角形内有一点,求的面积.
(4)【拓展应用】如图4是A,B,C三个村子位置的平面图,经测量,为内的一个动点,连接.求的最小值.
133.从特例探究到拓展费马点最值问题
小颖在学习“两点之间线段最短”查阅资料时发现:内总存在一点与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点为等边的中心,将绕点逆时针旋转得到,从而有,连接得到,同时,,即四点共线,故.在中,另取一点,易知点与三个顶点连线的夹角不相等,可证明、四点不共线,所以,即点到三个顶点距离之和最小.
【探究】(1)如图2,为内一点,,证明的值最小;
【拓展】(2)如图3,中,,且点为内一点,求点到三个顶点的距离之和的最小值.
134.费马点最值模型的生产实践应用题
【问题情境】如图1,在中,,则的外接圆的半径值为_________.
【问题解决】如图2,点为正方形内一点,且,若,求AP的最小值.
【问题解决】如图3,正方形是一个边长为的隔离区域设计图,为大门,点在边上,,点是正方形内设立的一个活动岗哨,到的张角为,即,点为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点,使得到三个岗哨的距离和最小,试求的最小值.(保留根号或结果精确到,参考数据).
135.费马点模型的问题探究与应用
问题探究:将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.
问题提出:如图1,是边长为1的等边三角形,为内部一点,连接,求的最小值.
方法分析:通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).
问题解决:如图2,将绕点逆时针旋转至,连接PP',记与交于点,易知.由,可知为正三角形,有.
故.因此,当共线时,有最小值是.
学以致用:
(1)如图3,在中,为内部一点,连接,则的最小值是_________.
(2)如图4,在中,为内部一点,连接,求的最小值.
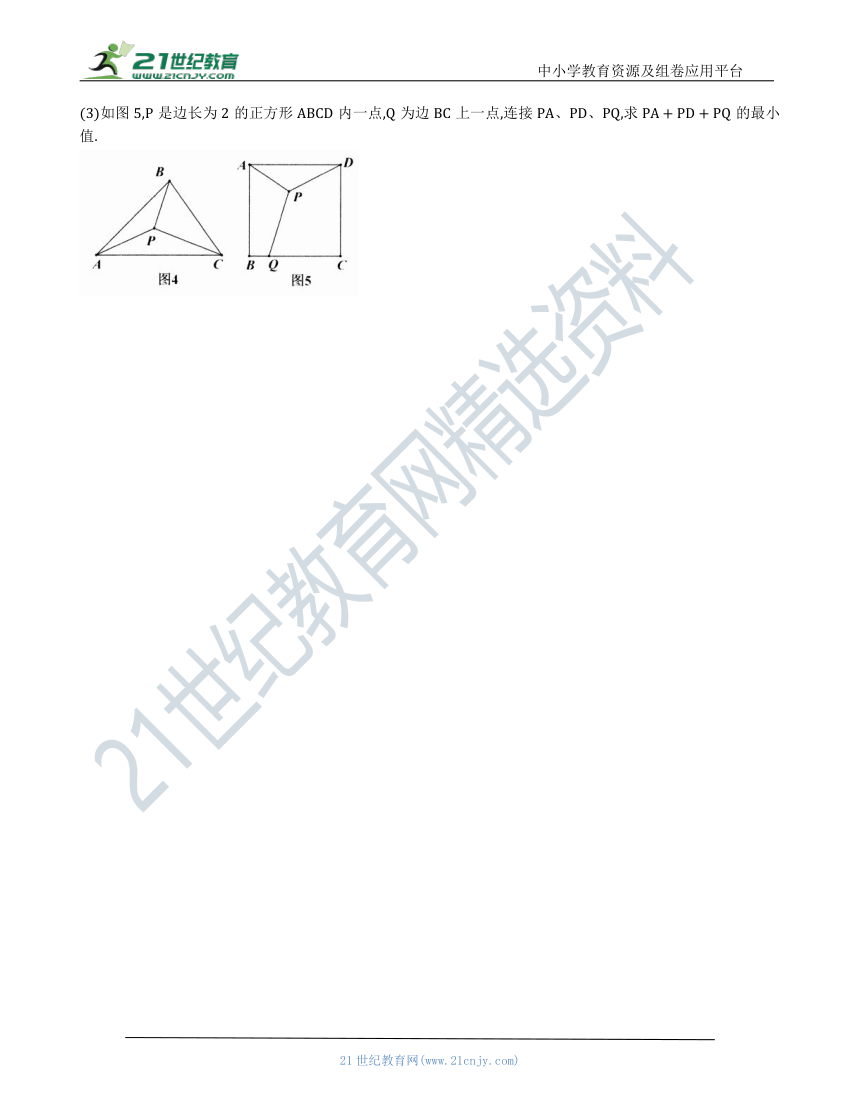
(3)如图5,是边长为2的正方形内一点,为边上一点,连接、,求的最小值.
答案
129.解(1)如图1,将绕点逆时针旋转得
,,
,
,,
.
(2).如图2,将绕点顺时针旋转得,连接,作交的延长线于.
当四点共线时,最小,这个最小值就是线段的长.,
是等边三角形,,设正方形边长为,Rt中,,,
在Rt中,,,
正方形边长为2.
130.证明:(1),
,把绕点逆时针旋转,得到,
,又,,
点是的中点,;
(2),理由如下:如下图,连接,由(1)可知,,又,
四点共圆,连接
四点共圆,
是等腰直角三角形,又
,又,
(3).如下图,将绕点顺时针旋转得到,连接,
是等边三角形,,
当四点共线时,值最小,此时,连接,即为的最小值.
连接,将绕点顺时针旋转得到,,
是等边三角形,是等边三角形,,
垂直平分,,
,
,由(1)可知:.
131.(1)证明:是等边二角形,.,
.即.又.
(2)【解】①当点落在的中点时,三点共线,的值最小.
②如图,连接,当点位于与的交点处时,的值最小,理由如下:连接,
由(1)知,,是等边三角形..
.根据“两点之间线段最短”可知,
若在同一条直线上时,取得最小值,最小值为.
在和中,易证(SAS),,
若连接,则,
可以同时在直线上.当点位于与的交点处时,的值最小,即等于的长.
(3)【解】过点作交的延长线于,.
设正方形的边长为,则.在Rt中,,
.解得(舍去负值).正方形的边长为.
132.(1)【操作发现】【解】如图,连接.
绕点顺时针旋转,得到,
是等边三角形,
故答案为60.
(2)【类比探究】证明:如图2中,以为边长作等边,使分别在的两侧,连接.
,
,
,在中,,
又的长为三边必能组成三角形.
(3)【解决问题】【解】如图3中,将绕点按逆时针方向旋转,得到是等边三角形,,,即,即,.(4)【拓展应用】【解】如图4中,将绕点顺时针旋转,得到,连接,则,.
将绕点顺时针旋转,得到,(旋转的性质),,是等边三角形,
当BPDE四点共线时,有最小值,BE即为所求.,
,,
在Rt中,,,
的最小值为;
133.【解】(1).如图2,将绕点逆时针旋转得到
为等边三角形,
,,
即四点共线,的值最小.
(2).【解】如图3,将绕点,顺时针旋转,得,易得即为所求的最小值。
在Rt中,
134.【解】(1)如图1,作的外接圆,作直径,连接是等边三角形,,设与交于点,在直角三角形中,,故答案为:5;
(2)如图2,点在以为直径的圆上,设圆心为点,则,
三点线时最小,在直角三角形中,,
的最小值为:;
(3)如图3,设所在圆的圆心为点,根据(1)可得所在圆的半径为,以点为旋转中心,将顺时针旋转,得到,当,共线时,最小,即为所求.过点作交的延长线于点,连接,则是等边三角形,过点作于交于点,连接,
四边形是正方形,,,
,是等边三形,
且,
,,
,最小值为:.
135.【解】(1)如图3,将绕点逆时针,旋转得到,易知是等边三角形,,
在Rt中,,
即为所求的最小值.的最小值为5.故答案为5.
(2)如图4中,将绕点逆时针旋转,得到,易知是等腰直角三角形,,作交的延长线于.在中,
,在Rt中,,,
即为所求的最小值.的最小值为.
(3)如图5中,将绕点逆时针旋转得到,则易知是等边二角形,作于,交于,则即为所求的最小值.
易知,的最小值为.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第六节:费马点最值模型
129.正方形中的费马点最值问题
如图,点是正方形内一点,并延长与相交于点.
(1)若,求的大小;
(2)若的最小值为,请直接写出正方形的边长.
130.费马点最值问题压轴题
如图,Rt中,,点是边上一动点,连接,把绕点逆时针旋转,得到,连接.点是的中点,连接.
(1)求证:;
(2)如图2所示,在点运动的过程中,当时,分别延长,相交于点,猜想与存在的数量关系,并证明你猜想的结论;
(3)在点运动的过程中,在线段上存在一点,使的值最小.当的值取得最小值时,的长为,请直接用含的式子表示的长.
131.已知费马点最值求正方形的边长
如图,四边形是正方形,是等边三角形,为对角线(不含点)上任意一点,将绕点逆时针旋转得到,连接.
(1)求证:;
(2)①当点在何处时,的值最小;
②当点在何处时,的值最小,并说明理由;
(3)当的最小值为时,求正方形的边长.
132.图形操作探究和拓展应用费马点最值问题
(1)【操作发现】如图1,将绕点顺时针旋转,得到,连接,则_________度.
(2)【类比探究】如图2,在等边三角形内任取一点,连接,求证:以的长为三边必能组成三角形.
(3)【解决问题】如图3,在边长为的等边三角形内有一点,求的面积.
(4)【拓展应用】如图4是A,B,C三个村子位置的平面图,经测量,为内的一个动点,连接.求的最小值.
133.从特例探究到拓展费马点最值问题
小颖在学习“两点之间线段最短”查阅资料时发现:内总存在一点与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点为等边的中心,将绕点逆时针旋转得到,从而有,连接得到,同时,,即四点共线,故.在中,另取一点,易知点与三个顶点连线的夹角不相等,可证明、四点不共线,所以,即点到三个顶点距离之和最小.
【探究】(1)如图2,为内一点,,证明的值最小;
【拓展】(2)如图3,中,,且点为内一点,求点到三个顶点的距离之和的最小值.
134.费马点最值模型的生产实践应用题
【问题情境】如图1,在中,,则的外接圆的半径值为_________.
【问题解决】如图2,点为正方形内一点,且,若,求AP的最小值.
【问题解决】如图3,正方形是一个边长为的隔离区域设计图,为大门,点在边上,,点是正方形内设立的一个活动岗哨,到的张角为,即,点为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点,使得到三个岗哨的距离和最小,试求的最小值.(保留根号或结果精确到,参考数据).
135.费马点模型的问题探究与应用
问题探究:将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换.旋转变换是几何变换的一种基本模型.经过旋转,往往能使图形的几何性质明白显现.题设和结论中的元素由分散变为集中,相互之间的关系清楚明了,从而将求解问题灵活转化.
问题提出:如图1,是边长为1的等边三角形,为内部一点,连接,求的最小值.
方法分析:通过转化,把由三角形内一点发出的三条线段(星型线)转化为两定点之间的折线(化星为折),再利用“两点之间线段最短”求最小值(化折为直).
问题解决:如图2,将绕点逆时针旋转至,连接PP',记与交于点,易知.由,可知为正三角形,有.
故.因此,当共线时,有最小值是.
学以致用:
(1)如图3,在中,为内部一点,连接,则的最小值是_________.
(2)如图4,在中,为内部一点,连接,求的最小值.
(3)如图5,是边长为2的正方形内一点,为边上一点,连接、,求的最小值.
答案
129.解(1)如图1,将绕点逆时针旋转得
,,
,
,,
.
(2).如图2,将绕点顺时针旋转得,连接,作交的延长线于.
当四点共线时,最小,这个最小值就是线段的长.,
是等边三角形,,设正方形边长为,Rt中,,,
在Rt中,,,
正方形边长为2.
130.证明:(1),
,把绕点逆时针旋转,得到,
,又,,
点是的中点,;
(2),理由如下:如下图,连接,由(1)可知,,又,
四点共圆,连接
四点共圆,
是等腰直角三角形,又
,又,
(3).如下图,将绕点顺时针旋转得到,连接,
是等边三角形,,
当四点共线时,值最小,此时,连接,即为的最小值.
连接,将绕点顺时针旋转得到,,
是等边三角形,是等边三角形,,
垂直平分,,
,
,由(1)可知:.
131.(1)证明:是等边二角形,.,
.即.又.
(2)【解】①当点落在的中点时,三点共线,的值最小.
②如图,连接,当点位于与的交点处时,的值最小,理由如下:连接,
由(1)知,,是等边三角形..
.根据“两点之间线段最短”可知,
若在同一条直线上时,取得最小值,最小值为.
在和中,易证(SAS),,
若连接,则,
可以同时在直线上.当点位于与的交点处时,的值最小,即等于的长.
(3)【解】过点作交的延长线于,.
设正方形的边长为,则.在Rt中,,
.解得(舍去负值).正方形的边长为.
132.(1)【操作发现】【解】如图,连接.
绕点顺时针旋转,得到,
是等边三角形,
故答案为60.
(2)【类比探究】证明:如图2中,以为边长作等边,使分别在的两侧,连接.
,
,
,在中,,
又的长为三边必能组成三角形.
(3)【解决问题】【解】如图3中,将绕点按逆时针方向旋转,得到是等边三角形,,,即,即,.(4)【拓展应用】【解】如图4中,将绕点顺时针旋转,得到,连接,则,.
将绕点顺时针旋转,得到,(旋转的性质),,是等边三角形,
当BPDE四点共线时,有最小值,BE即为所求.,
,,
在Rt中,,,
的最小值为;
133.【解】(1).如图2,将绕点逆时针旋转得到
为等边三角形,
,,
即四点共线,的值最小.
(2).【解】如图3,将绕点,顺时针旋转,得,易得即为所求的最小值。
在Rt中,
134.【解】(1)如图1,作的外接圆,作直径,连接是等边三角形,,设与交于点,在直角三角形中,,故答案为:5;
(2)如图2,点在以为直径的圆上,设圆心为点,则,
三点线时最小,在直角三角形中,,
的最小值为:;
(3)如图3,设所在圆的圆心为点,根据(1)可得所在圆的半径为,以点为旋转中心,将顺时针旋转,得到,当,共线时,最小,即为所求.过点作交的延长线于点,连接,则是等边三角形,过点作于交于点,连接,
四边形是正方形,,,
,是等边三形,
且,
,,
,最小值为:.
135.【解】(1)如图3,将绕点逆时针,旋转得到,易知是等边三角形,,
在Rt中,,
即为所求的最小值.的最小值为5.故答案为5.
(2)如图4中,将绕点逆时针旋转,得到,易知是等腰直角三角形,,作交的延长线于.在中,
,在Rt中,,,
即为所求的最小值.的最小值为.
(3)如图5中,将绕点逆时针旋转得到,则易知是等边二角形,作于,交于,则即为所求的最小值.
易知,的最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
