【中考数学几何模型】第七节:其它类型几何最值常考题136-145(含答案)
文档属性
| 名称 | 【中考数学几何模型】第七节:其它类型几何最值常考题136-145(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 10:11:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第七节:其它类型几何最值常考题
136.二次函数抛物线上的动点矩形的性质(初三)
如图,在平面直角坐标系中,点在抛物线上运动,过点作轴于点,以为对角线作矩形,连接,则对角线的最小值为( )
A.1
B.2
C.
D.
137.圆和直角三角形相切双动点最值问题(初三)
如图,在中,,以边的中点0为圆心,作半圆与相切,点分别是边和半圆上的动点,连接,则长的最大值与最小值的和是( )
A.9
B.10
C.
D.
138.动直线双垂直用构造法求最值问题(初二)
如图,在中,是的中点,直线1经过点,垂足分别为,则的最大值为( )
A.
B.
C.
D.
139.动点可能性探索求最值选择压轴题(初三)
如图,等边的边长为3,点在边上,,线段在边上运动,,有下列结论:(1)与可能相等;(2)与可能相似;(3)四边形面积的最大值为;(4)四边形周长的最小值为.其中,正确结论的序号为( )
A.(1)(4)
B.(2)(4)
C.(1)(3)
D.(2)(3)
140.梯子问题,取斜边的中点求最值问题(初二)
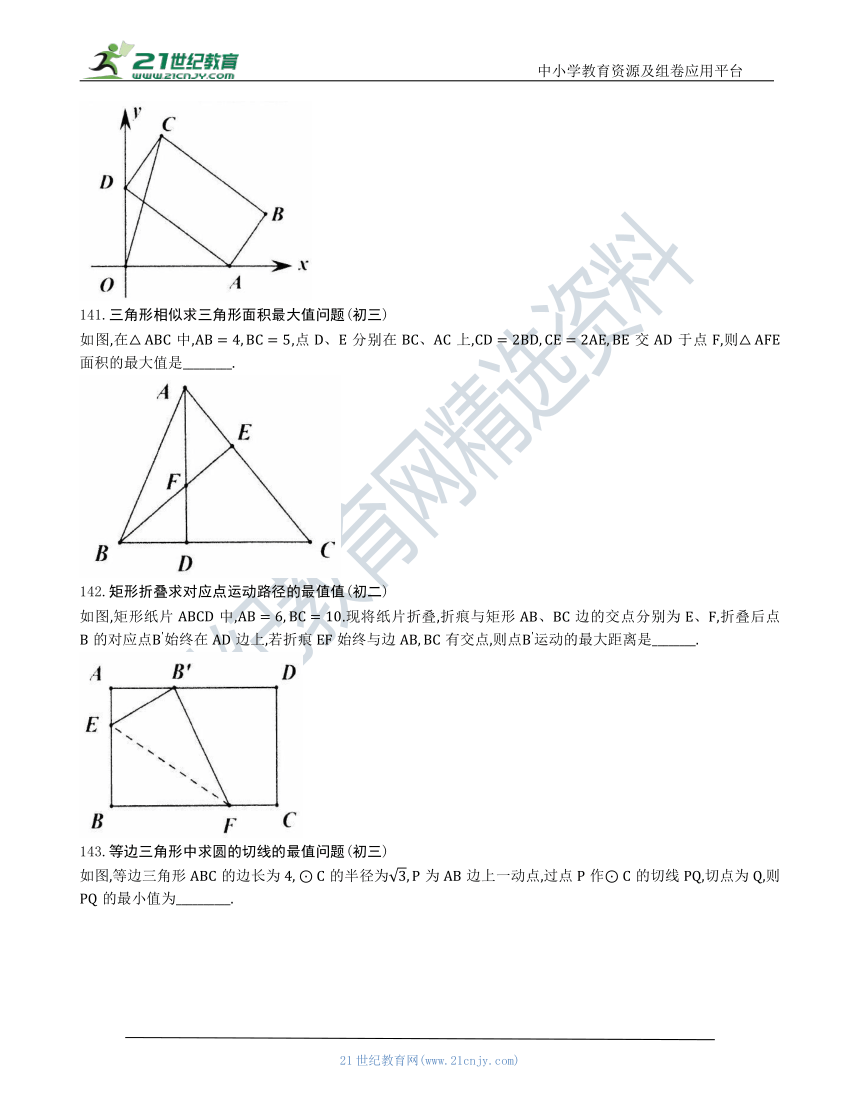
如图,矩形,点在轴正半轴上,点在轴正半轴上.当点在轴上运动时,点也随之在轴上运动,在这个运动过程中,点到原点0的最大距离为_________.
141.三角形相似求三角形面积最大值问题(初三)
如图,在中,,点分别在上,交于点,则面积的最大值是_________.
142.矩形折叠求对应点运动路径的最值值(初二)
如图,矩形纸片中,.现将纸片折叠,折痕与矩形边的交点分别为,折叠后点的对应点始终在边上,若折痕始终与边有交点,则点运动的最大距离是________.
143.等边三角形中求圆的切线的最值问题(初三)
如图,等边三角形的边长为的半径为为边上一动点,过点作的切线,切点为,则的最小值为__________.
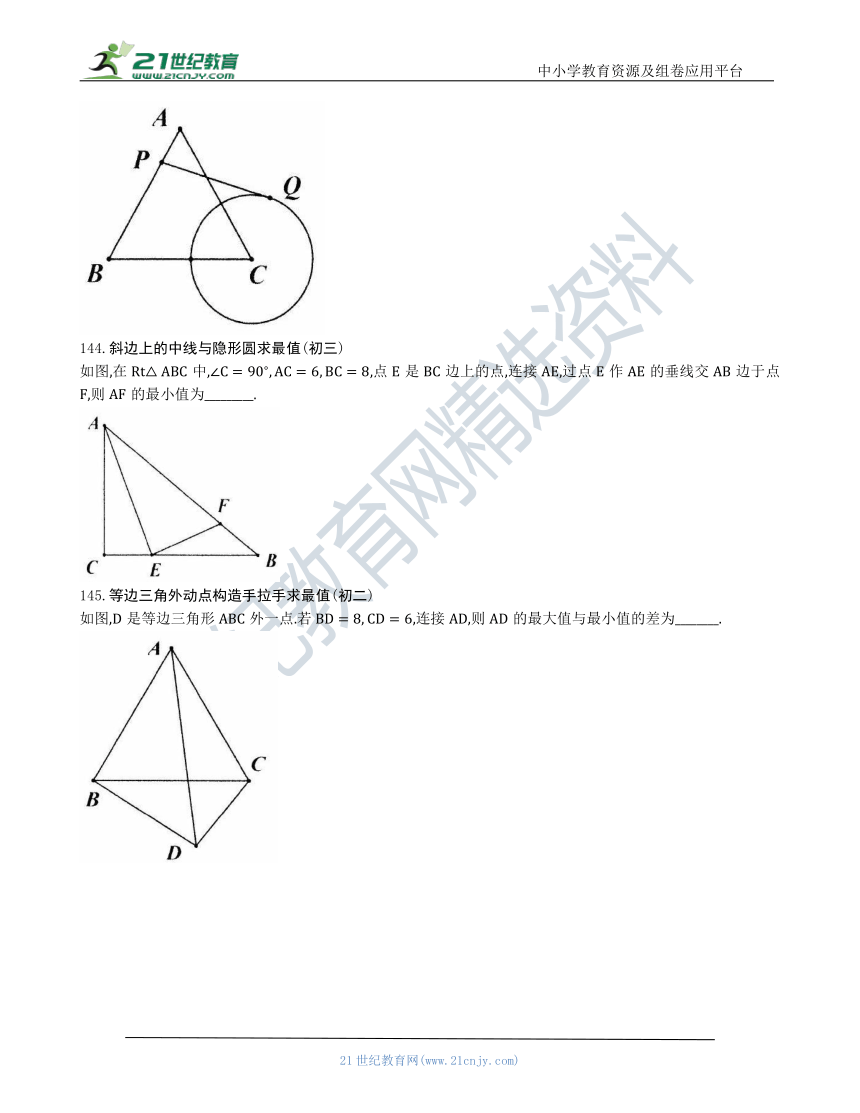
144.斜边上的中线与隐形圆求最值(初三)
如图,在Rt中,,点是边上的点,连接,过点作的垂线交边于点,则的最小值为_________.
145.等边三角外动点构造手拉手求最值(初二)
如图,是等边三角形外一点.若,连接,则的最大值与最小值的差为________.
答案
136.【解】抛物线的顶点坐标为四边形为矩形,,
而轴,的长等于点的纵坐标,
当点在抛物线的顶点时,点到轴的距离最小,最小值为对角线的最小值为2.故选:.
137.【解】如图,设与相切于点,连接,作垂足为交于,此时垂线段最短,最小值为,,
,最小值为,
如图,当在边上时,与重合时,经过圆心,经过圆心的弦最长,最大值,
长的最大值与最小值的和是9.故选:.
138.【解】如图,过点作于点,过点作于点,在Rt中,,
,在Rt中,,
点为中点,,在与中,易证,延长,过点作于点,可得,在Rt中,,当直线时,最大值为,综上所述,的最大值为.故选:.
139.【解】(1)利用图象法可知,或通过计算可知的最大值为的最小值为,所以,故(1)错误.
(2)设,当或时,与相似,即或,解得或或当或或时,两个三角形相似,故(2)正确
(3)设,则四边形的面积
的最大值为时,四边形的面积最大,最大值,故(3)正确,
四边形中,当的值最小值时,四边形的周长有最小值.如图,作点关于的对称点作,再截取,得,
当F、P、C三点共线,即为的最小值。
由题意,,,
,,
四边形的周长的最小值,故(4)错误,故选:(2)(3)正确,选.
140.【解】如图,取的中点,连接矩形,
点是的中点,,
,点是的中点,,在中,,当点在上时,,的最大值为,故答案为:.
141.【解】连接,,
,,
,
当时,的面积最大,最大值,
的面积的最大值,故答案为:.
142.【解】当与重合时,如图1,由折叠得:四边形是矩形,,
,在Rt中,;
当与重合时,如图2,由折叠得:,综上所述,的取值范围是:,
点运动的最大距离为.故答案为4.
143.【解】连接,作于,如图,
等边三角形的边长为
,
为的切线,
,在Rt中,,当最小时,有最小值.
点是边上一动点,当点运动到点时,最小,即的最小值为,
的最小值为,故答案为:3.
144.【解】以为直径画圆,当圆与相切于点时,的值最小,
是圆的切线,,
,,设,在Rt中,,解得,的最小值为,故答案为.
145.【解】如图1,以为边作等边,连接,和是等边三角形,
,
,
在和中,易证,
,
,即,
.
则当三点共线时,可得的最大值(如图2)是14,与最小值(如图3)别为2.
的最大值与最小值的差为.
故答案为:12.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第七节:其它类型几何最值常考题
136.二次函数抛物线上的动点矩形的性质(初三)
如图,在平面直角坐标系中,点在抛物线上运动,过点作轴于点,以为对角线作矩形,连接,则对角线的最小值为( )
A.1
B.2
C.
D.
137.圆和直角三角形相切双动点最值问题(初三)
如图,在中,,以边的中点0为圆心,作半圆与相切,点分别是边和半圆上的动点,连接,则长的最大值与最小值的和是( )
A.9
B.10
C.
D.
138.动直线双垂直用构造法求最值问题(初二)
如图,在中,是的中点,直线1经过点,垂足分别为,则的最大值为( )
A.
B.
C.
D.
139.动点可能性探索求最值选择压轴题(初三)
如图,等边的边长为3,点在边上,,线段在边上运动,,有下列结论:(1)与可能相等;(2)与可能相似;(3)四边形面积的最大值为;(4)四边形周长的最小值为.其中,正确结论的序号为( )
A.(1)(4)
B.(2)(4)
C.(1)(3)
D.(2)(3)
140.梯子问题,取斜边的中点求最值问题(初二)
如图,矩形,点在轴正半轴上,点在轴正半轴上.当点在轴上运动时,点也随之在轴上运动,在这个运动过程中,点到原点0的最大距离为_________.
141.三角形相似求三角形面积最大值问题(初三)
如图,在中,,点分别在上,交于点,则面积的最大值是_________.
142.矩形折叠求对应点运动路径的最值值(初二)
如图,矩形纸片中,.现将纸片折叠,折痕与矩形边的交点分别为,折叠后点的对应点始终在边上,若折痕始终与边有交点,则点运动的最大距离是________.
143.等边三角形中求圆的切线的最值问题(初三)
如图,等边三角形的边长为的半径为为边上一动点,过点作的切线,切点为,则的最小值为__________.
144.斜边上的中线与隐形圆求最值(初三)
如图,在Rt中,,点是边上的点,连接,过点作的垂线交边于点,则的最小值为_________.
145.等边三角外动点构造手拉手求最值(初二)
如图,是等边三角形外一点.若,连接,则的最大值与最小值的差为________.
答案
136.【解】抛物线的顶点坐标为四边形为矩形,,
而轴,的长等于点的纵坐标,
当点在抛物线的顶点时,点到轴的距离最小,最小值为对角线的最小值为2.故选:.
137.【解】如图,设与相切于点,连接,作垂足为交于,此时垂线段最短,最小值为,,
,最小值为,
如图,当在边上时,与重合时,经过圆心,经过圆心的弦最长,最大值,
长的最大值与最小值的和是9.故选:.
138.【解】如图,过点作于点,过点作于点,在Rt中,,
,在Rt中,,
点为中点,,在与中,易证,延长,过点作于点,可得,在Rt中,,当直线时,最大值为,综上所述,的最大值为.故选:.
139.【解】(1)利用图象法可知,或通过计算可知的最大值为的最小值为,所以,故(1)错误.
(2)设,当或时,与相似,即或,解得或或当或或时,两个三角形相似,故(2)正确
(3)设,则四边形的面积
的最大值为时,四边形的面积最大,最大值,故(3)正确,
四边形中,当的值最小值时,四边形的周长有最小值.如图,作点关于的对称点作,再截取,得,
当F、P、C三点共线,即为的最小值。
由题意,,,
,,
四边形的周长的最小值,故(4)错误,故选:(2)(3)正确,选.
140.【解】如图,取的中点,连接矩形,
点是的中点,,
,点是的中点,,在中,,当点在上时,,的最大值为,故答案为:.
141.【解】连接,,
,,
,
当时,的面积最大,最大值,
的面积的最大值,故答案为:.
142.【解】当与重合时,如图1,由折叠得:四边形是矩形,,
,在Rt中,;
当与重合时,如图2,由折叠得:,综上所述,的取值范围是:,
点运动的最大距离为.故答案为4.
143.【解】连接,作于,如图,
等边三角形的边长为
,
为的切线,
,在Rt中,,当最小时,有最小值.
点是边上一动点,当点运动到点时,最小,即的最小值为,
的最小值为,故答案为:3.
144.【解】以为直径画圆,当圆与相切于点时,的值最小,
是圆的切线,,
,,设,在Rt中,,解得,的最小值为,故答案为.
145.【解】如图1,以为边作等边,连接,和是等边三角形,
,
,
在和中,易证,
,
,即,
.
则当三点共线时,可得的最大值(如图2)是14,与最小值(如图3)别为2.
的最大值与最小值的差为.
故答案为:12.
21世纪教育网(www.21cnjy.com)
同课章节目录
