【中考数学几何模型】第九节:半角模型184-194(含答案)
文档属性
| 名称 | 【中考数学几何模型】第九节:半角模型184-194(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 441.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 10:40:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第九节:半角模型
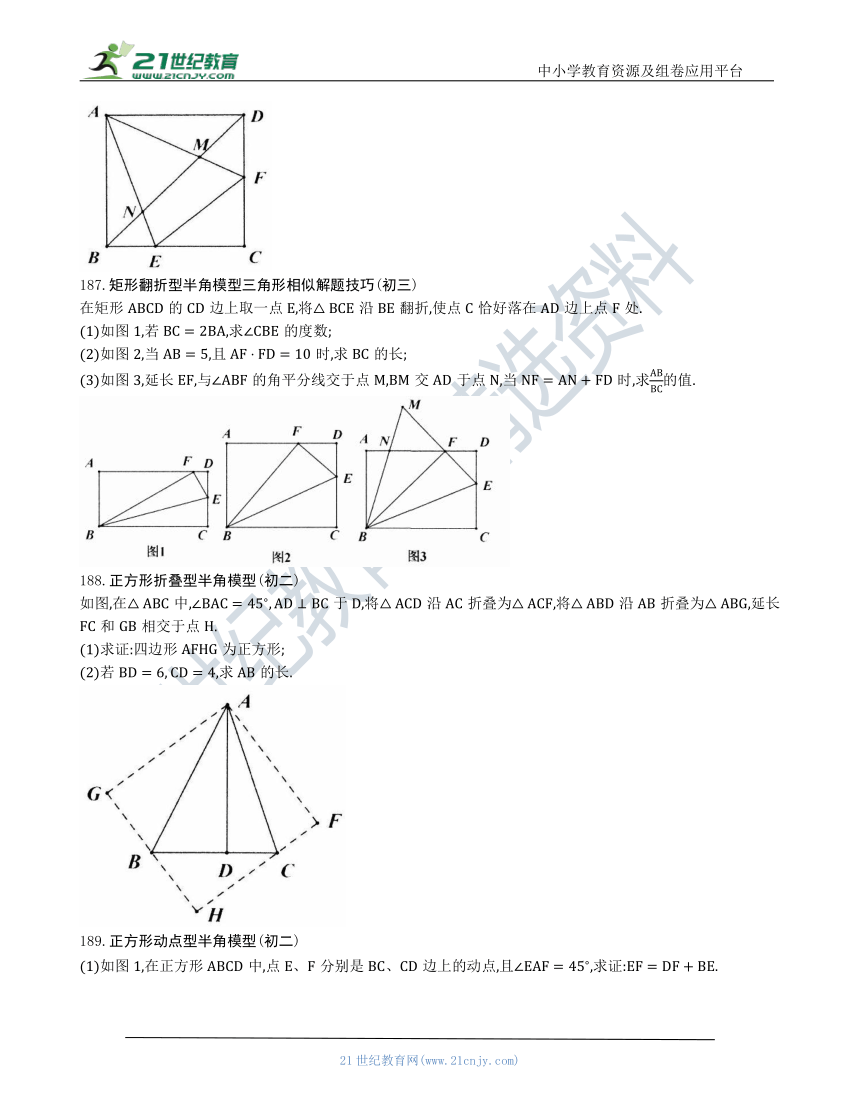
184.等腰直角三角形中的半角模型结论(初二)
在中,,,点和点均在边上,且,试猜想BD、DE、EC应满足的数量关系,并写出推理过程.
185.等腰直角三角形中的半角模型结论三角函数(初三)
如图①,是等腰Rt的斜边上的两动点,且.
(1)求证:;
(2)求证:;
(3)如图②,作,垂足为,设,
不妨设,请利用(2)的结论证明:当时,成立.
186.正方形中的半角模型证明过程(初二)
如图,在正方形中,点分别在边上,且,分别连接与分别相交于点
(1)求证:.为了证明“”,小明延长至点,使,连接AG,请画出辅助线并按小明的思路写出证明过程.
(2)若,请求出正方形的边长.
(3)请直接写出线段BN、MN、DM三者之间的数量关系
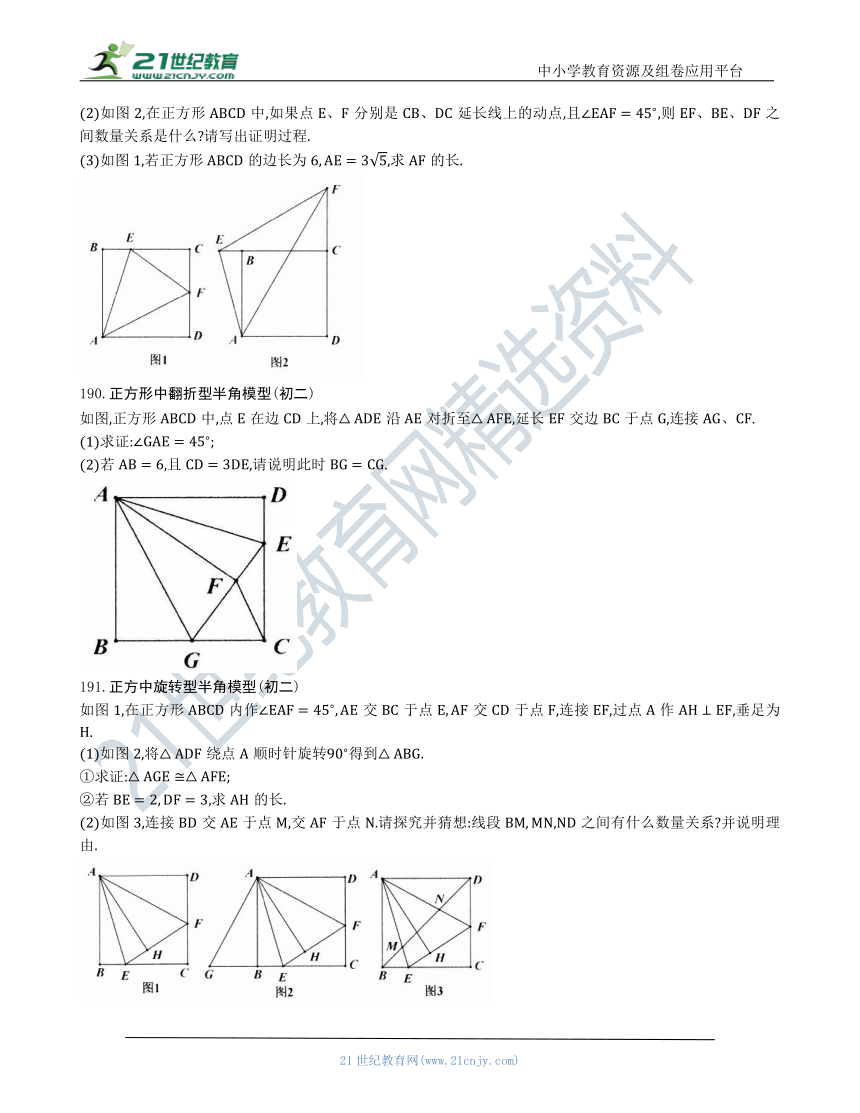
187.矩形翻折型半角模型三角形相似解题技巧(初三)
在矩形的边上取一点,将沿翻折,使点恰好落在边上点处.
(1)如图1,若,求的度数;
(2)如图2,当,且时,求的长;
(3)如图3,延长,与的角平分线交于点,交于点,当时,求的值.
188.正方形折叠型半角模型(初二)
如图,在中,于,将沿折叠为,将沿折叠为,延长和相交于点.
(1)求证:四边形为正方形;
(2)若,求的长.
189.正方形动点型半角模型(初二)
(1)如图1,在正方形中,点分别是边上的动点,且,求证:.
(2)如图2,在正方形中,如果点分别是延长线上的动点,且,则之间数量关系是什么 请写出证明过程.
(3)如图1,若正方形的边长为,求的长.
190.正方形中翻折型半角模型(初二)
如图,正方形中,点在边上,将沿对折至,延长交边于点,连接.
(1)求证:;
(2)若,且,请说明此时.
191.正方中旋转型半角模型(初二)
如图1,在正方形内作交于点交于点,连接,过点作,垂足为.
(1)如图2,将绕点顺时针旋转得到.
①求证:;
②若,求的长.
(2)如图3,连接交于点,交于点.请探究并猜想:线段,ND之间有什么数量关系 并说明理由.
192.筝形中的半角模型的类比探究和应用(初二)
旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)尝试解决:如图①,在等腰Rt中,,点是上的一点,,将绕点旋转后得到,连接,则
(2)类比探究:如图②,在“筝形”四边形中,于点于点,点分别是上的点,且,求的周长.(结果用a表示)
(3)拓展应用:如图③,已知四边形,,求四边形的面积.
193.等腰三角形中的半角模型结论探究(初二)
已知在是边上的点,将绕点旋转,得到,连接.
(1)如图1,当,求证:;
(2)如图2,与有怎样的数量关系 请你写出这个关系,并说明理由;
(3)如图3,在(2)的结论下,当添加“”条件时,判断形状,并加以证明.
194.从正方形半角模型到矩形的半角模型(初三)
问题提出:(1)如图①,已知在边长为10的等边中,点在边上,,连接,则的面积为________;
问题探究:(2)如图②已知在边长为6的正方形中,点在边上,点在边上,且.若,求的面积;
问题解决:(3)如图③是某座城市延康大道的一部分,因自来水抢修需在4米,米的矩形区域内开挖一个的工作面,其中分别在边上(不与重合),且,为了减少对该路段的拥堵影响,要求面积最小,那么是否存在一个面积最小的 若存在,请求出面积的最小值;若不存在,请说明理由.
答案
184.【解】,理由是:把绕点顺时针旋转至,可使与重合,连接在Rt中,,,,在和中,(SAS),,在Rt中,由勾股定理得:,即.
185.证明:(1)是等腰直角三角形,
,
,
,在和
中,
(2)由(1)知,,
,
,,在Rt中,根据勾股定理得,,
;
(3)在Rt中,,
,
,
由(2)知,,
,
,
在Rt中,,
在Rt中,,
右边,
,
左边,
左边=右边,即当时,
成立.
186.(1)证明:如图1,延长至点,使,连接四边形为正方形,
,在和中,
,在和中,(SAS),
;
(2)【解】设正方形的边长为,
,
由(1)得:,Rt中,,,
解得:或-1(舍),答:正方形的边长为6.
(3)【解】;理由是:
如图2,在上截取,连接,
在和中,
AMD(SAS),,
又.在和中,,
(SAS),.
187.【解】(1)四边形是矩形,,
将沿翻折,使点恰好落在边上点处,
,
,
四边形是矩形,,
;
(2)将沿翻折,使点恰好落在边上点
处,,
又矩形中,,
,
,
,
,,
.
(3)如图,过点作于点,
,
,
,
设平分,
,设,则,
,
解得.
.
图3
188.证明:(1);由折叠可知,,
;
;
四边形是正方形,
(2)四边形是正方形,,
又;
设的长为,则4.在Rt中,,
解得(不合题意,舍去),
.
189.证明:(1)把绕点顺时针旋转至,如图1,,
,
;
(2)结论:;证明:如图2,将绕点顺时针旋转至AM,,;
(3)如图1,由(1)可得
,
,
.
190.【解】(1)四边形为正方形,
;由题意得:
,
;
在Rt与Rt中,,
,
.
(2)设,则;
;由勾股定理得:,
即,解得:,
.
191.【解】(1)(1)由旋转的性质可知:,
.四边形为正方形,
.又,
.
.在和中,
(2),
.设正方形的边长为,
则.在Rt中,由勾股定理得:
,即.
解得:.
(2)如上图:将逆时针旋转得.
四边形为正方形,.由旋转的性质可知:.
.
在和中,
.
又.
192.【解】(1),由旋转得:,
是等腰直角三角形,
,
;故答案为:;
(2)如图2,延长到,使,连接,
,
,在和中,
,
在和中,,
(SAS),,
的周长
(3)如图3,连接,将绕点顺时针方向旋转,得到,连接,延长,作于,由旋转得:,
,是等边三角形,
,
,
,
,
设等边三角形的高为,则勾股定理得:,
.
193.(1)证明:绕点旋转得到,
,
,
在和中,
;
(2)【解】.理由如下:
在和中,,
,
;
(3)【解】是等腰直角三角形;
证明:,
,
,
由(2)知,,
绕点旋转得到,
,
在Rt中,,
,
是等腰直角三角形.
194.【解】(1)如图1,过点作于,
为等边三角形,,
的面积,故答案为:;
图1
图2
(2)如图2,将绕点顺时针旋转得到,由旋转的性质得,,
,
在和中,,
,
;
图3
(3)把绕点顺时针旋转并缩小为,得到,则,过点作于于,
,
,设的外接圆圆心为0,连接、,过得0作于,则,设的外接圆的半径为,则,
由题意得,,即,解得,,
的面积,
的面积的最小值为,
的面积的冣小值为.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第九节:半角模型
184.等腰直角三角形中的半角模型结论(初二)
在中,,,点和点均在边上,且,试猜想BD、DE、EC应满足的数量关系,并写出推理过程.
185.等腰直角三角形中的半角模型结论三角函数(初三)
如图①,是等腰Rt的斜边上的两动点,且.
(1)求证:;
(2)求证:;
(3)如图②,作,垂足为,设,
不妨设,请利用(2)的结论证明:当时,成立.
186.正方形中的半角模型证明过程(初二)
如图,在正方形中,点分别在边上,且,分别连接与分别相交于点
(1)求证:.为了证明“”,小明延长至点,使,连接AG,请画出辅助线并按小明的思路写出证明过程.
(2)若,请求出正方形的边长.
(3)请直接写出线段BN、MN、DM三者之间的数量关系
187.矩形翻折型半角模型三角形相似解题技巧(初三)
在矩形的边上取一点,将沿翻折,使点恰好落在边上点处.
(1)如图1,若,求的度数;
(2)如图2,当,且时,求的长;
(3)如图3,延长,与的角平分线交于点,交于点,当时,求的值.
188.正方形折叠型半角模型(初二)
如图,在中,于,将沿折叠为,将沿折叠为,延长和相交于点.
(1)求证:四边形为正方形;
(2)若,求的长.
189.正方形动点型半角模型(初二)
(1)如图1,在正方形中,点分别是边上的动点,且,求证:.
(2)如图2,在正方形中,如果点分别是延长线上的动点,且,则之间数量关系是什么 请写出证明过程.
(3)如图1,若正方形的边长为,求的长.
190.正方形中翻折型半角模型(初二)
如图,正方形中,点在边上,将沿对折至,延长交边于点,连接.
(1)求证:;
(2)若,且,请说明此时.
191.正方中旋转型半角模型(初二)
如图1,在正方形内作交于点交于点,连接,过点作,垂足为.
(1)如图2,将绕点顺时针旋转得到.
①求证:;
②若,求的长.
(2)如图3,连接交于点,交于点.请探究并猜想:线段,ND之间有什么数量关系 并说明理由.
192.筝形中的半角模型的类比探究和应用(初二)
旋转是一种重要的图形变换,当图形中有一组邻边相等时往往可以通过旋转解决问题.
(1)尝试解决:如图①,在等腰Rt中,,点是上的一点,,将绕点旋转后得到,连接,则
(2)类比探究:如图②,在“筝形”四边形中,于点于点,点分别是上的点,且,求的周长.(结果用a表示)
(3)拓展应用:如图③,已知四边形,,求四边形的面积.
193.等腰三角形中的半角模型结论探究(初二)
已知在是边上的点,将绕点旋转,得到,连接.
(1)如图1,当,求证:;
(2)如图2,与有怎样的数量关系 请你写出这个关系,并说明理由;
(3)如图3,在(2)的结论下,当添加“”条件时,判断形状,并加以证明.
194.从正方形半角模型到矩形的半角模型(初三)
问题提出:(1)如图①,已知在边长为10的等边中,点在边上,,连接,则的面积为________;
问题探究:(2)如图②已知在边长为6的正方形中,点在边上,点在边上,且.若,求的面积;
问题解决:(3)如图③是某座城市延康大道的一部分,因自来水抢修需在4米,米的矩形区域内开挖一个的工作面,其中分别在边上(不与重合),且,为了减少对该路段的拥堵影响,要求面积最小,那么是否存在一个面积最小的 若存在,请求出面积的最小值;若不存在,请说明理由.
答案
184.【解】,理由是:把绕点顺时针旋转至,可使与重合,连接在Rt中,,,,在和中,(SAS),,在Rt中,由勾股定理得:,即.
185.证明:(1)是等腰直角三角形,
,
,
,在和
中,
(2)由(1)知,,
,
,,在Rt中,根据勾股定理得,,
;
(3)在Rt中,,
,
,
由(2)知,,
,
,
在Rt中,,
在Rt中,,
右边,
,
左边,
左边=右边,即当时,
成立.
186.(1)证明:如图1,延长至点,使,连接四边形为正方形,
,在和中,
,在和中,(SAS),
;
(2)【解】设正方形的边长为,
,
由(1)得:,Rt中,,,
解得:或-1(舍),答:正方形的边长为6.
(3)【解】;理由是:
如图2,在上截取,连接,
在和中,
AMD(SAS),,
又.在和中,,
(SAS),.
187.【解】(1)四边形是矩形,,
将沿翻折,使点恰好落在边上点处,
,
,
四边形是矩形,,
;
(2)将沿翻折,使点恰好落在边上点
处,,
又矩形中,,
,
,
,
,,
.
(3)如图,过点作于点,
,
,
,
设平分,
,设,则,
,
解得.
.
图3
188.证明:(1);由折叠可知,,
;
;
四边形是正方形,
(2)四边形是正方形,,
又;
设的长为,则4.在Rt中,,
解得(不合题意,舍去),
.
189.证明:(1)把绕点顺时针旋转至,如图1,,
,
;
(2)结论:;证明:如图2,将绕点顺时针旋转至AM,,;
(3)如图1,由(1)可得
,
,
.
190.【解】(1)四边形为正方形,
;由题意得:
,
;
在Rt与Rt中,,
,
.
(2)设,则;
;由勾股定理得:,
即,解得:,
.
191.【解】(1)(1)由旋转的性质可知:,
.四边形为正方形,
.又,
.
.在和中,
(2),
.设正方形的边长为,
则.在Rt中,由勾股定理得:
,即.
解得:.
(2)如上图:将逆时针旋转得.
四边形为正方形,.由旋转的性质可知:.
.
在和中,
.
又.
192.【解】(1),由旋转得:,
是等腰直角三角形,
,
;故答案为:;
(2)如图2,延长到,使,连接,
,
,在和中,
,
在和中,,
(SAS),,
的周长
(3)如图3,连接,将绕点顺时针方向旋转,得到,连接,延长,作于,由旋转得:,
,是等边三角形,
,
,
,
,
设等边三角形的高为,则勾股定理得:,
.
193.(1)证明:绕点旋转得到,
,
,
在和中,
;
(2)【解】.理由如下:
在和中,,
,
;
(3)【解】是等腰直角三角形;
证明:,
,
,
由(2)知,,
绕点旋转得到,
,
在Rt中,,
,
是等腰直角三角形.
194.【解】(1)如图1,过点作于,
为等边三角形,,
的面积,故答案为:;
图1
图2
(2)如图2,将绕点顺时针旋转得到,由旋转的性质得,,
,
在和中,,
,
;
图3
(3)把绕点顺时针旋转并缩小为,得到,则,过点作于于,
,
,设的外接圆圆心为0,连接、,过得0作于,则,设的外接圆的半径为,则,
由题意得,,即,解得,,
的面积,
的面积的最小值为,
的面积的冣小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
