1.1《探索勾股定理》同步练习(无答案)
文档属性
| 名称 | 1.1《探索勾股定理》同步练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 70.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-03 21:16:51 | ||
图片预览


文档简介
《探索勾股定理》同步练习
练习1
1.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2 B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
2.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90○,则(? )
A、b2= a2+ c2 B、c2= a2+ b2 C、a2+b2=c2 D、a+b=c
3.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是 ( )
?A、钝角三角形??B、锐角三角形? C、直角三角形?? D、等边三角形
4.一直角三角形的斜边长比一直角边长大,另一直角边长为,则斜边长为 (? )
A、4???? B、8??? C、10?? D、12
5、如图,中字母A所代表的正方形的面积为(?? )
A. 4????? B. 8? ? C. 16??? D. 64
6.一直角三角形的一条直角边长是7cm , 另一条直角边与斜边长的和是49cm , 则斜边的长( )
A. 18cm???? B. 20 cm??????C. 24 cm????? D. 25cm
7.直角三角形一直角边长为12,另两条边长均为自然数,则其周长为(? )
A.30?? B.28?? C.56? ? D.不能确定
8.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121??????B.120?? ? ???C.90?????? D.不能确定
练习2
1.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )?
A、 12米??????B、 13米????? C、 14米????? D、15米
2.如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
?A.6cm2????? B.8cm2???? C.10cm2??? D.12cm2
3.如图,下列各图中所示的线段的长度或正方形的面积为多少(各图中的三角形均为直角三角形)?
答:A=______,y=______,B=______
4.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=___.
5.如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米,则这棵大树折断前有__________米(保留到0.1米)。
6.在直角三角形ABC中,,两直角边分别为a,b,斜边为c,如果a=5,b=12,那么c=______;如果b=8,c=17,那么三角形的面积是______.
7.已知直角三角形三边长分别为3、4、x,则x=_____.
9.一个三角形三边之比是,则按角分类它是???? 三角形.
10.若三角形的三个内角的比是,最短边长为,最长边长为,则这个三角形三个角度数分别是????? ,另外一边的平方是????? .
11.在直角三角形中,______.
12.如图,已知中,,,,以直角边为直径作半圆,则这个半圆的面积是???? .
13.在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB=___________。
14.在△ABC中,∠C=90°,若c=10,a∶b=3∶4,则ab= .
练习3
1.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___.
2.有两棵树,一棵高6米,另一棵高3米,两树相距4米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了___米.
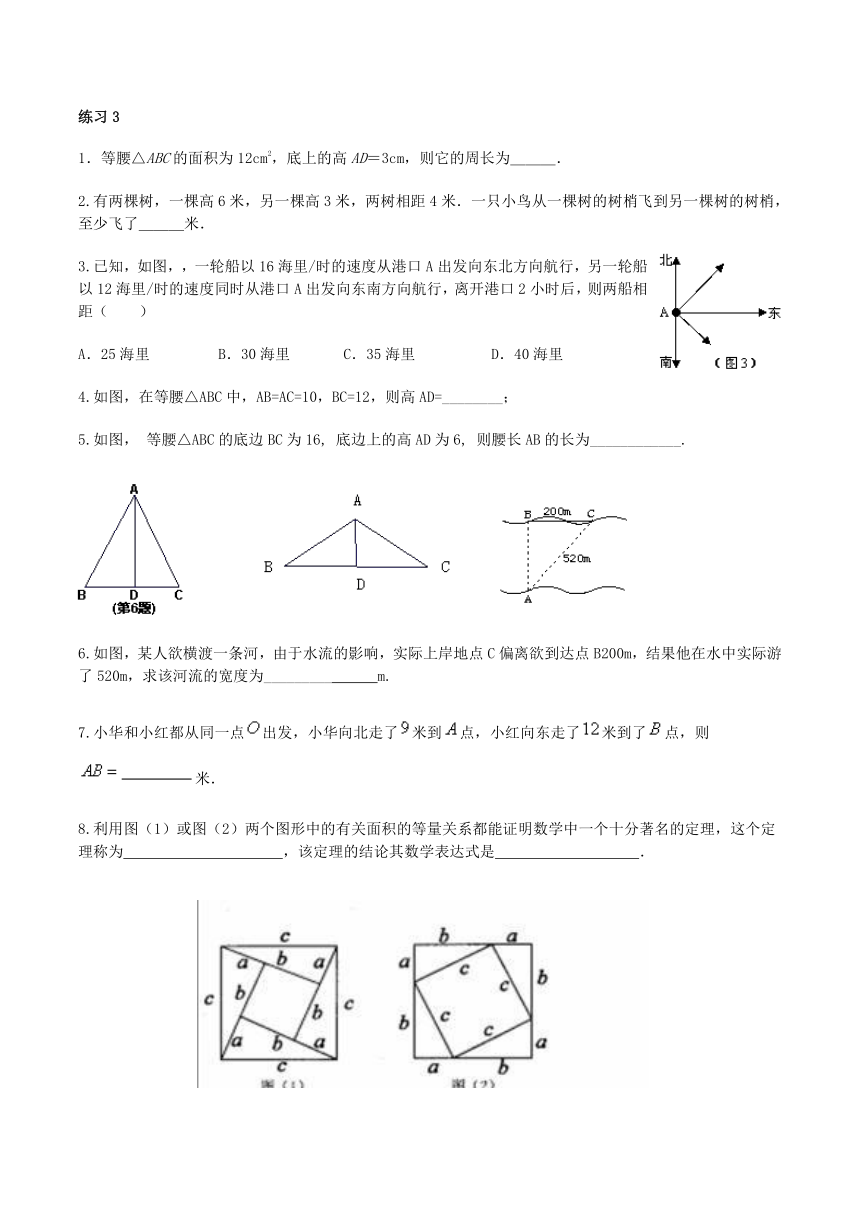
3.已知,如图,,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里???? B.30海里?? C.35海里?????D.40海里
4.如图,在等腰△ABC中,AB=AC=10,BC=12,则高AD=________;
5.如图, 等腰△ABC的底边BC为16, 底边上的高AD为6, 则腰长AB的长为____________.
6.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为_________ m.
7.小华和小红都从同一点出发,小华向北走了米到点,小红向东走了米到了点,则米.
8.利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为?????????? ,该定理的结论其数学表达式是????????? .
练习4
1.某菜农要修建一个塑料大棚,如图所示,若棚宽a=4m,高b=3m,长d=40m。
求覆盖在顶上(如右图阴影部分)的逆料薄膜的面积。
2.如图,已知直角三角形的两直角边的长分别为4cm,3cm,求斜边上的高的长.
3.如图,,AB=20,AD=8,BE=12,C为AB上一点,且DC=CE,求AC.
1.1《探索勾股定理》课后作业
练习1
1.如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
?
2.如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米。
①求梯子顶端与地面的距离OA的长。
②若梯子顶点A下滑1米到C点,求梯子的底端向右滑到D的距离。
3.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
?
练习2
1.(2013贵州省黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为( )
A.
5
B.
C.
D.
5或
2.(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
3.(2013湖南张家界)如图,OP=1,过P作PP1⊥OP,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2012= .
4.(2012重庆)如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
5.如图,矩形纸片ABCD的长AD=9 cm,宽AB=3 cm,将其折叠,使点D与点B重合,那么折叠后DE的长是多少?
练习1
1.下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2 B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
2.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=90○,则(? )
A、b2= a2+ c2 B、c2= a2+ b2 C、a2+b2=c2 D、a+b=c
3.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是 ( )
?A、钝角三角形??B、锐角三角形? C、直角三角形?? D、等边三角形
4.一直角三角形的斜边长比一直角边长大,另一直角边长为,则斜边长为 (? )
A、4???? B、8??? C、10?? D、12
5、如图,中字母A所代表的正方形的面积为(?? )
A. 4????? B. 8? ? C. 16??? D. 64
6.一直角三角形的一条直角边长是7cm , 另一条直角边与斜边长的和是49cm , 则斜边的长( )
A. 18cm???? B. 20 cm??????C. 24 cm????? D. 25cm
7.直角三角形一直角边长为12,另两条边长均为自然数,则其周长为(? )
A.30?? B.28?? C.56? ? D.不能确定
8.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )
A.121??????B.120?? ? ???C.90?????? D.不能确定
练习2
1.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )?
A、 12米??????B、 13米????? C、 14米????? D、15米
2.如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
?A.6cm2????? B.8cm2???? C.10cm2??? D.12cm2
3.如图,下列各图中所示的线段的长度或正方形的面积为多少(各图中的三角形均为直角三角形)?
答:A=______,y=______,B=______
4.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=___.
5.如图,今年第8号台风“桑美”是50多年以来登陆我国大陆地区最大的一次台风,一棵大树受“桑美”袭击于离地面5米处折断倒下,倒下部分的树梢到树的距离为7米,则这棵大树折断前有__________米(保留到0.1米)。
6.在直角三角形ABC中,,两直角边分别为a,b,斜边为c,如果a=5,b=12,那么c=______;如果b=8,c=17,那么三角形的面积是______.
7.已知直角三角形三边长分别为3、4、x,则x=_____.
9.一个三角形三边之比是,则按角分类它是???? 三角形.
10.若三角形的三个内角的比是,最短边长为,最长边长为,则这个三角形三个角度数分别是????? ,另外一边的平方是????? .
11.在直角三角形中,______.
12.如图,已知中,,,,以直角边为直径作半圆,则这个半圆的面积是???? .
13.在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB=___________。
14.在△ABC中,∠C=90°,若c=10,a∶b=3∶4,则ab= .
练习3
1.等腰△ABC的面积为12cm2,底上的高AD=3cm,则它的周长为___.
2.有两棵树,一棵高6米,另一棵高3米,两树相距4米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了___米.
3.已知,如图,,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A.25海里???? B.30海里?? C.35海里?????D.40海里
4.如图,在等腰△ABC中,AB=AC=10,BC=12,则高AD=________;
5.如图, 等腰△ABC的底边BC为16, 底边上的高AD为6, 则腰长AB的长为____________.
6.如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为_________ m.
7.小华和小红都从同一点出发,小华向北走了米到点,小红向东走了米到了点,则米.
8.利用图(1)或图(2)两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为?????????? ,该定理的结论其数学表达式是????????? .
练习4
1.某菜农要修建一个塑料大棚,如图所示,若棚宽a=4m,高b=3m,长d=40m。
求覆盖在顶上(如右图阴影部分)的逆料薄膜的面积。
2.如图,已知直角三角形的两直角边的长分别为4cm,3cm,求斜边上的高的长.
3.如图,,AB=20,AD=8,BE=12,C为AB上一点,且DC=CE,求AC.
1.1《探索勾股定理》课后作业
练习1
1.如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,那么这只小鸟至少几秒才可能到达小树和伙伴在一起?
?
2.如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米。
①求梯子顶端与地面的距离OA的长。
②若梯子顶点A下滑1米到C点,求梯子的底端向右滑到D的距离。
3.如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
?
练习2
1.(2013贵州省黔西南州)一直角三角形的两边长分别为3和4.则第三边的长为( )
A.
5
B.
C.
D.
5或
2.(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .
3.(2013湖南张家界)如图,OP=1,过P作PP1⊥OP,得OP1=;再过P1作P1P2⊥OP1且P1P2=1,得OP2=;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依此法继续作下去,得OP2012= .
4.(2012重庆)如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)
5.如图,矩形纸片ABCD的长AD=9 cm,宽AB=3 cm,将其折叠,使点D与点B重合,那么折叠后DE的长是多少?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
