【中考数学几何模型】第十三节:折叠模型268-277(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十三节:折叠模型268-277(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 198.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 10:59:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十三节:折叠模型
268.直角三角形折叠求角度(初二)
如图,在中,是斜边上的中线,将沿对折,使点落在点处,线段与相交于点,则等于( )
A.
B.
C.
D.
269.平行四边形折叠求角度(初二)
如图,将 沿对角线折叠,使点落在点处,交于点,若,则为( )
A.
B.
C.
D.
270.矩形折叠求线段(初二)
如图,矩形中,为对角线,将矩形沿所在直线折叠,使点落在上的点处,点落在上的点处,连接.已知,则的长为( )
A.3
B.5
C.
D.
271.直角三角形折叠求线段长(初二)
如图,在Rt中,,,将边沿翻折,使点落在上的点处,再将边沿翻折,使点落在延长线上的点处,两条折痕与斜边分别交于点,则线段的长为( )
A.
B.
C.
D.
272.三角形折叠求距离(初二)
如图,在中,,点在边上,,连接.如果将沿直线翻折后,点的对应点为点,那么点到直线的距离为________.
273.矩形折叠等腰三角形存在性讨论(初二)
如图,在矩形中,分别是边上一点,,将沿翻折得,连接,当________时,是以为腰的等腰三角形.
274.直接三角形折叠求线段的长(初二初三)
如图,在Rt中,,点在线段上,且,是线段上的一点,连接,将四边形沿直线翻折,得到四边形FGDE,当点恰好落在线段上时,________.
275.矩形折叠求线段长(初二)
如图,在矩形中,,将向内翻折,点落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,则________.
276.矩形折叠三角函数求线段长(初三)
如图,在矩形中,为边上一点,将沿折叠,使得落到矩形内点的位置,连接,若,则________.
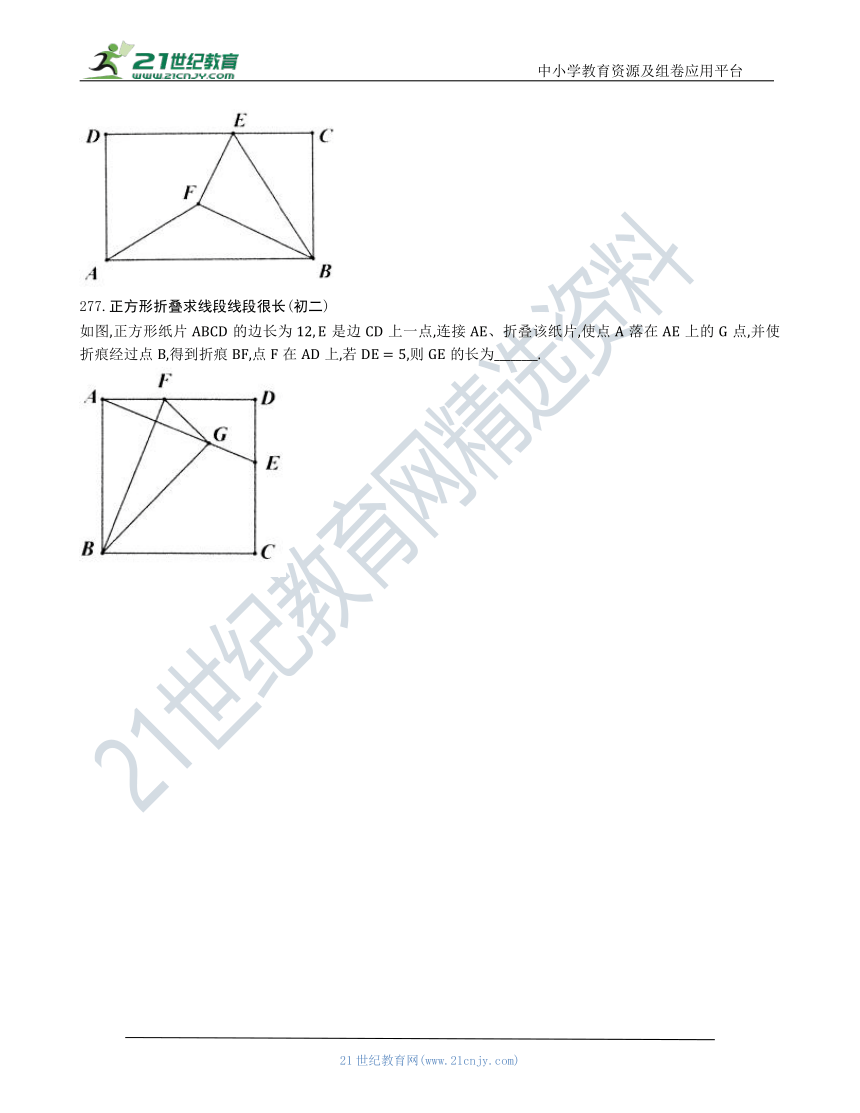
277.正方形折叠求线段线段很长(初二)
如图,正方形纸片的边长为是边上一点,连接折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上,若,则的长为________.
答案
268.【解】在中,,
.是斜边上的中线,
.
将沿对折,使点落在点处,
.故选:.
269.【解】,
由折叠可得,
又,
又中,-
,故选:.
270.【解】由折叠性质得:,由勾股定理的,则,在Rt中,设,则,解得:,同理:,由勾股定理构造方程,得.
故选:
271.【解】Rt中,,将边沿翻折,使点落在上的点处,,
,即,
,
在Rt中,,
将边沿翻折,使点落在延长线上的点
处,,
,
,且,
,
故选:.
272.【解】如图,过点作于.
,是等边二角形,
,
,
,
到直线的距离为,
故答案为.
273.【解】设,则,由翻折得:是以为腰的等腰三角形,分两种情况讨论:
(1)当时,矩形,
,由勾股定理得:,
解得:,
(2)当时,如图,作
,
沿翻折得
,
,
即,解得,综上所述:或.
故答案为:或.
274.【解】如图,过点作于,
将四边形沿直线翻折,得到四边形,
,
,
,
,故答案为:.
275.【解】由折叠可得,
,
,又,
,
Rt中,
,
故答案为:.
276.【解】过点作,交分别于点、,则,由折叠得:,
,设,则,在Rt中,由勾股定理得:
,解得:(舍去),,易证,即:,解得:.故答案为:.
277.【解】四边形为正方形,,,由折叠及轴对称的性质可知,垂直平分,,又,
,
,在Rt中,,
,
,
,故答案为:.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十三节:折叠模型
268.直角三角形折叠求角度(初二)
如图,在中,是斜边上的中线,将沿对折,使点落在点处,线段与相交于点,则等于( )
A.
B.
C.
D.
269.平行四边形折叠求角度(初二)
如图,将 沿对角线折叠,使点落在点处,交于点,若,则为( )
A.
B.
C.
D.
270.矩形折叠求线段(初二)
如图,矩形中,为对角线,将矩形沿所在直线折叠,使点落在上的点处,点落在上的点处,连接.已知,则的长为( )
A.3
B.5
C.
D.
271.直角三角形折叠求线段长(初二)
如图,在Rt中,,,将边沿翻折,使点落在上的点处,再将边沿翻折,使点落在延长线上的点处,两条折痕与斜边分别交于点,则线段的长为( )
A.
B.
C.
D.
272.三角形折叠求距离(初二)
如图,在中,,点在边上,,连接.如果将沿直线翻折后,点的对应点为点,那么点到直线的距离为________.
273.矩形折叠等腰三角形存在性讨论(初二)
如图,在矩形中,分别是边上一点,,将沿翻折得,连接,当________时,是以为腰的等腰三角形.
274.直接三角形折叠求线段的长(初二初三)
如图,在Rt中,,点在线段上,且,是线段上的一点,连接,将四边形沿直线翻折,得到四边形FGDE,当点恰好落在线段上时,________.
275.矩形折叠求线段长(初二)
如图,在矩形中,,将向内翻折,点落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,则________.
276.矩形折叠三角函数求线段长(初三)
如图,在矩形中,为边上一点,将沿折叠,使得落到矩形内点的位置,连接,若,则________.
277.正方形折叠求线段线段很长(初二)
如图,正方形纸片的边长为是边上一点,连接折叠该纸片,使点落在上的点,并使折痕经过点,得到折痕,点在上,若,则的长为________.
答案
268.【解】在中,,
.是斜边上的中线,
.
将沿对折,使点落在点处,
.故选:.
269.【解】,
由折叠可得,
又,
又中,-
,故选:.
270.【解】由折叠性质得:,由勾股定理的,则,在Rt中,设,则,解得:,同理:,由勾股定理构造方程,得.
故选:
271.【解】Rt中,,将边沿翻折,使点落在上的点处,,
,即,
,
在Rt中,,
将边沿翻折,使点落在延长线上的点
处,,
,
,且,
,
故选:.
272.【解】如图,过点作于.
,是等边二角形,
,
,
,
到直线的距离为,
故答案为.
273.【解】设,则,由翻折得:是以为腰的等腰三角形,分两种情况讨论:
(1)当时,矩形,
,由勾股定理得:,
解得:,
(2)当时,如图,作
,
沿翻折得
,
,
即,解得,综上所述:或.
故答案为:或.
274.【解】如图,过点作于,
将四边形沿直线翻折,得到四边形,
,
,
,
,故答案为:.
275.【解】由折叠可得,
,
,又,
,
Rt中,
,
故答案为:.
276.【解】过点作,交分别于点、,则,由折叠得:,
,设,则,在Rt中,由勾股定理得:
,解得:(舍去),,易证,即:,解得:.故答案为:.
277.【解】四边形为正方形,,,由折叠及轴对称的性质可知,垂直平分,,又,
,
,在Rt中,,
,
,
,故答案为:.
21世纪教育网(www.21cnjy.com)
同课章节目录
