【中考数学几何模型】第十三节:折叠模型258-267(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十三节:折叠模型258-267(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:03:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十三节:折叠模型
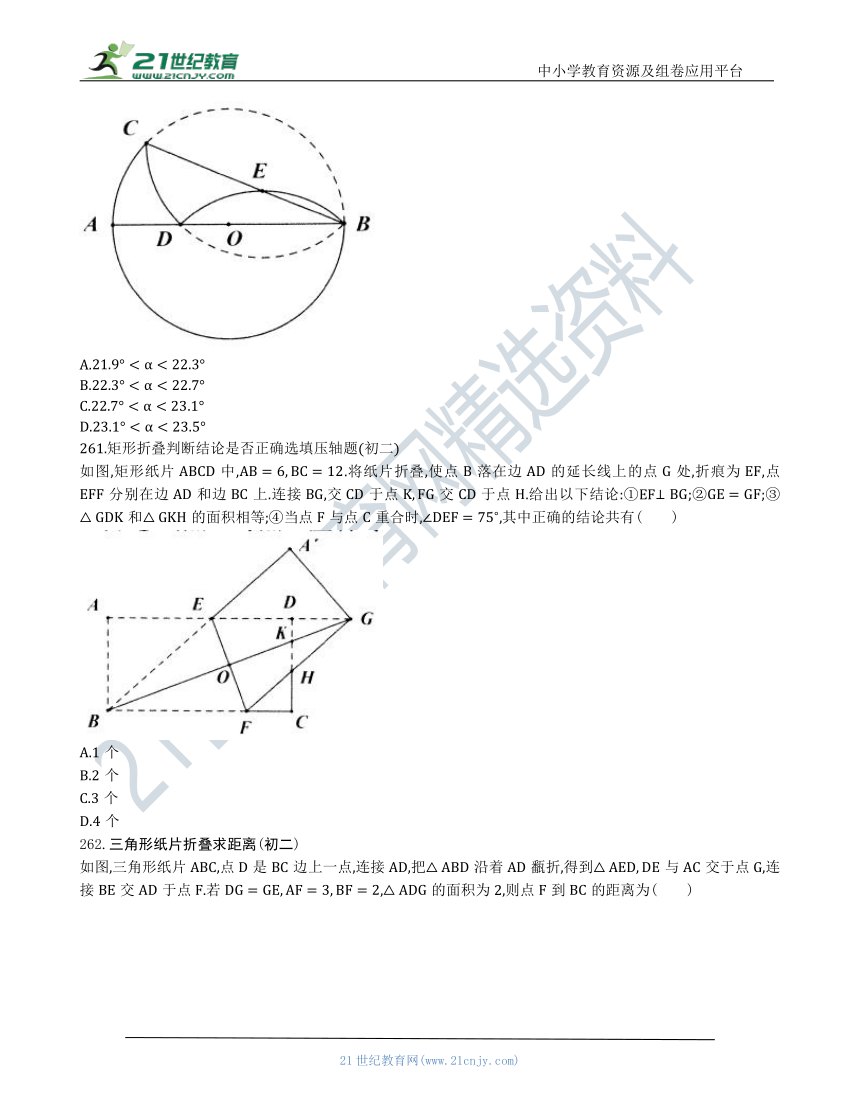
258.矩形两次翻折求线段长度折叠模型(初二)
如图,对折矩形纸片,使与重合,得到折痕,把纸片展平后再次折叠,使点落在上的点处,得到折痕与相交于点.若直线交直线于点,则的长为( )
A.
B.
C.
D.
259.矩形折叠求线段长度(初二)
如图,直线是矩形的对称轴,点在边上,将沿折叠,点恰好落在线段与的交点处,,则线段的长是( )
A.8
B.
C.
D.10
260.圆的翻折对应角相等对应弧相等
如图,是的直径,是的弦,先将弧沿翻折交于点,再将弧沿翻折交于点.若弧弧,设,则所在的范伟是( )
A.
B.
C.
D.
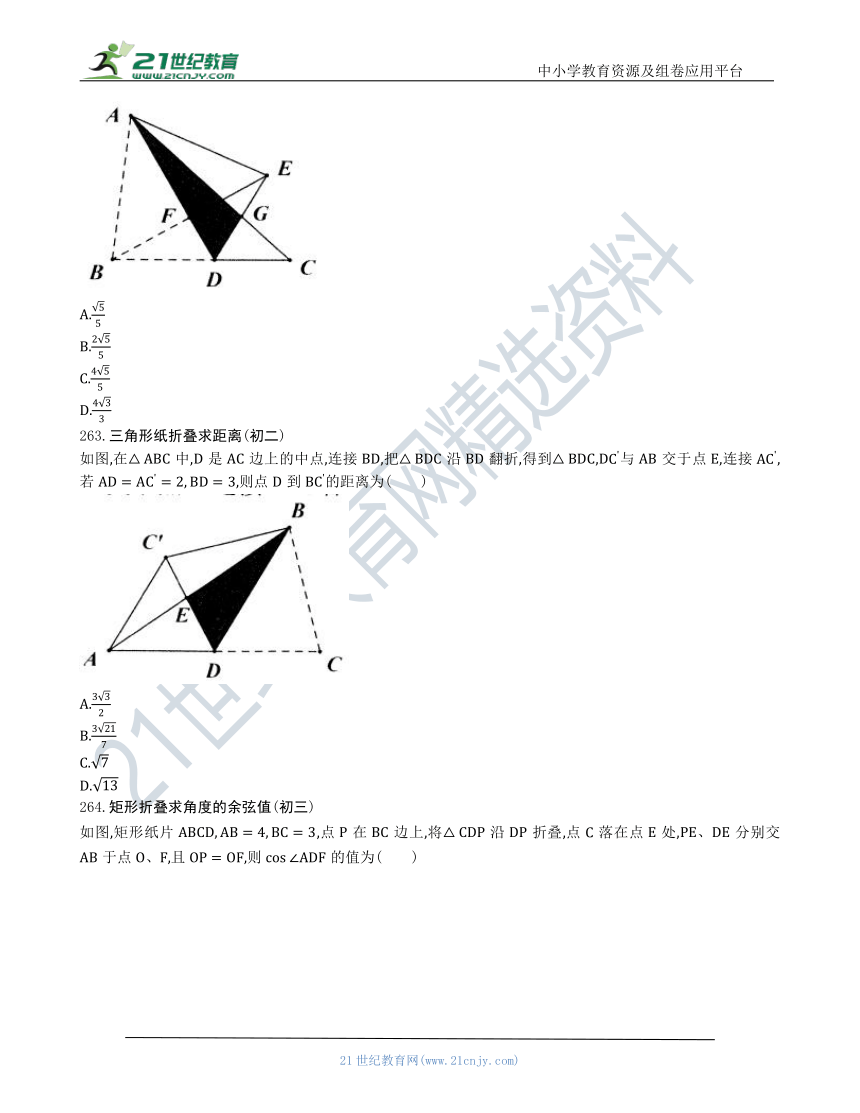
261.矩形折叠判断结论是否正确选填压轴题(初二)
如图,矩形纸片中,.将纸片折叠,使点落在边的延长线上的点处,折痕为,点分别在边和边上.连接,交于点交于点.给出以下结论:①EF;②;③和的面积相等;④当点与点重合时,,其中正确的结论共有( )
A.1个
B.2个
C.3个
D.4个
262.三角形纸片折叠求距离(初二)
如图,三角形纸片,点是边上一点,连接,把沿着 折,得到与交于点,连接交于点.若,的面积为2,则点到的距离为( )
A.
B.
C.
D.
263.三角形纸折叠求距离(初二)
如图,在中,是边上的中点,连接,把沿翻折,得到,与交于点,连接,若,则点到的距离为( )
A.
B.
C.
D.
264.矩形折叠求角度的余弦值(初三)
如图,矩形纸片,点在边上,将沿折叠,点C落在点处,分别交于点,且,则的值为( )
A.
B.
C.
D.
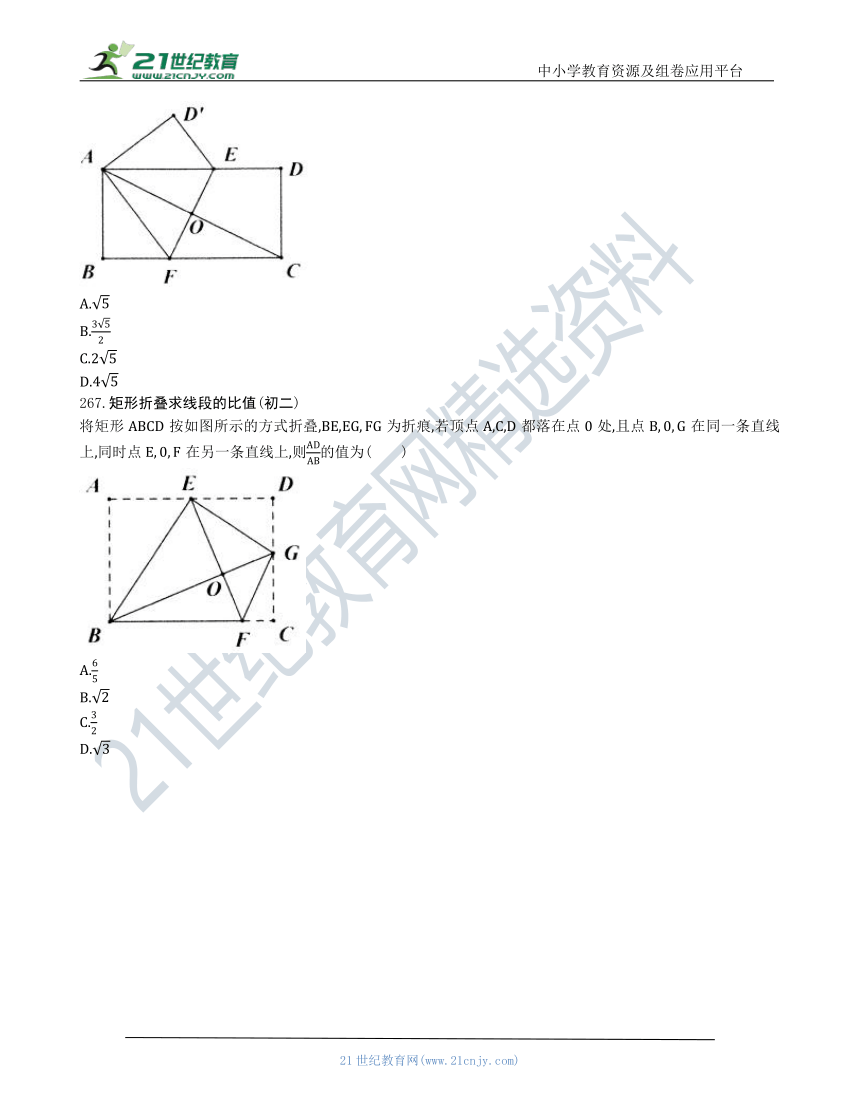
265.矩形折叠多结论判断正误选填压轴题题(初三)
如图所示,在矩形纸片中,,点分别是矩形的边、上的动点,将该纸片沿直线折叠.使点落在矩形边上,对应点记为点,点落在处,连接与交于点.则下列结论:①BN;②当点与点重合时,;③的面积的取值范围是;④当时,.其中成立的是( )
A.①③
B.③④
C.②③
D.②④
266.矩形折叠求线段长(初二)
如图,将矩形折叠,使点和点重合,折痕为与交于点0.若,则的长为( )
A.
B.
C.
D.
267.矩形折叠求线段的比值(初二)
将矩形按如图所示的方式折叠,BE,为折痕,若顶点A,C,D都落在点0处,且点在同一条直线上,同时点在另一条直线上,则的值为( )
A.
B.
C.
D.
答案
258.【解】连接由中位线定理得对折矩形纸片,使与重合,得到折痕把纸片展平后再次折叠,使点落在上的点处,得到折痕,
为等边三角形,
,
又,
,
.
在Rt中,,
,
.故选:.
259.【解】四边形是矩形,,由题意得:,由折叠的性质得:,
,
,在Rt中,,;故选:.
260.【解】如图,连接弧弧,,
弧弧弧,,
,
,
是直径,,,
故选:.
261.【解】如图,连接,设与交于点,
将纸片折叠,使点落在边的延长线上的点处,
垂直平分,
,故(1)正确,
,又,
,
,故(2)正确,
四边形是菱形,
,当点与点重合时,则,
,
,故(4)正确,
平分,只有当时,,而此时,故(3)错误;故选:.
262.【解】,
由翻折可知,,
,
,
,
设点到的距离为,则有,
,故选:.
263.【解】如图,连接,交于点,过点作于点是边上的中点,,由翻折知,,
垂直平分,
为等边三角形,
,
,
在Rt中,,
在Rt中,,
,
,故选:.
264.【解】根据折叠,可知:,
.
在和中,,
.
设,则,
又.在Rt中,,
即,解得:,
.故选:.
265.【解】是定值,的长是变化的,的值也是变化的,与不一定相等,故(1)错误.
四边形是矩形,,
由翻折的性质可知,
,
四边形是平行四边形,,
四边形是菱形,,
如图,当重合时,设,在Rt
中,则有,
,
,
,故(2)正确,
266.【解】矩形,
,由折叠得,,
,
由折叠得,,
在Rt中,,
在Rt中,,
,故选:.
267.【解】由折叠可得,,
分别为的中点,设,
则
中,,
即,即,
的值为,故选:.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十三节:折叠模型
258.矩形两次翻折求线段长度折叠模型(初二)
如图,对折矩形纸片,使与重合,得到折痕,把纸片展平后再次折叠,使点落在上的点处,得到折痕与相交于点.若直线交直线于点,则的长为( )
A.
B.
C.
D.
259.矩形折叠求线段长度(初二)
如图,直线是矩形的对称轴,点在边上,将沿折叠,点恰好落在线段与的交点处,,则线段的长是( )
A.8
B.
C.
D.10
260.圆的翻折对应角相等对应弧相等
如图,是的直径,是的弦,先将弧沿翻折交于点,再将弧沿翻折交于点.若弧弧,设,则所在的范伟是( )
A.
B.
C.
D.
261.矩形折叠判断结论是否正确选填压轴题(初二)
如图,矩形纸片中,.将纸片折叠,使点落在边的延长线上的点处,折痕为,点分别在边和边上.连接,交于点交于点.给出以下结论:①EF;②;③和的面积相等;④当点与点重合时,,其中正确的结论共有( )
A.1个
B.2个
C.3个
D.4个
262.三角形纸片折叠求距离(初二)
如图,三角形纸片,点是边上一点,连接,把沿着 折,得到与交于点,连接交于点.若,的面积为2,则点到的距离为( )
A.
B.
C.
D.
263.三角形纸折叠求距离(初二)
如图,在中,是边上的中点,连接,把沿翻折,得到,与交于点,连接,若,则点到的距离为( )
A.
B.
C.
D.
264.矩形折叠求角度的余弦值(初三)
如图,矩形纸片,点在边上,将沿折叠,点C落在点处,分别交于点,且,则的值为( )
A.
B.
C.
D.
265.矩形折叠多结论判断正误选填压轴题题(初三)
如图所示,在矩形纸片中,,点分别是矩形的边、上的动点,将该纸片沿直线折叠.使点落在矩形边上,对应点记为点,点落在处,连接与交于点.则下列结论:①BN;②当点与点重合时,;③的面积的取值范围是;④当时,.其中成立的是( )
A.①③
B.③④
C.②③
D.②④
266.矩形折叠求线段长(初二)
如图,将矩形折叠,使点和点重合,折痕为与交于点0.若,则的长为( )
A.
B.
C.
D.
267.矩形折叠求线段的比值(初二)
将矩形按如图所示的方式折叠,BE,为折痕,若顶点A,C,D都落在点0处,且点在同一条直线上,同时点在另一条直线上,则的值为( )
A.
B.
C.
D.
答案
258.【解】连接由中位线定理得对折矩形纸片,使与重合,得到折痕把纸片展平后再次折叠,使点落在上的点处,得到折痕,
为等边三角形,
,
又,
,
.
在Rt中,,
,
.故选:.
259.【解】四边形是矩形,,由题意得:,由折叠的性质得:,
,
,在Rt中,,;故选:.
260.【解】如图,连接弧弧,,
弧弧弧,,
,
,
是直径,,,
故选:.
261.【解】如图,连接,设与交于点,
将纸片折叠,使点落在边的延长线上的点处,
垂直平分,
,故(1)正确,
,又,
,
,故(2)正确,
四边形是菱形,
,当点与点重合时,则,
,
,故(4)正确,
平分,只有当时,,而此时,故(3)错误;故选:.
262.【解】,
由翻折可知,,
,
,
,
设点到的距离为,则有,
,故选:.
263.【解】如图,连接,交于点,过点作于点是边上的中点,,由翻折知,,
垂直平分,
为等边三角形,
,
,
在Rt中,,
在Rt中,,
,
,故选:.
264.【解】根据折叠,可知:,
.
在和中,,
.
设,则,
又.在Rt中,,
即,解得:,
.故选:.
265.【解】是定值,的长是变化的,的值也是变化的,与不一定相等,故(1)错误.
四边形是矩形,,
由翻折的性质可知,
,
四边形是平行四边形,,
四边形是菱形,,
如图,当重合时,设,在Rt
中,则有,
,
,
,故(2)正确,
266.【解】矩形,
,由折叠得,,
,
由折叠得,,
在Rt中,,
在Rt中,,
,故选:.
267.【解】由折叠可得,,
分别为的中点,设,
则
中,,
即,即,
的值为,故选:.
21世纪教育网(www.21cnjy.com)
同课章节目录
