【中考数学几何模型】第十五节:对角互补模型298-306(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十五节:对角互补模型298-306(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:05:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十五节:对角互补模型
298.对角互补旋转模型判断结论对错(初二)
如图,为等边三角形,以为边向形外作,使,再以点为旋转中心把旋转到,则下列结论:①D、A、三点共线;②平分;③;④.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
299.对角互补四点共圆模型多结论判断题(初三)
如图,正方形,点是对角线上一点,连接,过作交于,连接交于,若为中点,则下列结论:
①;②;③;④正方形的面积是16;
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
300.等腰三角形中的对角互补模型(初二)
已知中,,点为边的中点,、分别交于点.
(1)如图1,若.求证:.
(2)如图2,若与不平行.则问题(1)的结论是否成立 说明理由.
301.对角互补模型新定义理解探究运用(初三)
定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:(1)如图1,点在上,的平分线交于点,连接.求证:四边形是等补四边形;
探究:(2)如图2,在等补四边形中,,连接是否平分 请说明理由.
运用:(3)如图3,在等补四边形中,,其外角的平分线交的延长线于点,求的长.
302.坐标系中旋转型对角互补模型(初二)
如图,点在第一象限的角平分线上,,点在轴正半轴上,点在轴正半轴上.
(1)求点的坐标.
(2)当绕点旋转时,
①的值是否发生变化 若变化,求出其变化范围;若不变,求出这个定值.
②请求出的最小值.
303.对角互补模型求面积最大值(初三)
(1)如图①,等边的边长为6,则该等边三角形的外接圆半径长为________.
(2)如图②,在中,,点分别在边、和上,,若点为边的中点,,求的长度.
(3)如图(3),在中,,等边的三个顶点分别在边上.该等边三角形的面积是否存在最大值,如果存在,求出面积最大值,如果不存在,说明理由.
304.对角互补模型新定义探究应用(初三)
定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有________.
(2)性质探究:
①如图1,四边形是奇异四边形,,求证:平分;
②如图2,四边形是奇异四边形,,试说明:
(3)性质应用:
如图3,四边形是奇异四边形,四条边中仅有,且四边形的周长为,求奇异四边形的面积.
305.对角互补模型新定义探究(初三)
定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形中,与是一组对角,若,则________°.
②如图1,在中,点分别在边上,且,求证:四边形ADEC是互补四边形.
(2)探究发现:如图2,在等腰中,,点分别在边上,,四边形是互补四边形,求证:.
306.梯子模型的结论和解题技巧(初三)
如图,在平面直角坐标系中,矩形的边.若不改变矩形的形状和大小,当矩形顶点在轴的正半轴上左右移动时,矩形的另一个顶点始终在轴的正半轴上随之上下移动.
(1)当时,求点的坐标;
(2)设的中点为,连接,当四边形的面积为时,求的长;
(3)当点移动到某一位置时,点到点的距离有最大值,请直接写出最大值,并求此时的值.
答案
298.【解】如图,①设度,则,故、、三点共线;故①正确;
②绕着点按顺时针方向旋转得到为等边三角形,DC平分∠BDA;故②正确;
③故③正确;
④由旋转可知AE=BD.又
ΔCDE为等边三角形,∴DC=DB+BA.故④正确;故选:A.
299.【解】四边形是正方形,.
、、、四点共圆,①正确;③正确;
四边形是正方形,②正确.
过作于于,则、、三点共线.
四边形是正方形,是等腰直角三角形,.
在和中,易证(ASA),.
为中点,正方形的面积是④正确;故选:.
300.【解】(1)∥.又.又是中点,.
(2)如图,连接是等腰三角形,点为边的中点,.
在线段上取点,使,连接,
在与中,.
在四边形中,
.
.
方法2(初三):四点共圆.(三线合一),.
301.【解】(1)证明:四边形为圆内接四边形,.
平分四边形是等补四边形;
(2)平分,理由如下:
如图2,过点分别作于点垂直的延长线于点,则.
四边形是等补四边形,,
又.
是的平分线,即平分;
(3)如图3,连接四边形是等补四边形,,又
平分,,由(2)知,平分
又.
即.
302.【解】(1)点在第一象限的角平分线上,;
(2)①不变.过点作轴于于
,四边形是正方形,.
在和中,
②连接.
,当最小时,也最小.根据垂线段最短原理,最小值为2,的最小值为8.
303.【解】(1)如图1,作、的垂直平分线,交的内部于一点即为等边三角形的外接圆的圆心,则,
在Rt中,等边三角形的外接圆半径长为.
(2)如图2,连接,过点作于点于点,则.
,点是的中点,
在和中,
在四边形AMDN中,
即
在和中,
在Rt中,,
在Rt中,
(3)如图3,过点作于点于点,由(2)可得:.
,且由几何关系可得取得最大值时,取得最大值,作的外接圆,连接、,则.
.
过点作交于、,垂足为,则平分弧,弧弧,连接、、共线.
由几何关系可得:.
当最小时,存在最大值,当为直径时,存在最大值,最大.
304.【解】(1)根据奇异四边形的定义可知:正方形是奇异四边形,故答案为正方形.
(2)①如图1,过点作于于.
.
.
AM⊥CB于M,AN⊥CD于N,∴CA平分∠BCD.
②由①可知:
.在Rt中,.
(3)如图3中,由(2)可知:
四边形的周长为
四边形是奇异四边形,
.
.
305.(1)①【解】四边形是互补四边形,与是一组对角,.
.
,故答案为:90;
②证明:.又
四边形是互补四边形;
(2)证明:.
在和中,.
.
四边形是互补四边形,.
.
306.【解】(1)如图1,过点作轴于点矩形中,.
又在Rt中,.
在Rt中,点的坐标为;
(2)为的中点,,
又.
设、,则,即,将代入得,解得(负值舍去),;
(3)的最大值为8,如图为的中点,
当、、三点在同一直线时,有最大值8,连接,则此时与的交点为.过点作,垂足为
即,解得
.
在Rt中,
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十五节:对角互补模型
298.对角互补旋转模型判断结论对错(初二)
如图,为等边三角形,以为边向形外作,使,再以点为旋转中心把旋转到,则下列结论:①D、A、三点共线;②平分;③;④.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
299.对角互补四点共圆模型多结论判断题(初三)
如图,正方形,点是对角线上一点,连接,过作交于,连接交于,若为中点,则下列结论:
①;②;③;④正方形的面积是16;
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
300.等腰三角形中的对角互补模型(初二)
已知中,,点为边的中点,、分别交于点.
(1)如图1,若.求证:.
(2)如图2,若与不平行.则问题(1)的结论是否成立 说明理由.
301.对角互补模型新定义理解探究运用(初三)
定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:(1)如图1,点在上,的平分线交于点,连接.求证:四边形是等补四边形;
探究:(2)如图2,在等补四边形中,,连接是否平分 请说明理由.
运用:(3)如图3,在等补四边形中,,其外角的平分线交的延长线于点,求的长.
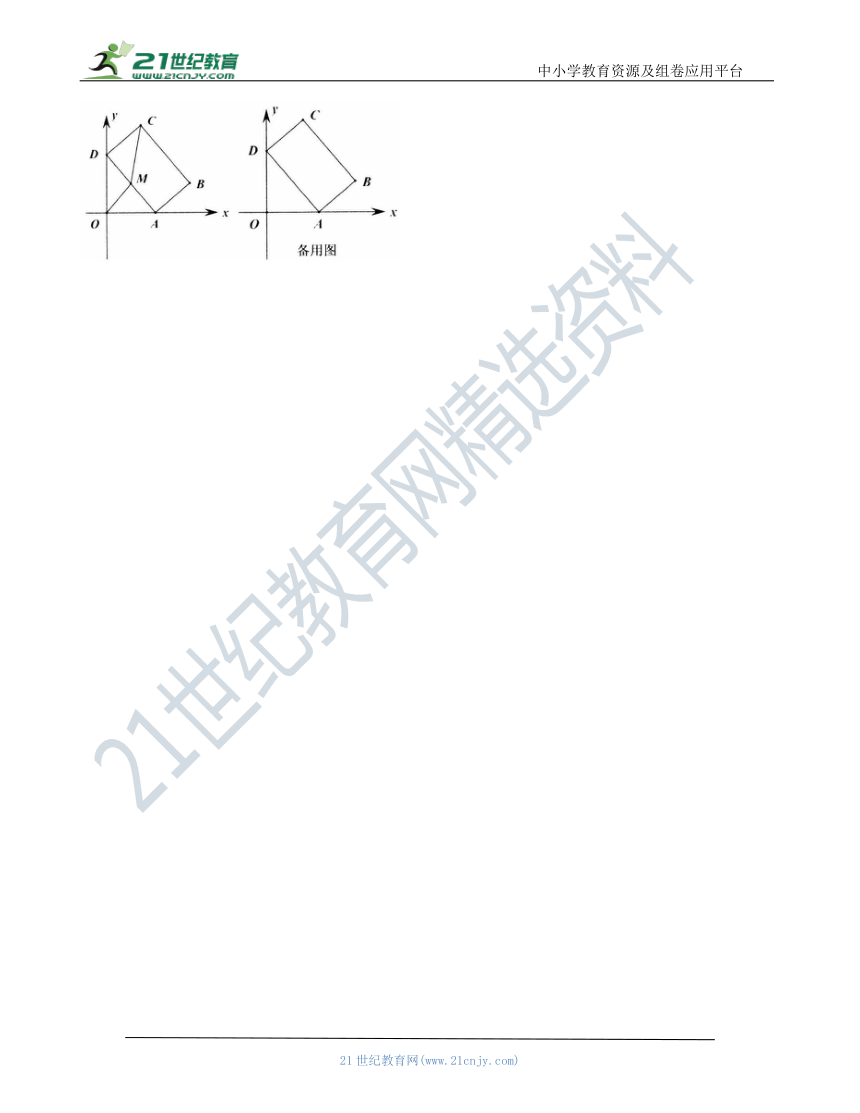
302.坐标系中旋转型对角互补模型(初二)
如图,点在第一象限的角平分线上,,点在轴正半轴上,点在轴正半轴上.
(1)求点的坐标.
(2)当绕点旋转时,
①的值是否发生变化 若变化,求出其变化范围;若不变,求出这个定值.
②请求出的最小值.
303.对角互补模型求面积最大值(初三)
(1)如图①,等边的边长为6,则该等边三角形的外接圆半径长为________.
(2)如图②,在中,,点分别在边、和上,,若点为边的中点,,求的长度.
(3)如图(3),在中,,等边的三个顶点分别在边上.该等边三角形的面积是否存在最大值,如果存在,求出面积最大值,如果不存在,说明理由.
304.对角互补模型新定义探究应用(初三)
定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有________.
(2)性质探究:
①如图1,四边形是奇异四边形,,求证:平分;
②如图2,四边形是奇异四边形,,试说明:
(3)性质应用:
如图3,四边形是奇异四边形,四条边中仅有,且四边形的周长为,求奇异四边形的面积.
305.对角互补模型新定义探究(初三)
定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形中,与是一组对角,若,则________°.
②如图1,在中,点分别在边上,且,求证:四边形ADEC是互补四边形.
(2)探究发现:如图2,在等腰中,,点分别在边上,,四边形是互补四边形,求证:.
306.梯子模型的结论和解题技巧(初三)
如图,在平面直角坐标系中,矩形的边.若不改变矩形的形状和大小,当矩形顶点在轴的正半轴上左右移动时,矩形的另一个顶点始终在轴的正半轴上随之上下移动.
(1)当时,求点的坐标;
(2)设的中点为,连接,当四边形的面积为时,求的长;
(3)当点移动到某一位置时,点到点的距离有最大值,请直接写出最大值,并求此时的值.
答案
298.【解】如图,①设度,则,故、、三点共线;故①正确;
②绕着点按顺时针方向旋转得到为等边三角形,DC平分∠BDA;故②正确;
③故③正确;
④由旋转可知AE=BD.又
ΔCDE为等边三角形,∴DC=DB+BA.故④正确;故选:A.
299.【解】四边形是正方形,.
、、、四点共圆,①正确;③正确;
四边形是正方形,②正确.
过作于于,则、、三点共线.
四边形是正方形,是等腰直角三角形,.
在和中,易证(ASA),.
为中点,正方形的面积是④正确;故选:.
300.【解】(1)∥.又.又是中点,.
(2)如图,连接是等腰三角形,点为边的中点,.
在线段上取点,使,连接,
在与中,.
在四边形中,
.
.
方法2(初三):四点共圆.(三线合一),.
301.【解】(1)证明:四边形为圆内接四边形,.
平分四边形是等补四边形;
(2)平分,理由如下:
如图2,过点分别作于点垂直的延长线于点,则.
四边形是等补四边形,,
又.
是的平分线,即平分;
(3)如图3,连接四边形是等补四边形,,又
平分,,由(2)知,平分
又.
即.
302.【解】(1)点在第一象限的角平分线上,;
(2)①不变.过点作轴于于
,四边形是正方形,.
在和中,
②连接.
,当最小时,也最小.根据垂线段最短原理,最小值为2,的最小值为8.
303.【解】(1)如图1,作、的垂直平分线,交的内部于一点即为等边三角形的外接圆的圆心,则,
在Rt中,等边三角形的外接圆半径长为.
(2)如图2,连接,过点作于点于点,则.
,点是的中点,
在和中,
在四边形AMDN中,
即
在和中,
在Rt中,,
在Rt中,
(3)如图3,过点作于点于点,由(2)可得:.
,且由几何关系可得取得最大值时,取得最大值,作的外接圆,连接、,则.
.
过点作交于、,垂足为,则平分弧,弧弧,连接、、共线.
由几何关系可得:.
当最小时,存在最大值,当为直径时,存在最大值,最大.
304.【解】(1)根据奇异四边形的定义可知:正方形是奇异四边形,故答案为正方形.
(2)①如图1,过点作于于.
.
.
AM⊥CB于M,AN⊥CD于N,∴CA平分∠BCD.
②由①可知:
.在Rt中,.
(3)如图3中,由(2)可知:
四边形的周长为
四边形是奇异四边形,
.
.
305.(1)①【解】四边形是互补四边形,与是一组对角,.
.
,故答案为:90;
②证明:.又
四边形是互补四边形;
(2)证明:.
在和中,.
.
四边形是互补四边形,.
.
306.【解】(1)如图1,过点作轴于点矩形中,.
又在Rt中,.
在Rt中,点的坐标为;
(2)为的中点,,
又.
设、,则,即,将代入得,解得(负值舍去),;
(3)的最大值为8,如图为的中点,
当、、三点在同一直线时,有最大值8,连接,则此时与的交点为.过点作,垂足为
即,解得
.
在Rt中,
21世纪教育网(www.21cnjy.com)
同课章节目录
