【中考数学几何模型】第十一节:中点模型223-232(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十一节:中点模型223-232(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:06:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十一节:中点模型
223.利用三角形中位线定理求线段的长中点模型(初二)
如图,已知点在正方形的边上,以为边向正方形外部作正方形,连接分别是的中点,连接.若,则________.
224.构造三角形中位线中点模型求线段的长(初二)
如图,在中,是边的中点,是边上一点.若平分的周长,则的长是________.
225.中点模型倍长类中线有全等巧用勾股定理(初二)
如图,在Rt中,点为的中点,交于,交于,若,则的长是_________.
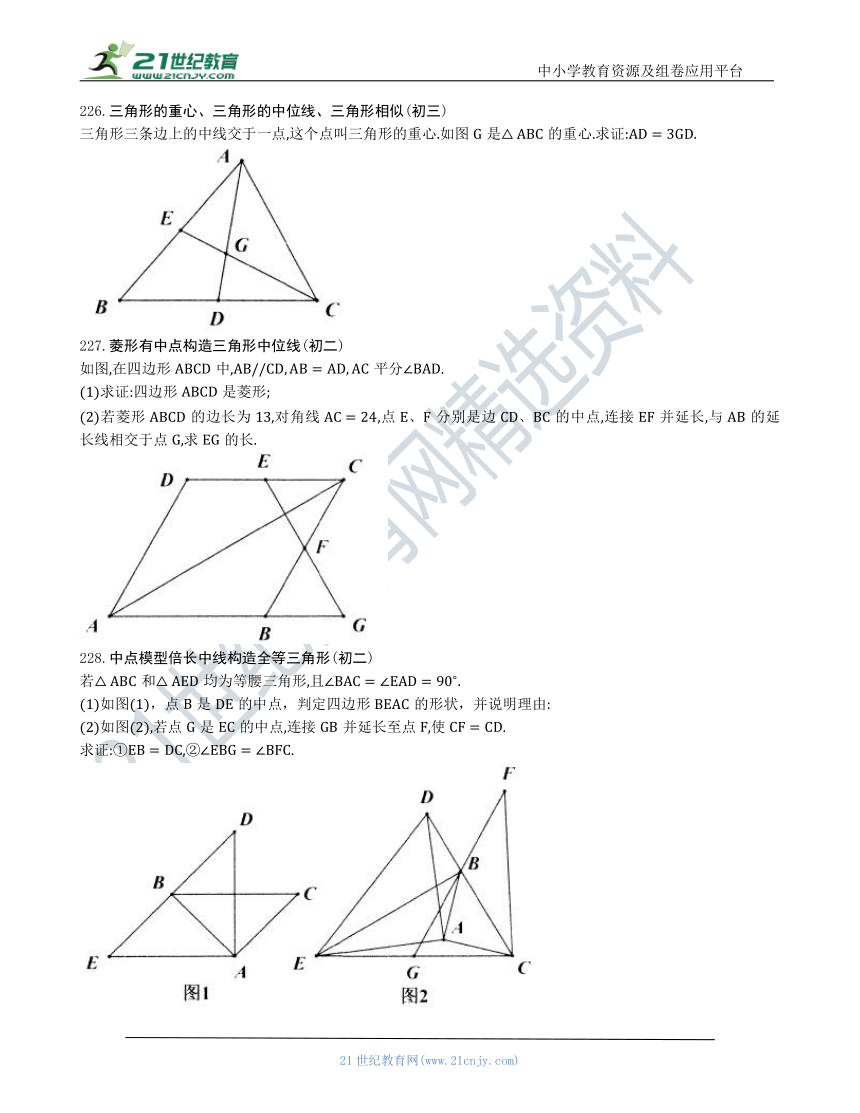
226.三角形的重心、三角形的中位线、三角形相似(初三)
三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
227.菱形有中点构造三角形中位线(初二)
如图,在四边形中,平分.
(1)求证:四边形是菱形;
(2)若菱形的边长为13,对角线,点分别是边的中点,连接并延长,与的延长线相交于点,求的长.
228.中点模型倍长中线构造全等三角形(初二)
若和均为等腰三角形,且.
(1)如图(1),点是DE的中点,判定四边形BEAC的形状,并说明理由:
(2)如图(2),若点是的中点,连接并延长至点,使.
求证:①,②.
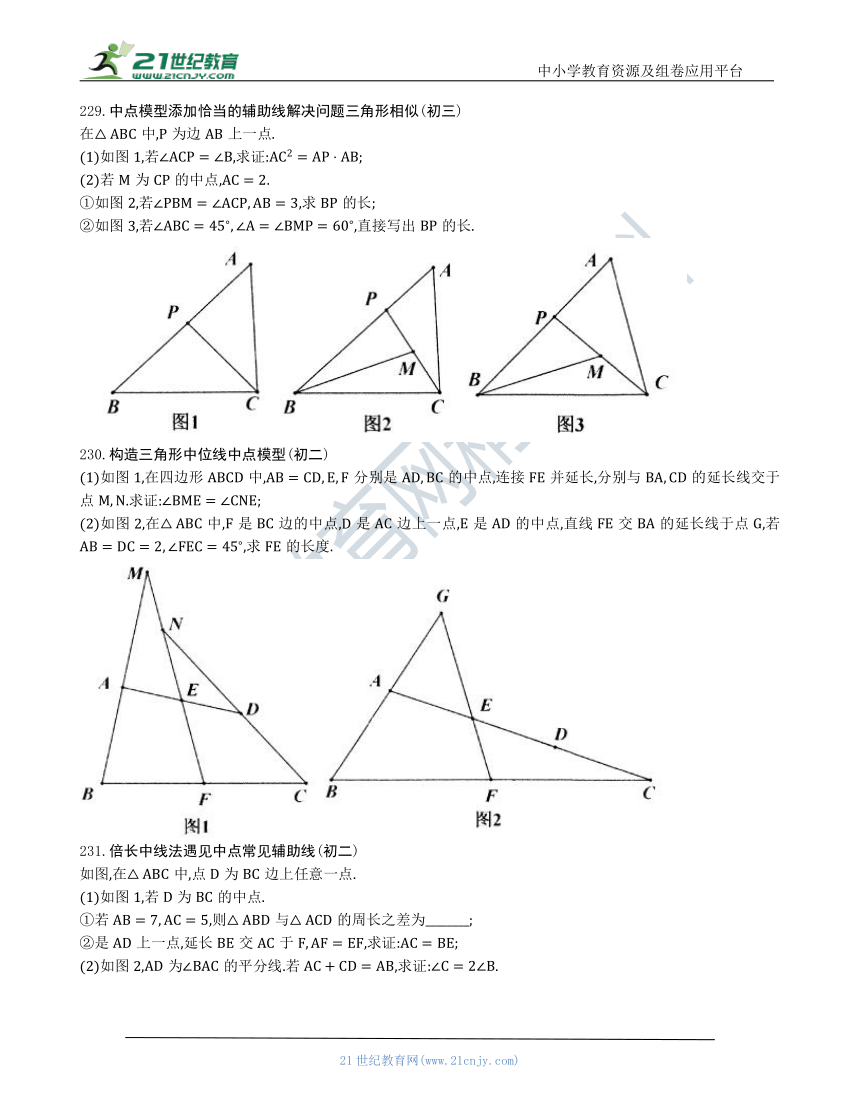
229.中点模型添加恰当的辅助线解决问题三角形相似(初三)
在中,为边上一点.
(1)如图1,若,求证:;
(2)若为的中点,.
①如图2,若,求的长;
②如图3,若,直接写出的长.
230.构造三角形中位线中点模型(初二)
(1)如图1,在四边形中,分别是的中点,连接并延长,分别与的延长线交于点.求证:;
(2)如图2,在中,是边的中点,D是边上一点,是的中点,直线交的延长线于点,若,求的长度.
231.倍长中线法遇见中点常见辅助线(初二)
如图,在中,点为边上任意一点.
(1)如图1,若为的中点.
①若,则与的周长之差为________;
②是上一点,延长交于,求证:;
(2)如图2,为的平分线.若,求证:.
232.遇见中点中线辅助线添加方法(初二)
【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①,中,若,,求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长至点,使,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到,依据是________.
A.SAS
B.SSS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得的取值范围是________.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】如图②,是的中线,交于,交于,且,若,求线段的长.
【灵活运用】如图③,在中,为中点,交于点交于点,连接,试猜想线段三者之间的数量关系,并证明你的结论。
答案
223.【解】连接,
正方形和正方形中,,
,
.分别是的中点,.故答案为:.
224.【解】延长至,使,连接,作于平分的周长,,又是的中位线,,,
,,故答案为:.
225.【解】如图,过点作交的延长线于点,连接点是的中点,,
,
在和中,
,
.在Rt中,2,故答案为:2.
226.证明:连接,
点是的重心,点和点分别是和的中点,是的中位线,且,,即.
227.【解】(1)平分,
,
,又,
且四边形是平行四边形,
四边形是菱形.
(2)连接,交于点,(自行画图)
菱形的边长为13,对角线,
点分别是边的中点,
(中位线),是菱形的对角线,
,又,
四边形是平行四边形,
.在中.,
..
228.【解】(1)四边形是平行四边形,理由如下:为等腰三角形,是的中点,,
是等腰三角形,,
,
四边形是平行四边形;
(2)(1)和均为等腰直角三角形,
,
,
(2)延长至点,使,是的中点,,
又,
,
,
,
.
229.【解】(1),
;
图1图2
(2)如图2,连接,取的中点,连接,分别是的中点,是的中位(2).(1)如图2,取的中点,连接,设,则是的中点,,
,即,线,是的中位线,,是等腰直角二角形,.
,
;
图2图3
(2)如图3,过作于,延长到,使,设.,,
,
,
,
,
,
,
,
.
230.(1)证明:如图1,连接,取的中点,连接分别是的中点.
是的中位线,
分别是的中点,
是的中位线,
,
;
231.【解】(1)为的中点,,
与的周长之差为,.故答案为:2.
(2)证明:如图1,延长至,使,连接,是的中点,,
在和中,,
,
;
图1图2
(2)证明:如图2,在上截取,连接,
是的平分线,,
在和中,
,
,且,
,,
即.
232.【问题情境】【解】(1)在和中,
故选:;
(2)由(1)得:,
在中,,即,故答案为:;
【初步运用】【解】延长到,使,连接,如图(2)所示:是中线,,
在和中,,
,
,
;
【灵活运用】【解】线段之间的等量关系为:.理由如下:延长到点,使,连接,如图(3)所示:
是的中点,
,在和中,
,
,
,
即,Rt中,由勾股定理得:
.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十一节:中点模型
223.利用三角形中位线定理求线段的长中点模型(初二)
如图,已知点在正方形的边上,以为边向正方形外部作正方形,连接分别是的中点,连接.若,则________.
224.构造三角形中位线中点模型求线段的长(初二)
如图,在中,是边的中点,是边上一点.若平分的周长,则的长是________.
225.中点模型倍长类中线有全等巧用勾股定理(初二)
如图,在Rt中,点为的中点,交于,交于,若,则的长是_________.
226.三角形的重心、三角形的中位线、三角形相似(初三)
三角形三条边上的中线交于一点,这个点叫三角形的重心.如图是的重心.求证:.
227.菱形有中点构造三角形中位线(初二)
如图,在四边形中,平分.
(1)求证:四边形是菱形;
(2)若菱形的边长为13,对角线,点分别是边的中点,连接并延长,与的延长线相交于点,求的长.
228.中点模型倍长中线构造全等三角形(初二)
若和均为等腰三角形,且.
(1)如图(1),点是DE的中点,判定四边形BEAC的形状,并说明理由:
(2)如图(2),若点是的中点,连接并延长至点,使.
求证:①,②.
229.中点模型添加恰当的辅助线解决问题三角形相似(初三)
在中,为边上一点.
(1)如图1,若,求证:;
(2)若为的中点,.
①如图2,若,求的长;
②如图3,若,直接写出的长.
230.构造三角形中位线中点模型(初二)
(1)如图1,在四边形中,分别是的中点,连接并延长,分别与的延长线交于点.求证:;
(2)如图2,在中,是边的中点,D是边上一点,是的中点,直线交的延长线于点,若,求的长度.
231.倍长中线法遇见中点常见辅助线(初二)
如图,在中,点为边上任意一点.
(1)如图1,若为的中点.
①若,则与的周长之差为________;
②是上一点,延长交于,求证:;
(2)如图2,为的平分线.若,求证:.
232.遇见中点中线辅助线添加方法(初二)
【问题情境】课外兴趣小组活动时,老师提出了如下问题:
如图①,中,若,,求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长至点,使,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到,依据是________.
A.SAS
B.SSS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得的取值范围是________.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】如图②,是的中线,交于,交于,且,若,求线段的长.
【灵活运用】如图③,在中,为中点,交于点交于点,连接,试猜想线段三者之间的数量关系,并证明你的结论。
答案
223.【解】连接,
正方形和正方形中,,
,
.分别是的中点,.故答案为:.
224.【解】延长至,使,连接,作于平分的周长,,又是的中位线,,,
,,故答案为:.
225.【解】如图,过点作交的延长线于点,连接点是的中点,,
,
在和中,
,
.在Rt中,2,故答案为:2.
226.证明:连接,
点是的重心,点和点分别是和的中点,是的中位线,且,,即.
227.【解】(1)平分,
,
,又,
且四边形是平行四边形,
四边形是菱形.
(2)连接,交于点,(自行画图)
菱形的边长为13,对角线,
点分别是边的中点,
(中位线),是菱形的对角线,
,又,
四边形是平行四边形,
.在中.,
..
228.【解】(1)四边形是平行四边形,理由如下:为等腰三角形,是的中点,,
是等腰三角形,,
,
四边形是平行四边形;
(2)(1)和均为等腰直角三角形,
,
,
(2)延长至点,使,是的中点,,
又,
,
,
,
.
229.【解】(1),
;
图1图2
(2)如图2,连接,取的中点,连接,分别是的中点,是的中位(2).(1)如图2,取的中点,连接,设,则是的中点,,
,即,线,是的中位线,,是等腰直角二角形,.
,
;
图2图3
(2)如图3,过作于,延长到,使,设.,,
,
,
,
,
,
,
,
.
230.(1)证明:如图1,连接,取的中点,连接分别是的中点.
是的中位线,
分别是的中点,
是的中位线,
,
;
231.【解】(1)为的中点,,
与的周长之差为,.故答案为:2.
(2)证明:如图1,延长至,使,连接,是的中点,,
在和中,,
,
;
图1图2
(2)证明:如图2,在上截取,连接,
是的平分线,,
在和中,
,
,且,
,,
即.
232.【问题情境】【解】(1)在和中,
故选:;
(2)由(1)得:,
在中,,即,故答案为:;
【初步运用】【解】延长到,使,连接,如图(2)所示:是中线,,
在和中,,
,
,
;
【灵活运用】【解】线段之间的等量关系为:.理由如下:延长到点,使,连接,如图(3)所示:
是的中点,
,在和中,
,
,
,
即,Rt中,由勾股定理得:
.
21世纪教育网(www.21cnjy.com)
同课章节目录
