【中考数学几何模型】第十二节:旋转模型233-240(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十二节:旋转模型233-240(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:07:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十二节:旋转模型
233.线段旋转变换后,勾股定理求三角形面积(初二)
如图,为等边三角形内的一点,且到三个顶点的距离分别为3,4,5,则的面积为( )
A.
B.
C.
D.
234.旋转模型手拉手全等求最大值(初二)
如图,平面内三点,以为对角线作正方形,连接,则的最大值是( )
A.
B.
C.4
D.8
235.线段旋转过程中隐形圆求它的最大值
如图,在矩形中,点是的中点,点是的中点,连接是的中点,连接.在中,,若将绕点逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A.
B.
C.10
D.12
236.旋转变换后勾股定理求正方形面积(初二)
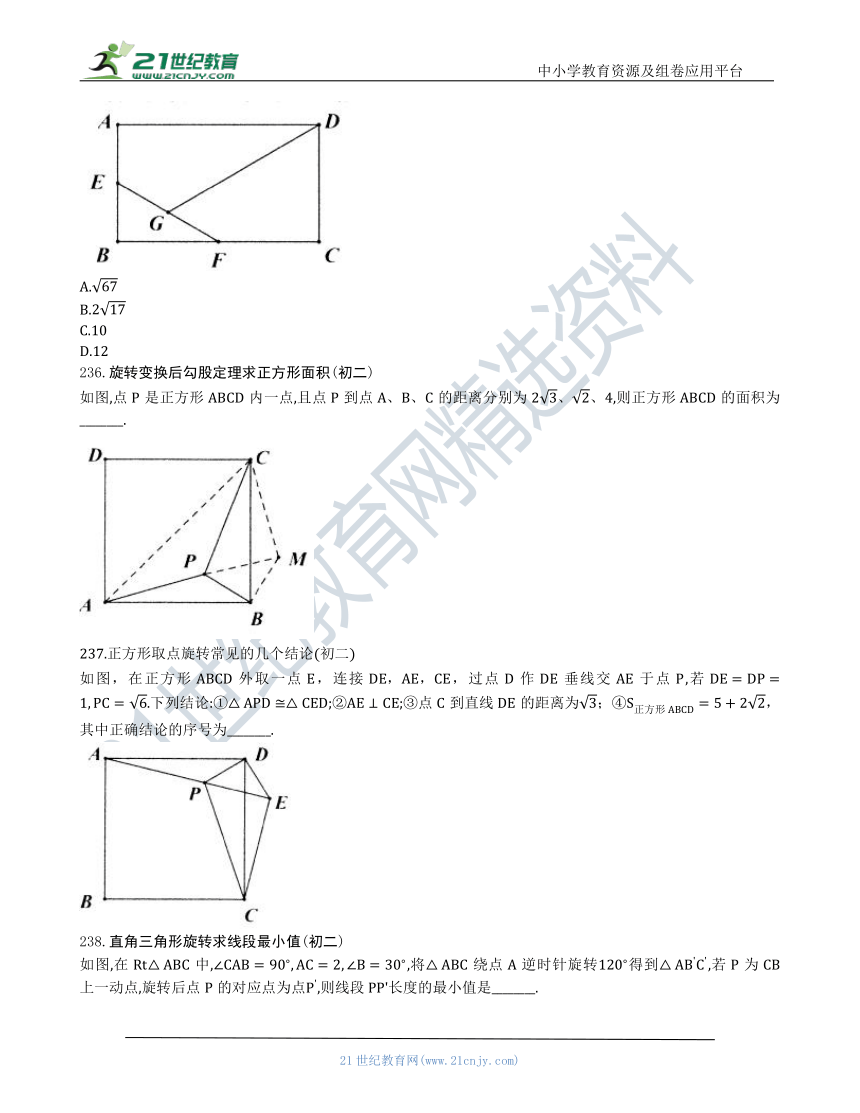
如图,点是正方形内一点,且点到点的距离分别为、4,则正方形的面积为________.
237.正方形取点旋转常见的几个结论(初二)
如图,在正方形外取一点,连接,过点作垂线交于点,若.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为________.
238.直角三角形旋转求线段最小值(初二)
如图,在Rt中,,将绕点逆时针旋转得到,若为上一动点,旋转后点的对应点为点,则线段PP'长度的最小值是________.
239.正方形旋转求线段最小值(初二)
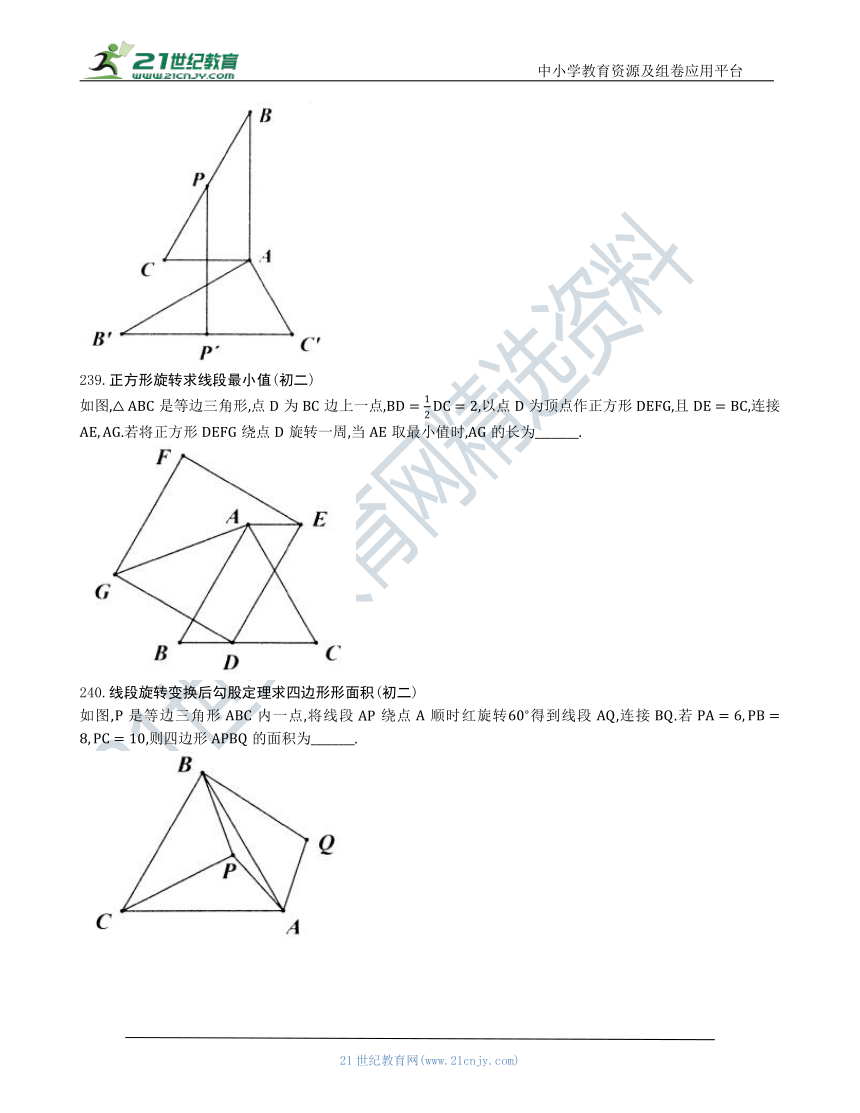
如图,是等边三角形,点为边上一点,,以点为顶点作正方形,且,连接.若将正方形绕点旋转一周,当取最小值时,的长为________.
240.线段旋转变换后勾股定理求四边形形面积(初二)
如图,是等边三角形内一点,将线段AP绕点顺时红旋转得到线段,连接.若,则四边形的面积为________.
答案
233.【解】为等边三角形,,
可将绕点逆时针旋转得,连,
且延长,作于点.如图,
,
为等边三角形,,
在中,,
为直角三角形,且,
.,
在Rt中,在Rt中,.则的面积是..故选:.
234.【解】如图,将绕点顺时针旋转得到,由旋转不变性可知:是等腰直角三角形,当的值最大时,的值最大,的最大值为的最大值为.故选:.
235.【解】连接中,,
是的中点,
在上,且半径为2,
当在的延长线上时,最大,,点是的中点,点是的中点,,,
的最大值为,故选:.
236.【解】如图,将绕点顺时针旋转得到,连接,
,
,
,
共线,连接,
在Rt中,
正方形的面积为.
237.【解】(1).
在正方形中,.
在和中,,
,故(1)正确;
(2),
又,
.即,故(2)正确;
(3)过点作的延长线丁点,如图,
.
又.
.
,
即点到直线的距离为,故(3)错误;
(4),在Rt中,,
,故(4)正确.综上所述,正确结论的序号为(1)(2)(4),故答案为:(1)(2)(4).
238.【解】将绕点顺时针旋转,
是顶角为的等腰三角形,当最小时,有最小值。即当时,有最小值,即有最小值,此时,,
线段长度的最小值,
239.【解】连接,在中,.
和都是固定值,如下图,当点在延长
线上时,,此时最小.
过点作于,
,
是等边三角形,,
,
,在Rt中,
,当点在延长线上时,.此时取最小值,
在Rt中,,在Rt中,;故答案为:8
240.【解】连接,如图,为等边三角形,
线段绕点顺时针旋转得到线段,
为等边三角形,,
,
,在和中,
在中,,
而,
为直角三角形,,
.故答案为.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十二节:旋转模型
233.线段旋转变换后,勾股定理求三角形面积(初二)
如图,为等边三角形内的一点,且到三个顶点的距离分别为3,4,5,则的面积为( )
A.
B.
C.
D.
234.旋转模型手拉手全等求最大值(初二)
如图,平面内三点,以为对角线作正方形,连接,则的最大值是( )
A.
B.
C.4
D.8
235.线段旋转过程中隐形圆求它的最大值
如图,在矩形中,点是的中点,点是的中点,连接是的中点,连接.在中,,若将绕点逆时针旋转,则在旋转的过程中,线段DG长的最大值是( )
A.
B.
C.10
D.12
236.旋转变换后勾股定理求正方形面积(初二)
如图,点是正方形内一点,且点到点的距离分别为、4,则正方形的面积为________.
237.正方形取点旋转常见的几个结论(初二)
如图,在正方形外取一点,连接,过点作垂线交于点,若.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为________.
238.直角三角形旋转求线段最小值(初二)
如图,在Rt中,,将绕点逆时针旋转得到,若为上一动点,旋转后点的对应点为点,则线段PP'长度的最小值是________.
239.正方形旋转求线段最小值(初二)
如图,是等边三角形,点为边上一点,,以点为顶点作正方形,且,连接.若将正方形绕点旋转一周,当取最小值时,的长为________.
240.线段旋转变换后勾股定理求四边形形面积(初二)
如图,是等边三角形内一点,将线段AP绕点顺时红旋转得到线段,连接.若,则四边形的面积为________.
答案
233.【解】为等边三角形,,
可将绕点逆时针旋转得,连,
且延长,作于点.如图,
,
为等边三角形,,
在中,,
为直角三角形,且,
.,
在Rt中,在Rt中,.则的面积是..故选:.
234.【解】如图,将绕点顺时针旋转得到,由旋转不变性可知:是等腰直角三角形,当的值最大时,的值最大,的最大值为的最大值为.故选:.
235.【解】连接中,,
是的中点,
在上,且半径为2,
当在的延长线上时,最大,,点是的中点,点是的中点,,,
的最大值为,故选:.
236.【解】如图,将绕点顺时针旋转得到,连接,
,
,
,
共线,连接,
在Rt中,
正方形的面积为.
237.【解】(1).
在正方形中,.
在和中,,
,故(1)正确;
(2),
又,
.即,故(2)正确;
(3)过点作的延长线丁点,如图,
.
又.
.
,
即点到直线的距离为,故(3)错误;
(4),在Rt中,,
,故(4)正确.综上所述,正确结论的序号为(1)(2)(4),故答案为:(1)(2)(4).
238.【解】将绕点顺时针旋转,
是顶角为的等腰三角形,当最小时,有最小值。即当时,有最小值,即有最小值,此时,,
线段长度的最小值,
239.【解】连接,在中,.
和都是固定值,如下图,当点在延长
线上时,,此时最小.
过点作于,
,
是等边三角形,,
,
,在Rt中,
,当点在延长线上时,.此时取最小值,
在Rt中,,在Rt中,;故答案为:8
240.【解】连接,如图,为等边三角形,
线段绕点顺时针旋转得到线段,
为等边三角形,,
,
,在和中,
在中,,
而,
为直角三角形,,
.故答案为.
21世纪教育网(www.21cnjy.com)
同课章节目录
