【中考数学几何模型】第十二节:旋转模型241-249(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十二节:旋转模型241-249(含答案) | 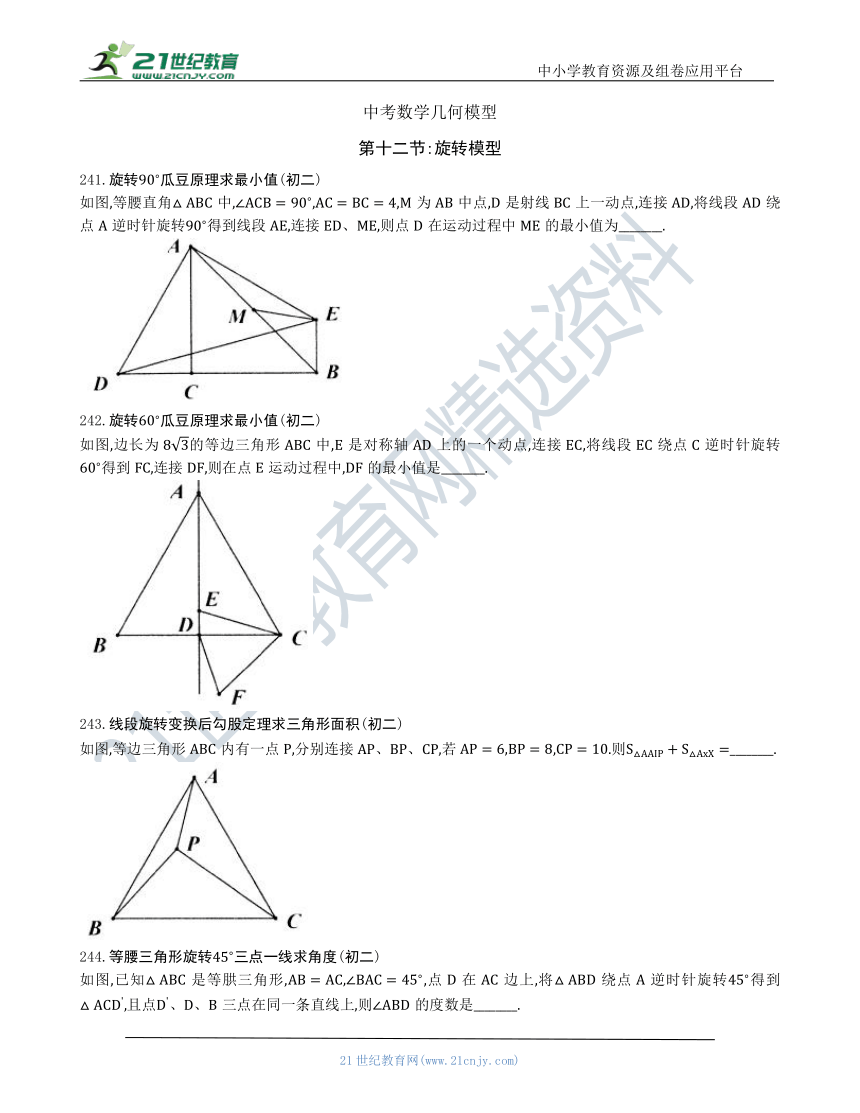 | |
| 格式 | docx | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:10:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十二节:旋转模型
241.旋转瓜豆原理求最小值(初二)
如图,等腰直角中,为中点,是射线上一动点,连接,将线段绕点逆时针旋转得到线段,连接、,则点D在运动过程中ME的最小值为________.
242.旋转瓜豆原理求最小值(初二)
如图,边长为的等边三角形中,是对称轴上的一个动点,连接,将线段绕点逆时针旋转得到,连接,则在点运动过程中,的最小值是________.
243.线段旋转变换后勾股定理求三角形面积(初二)
如图,等边三角形内有一点,分别连接,若,.则________.
244.等腰三角形旋转三点一线求角度(初二)
如图,已知是等 三角形,,点在边上,将绕点逆时针旋转得到,且点三点在同一条直线上,则的度数是________.
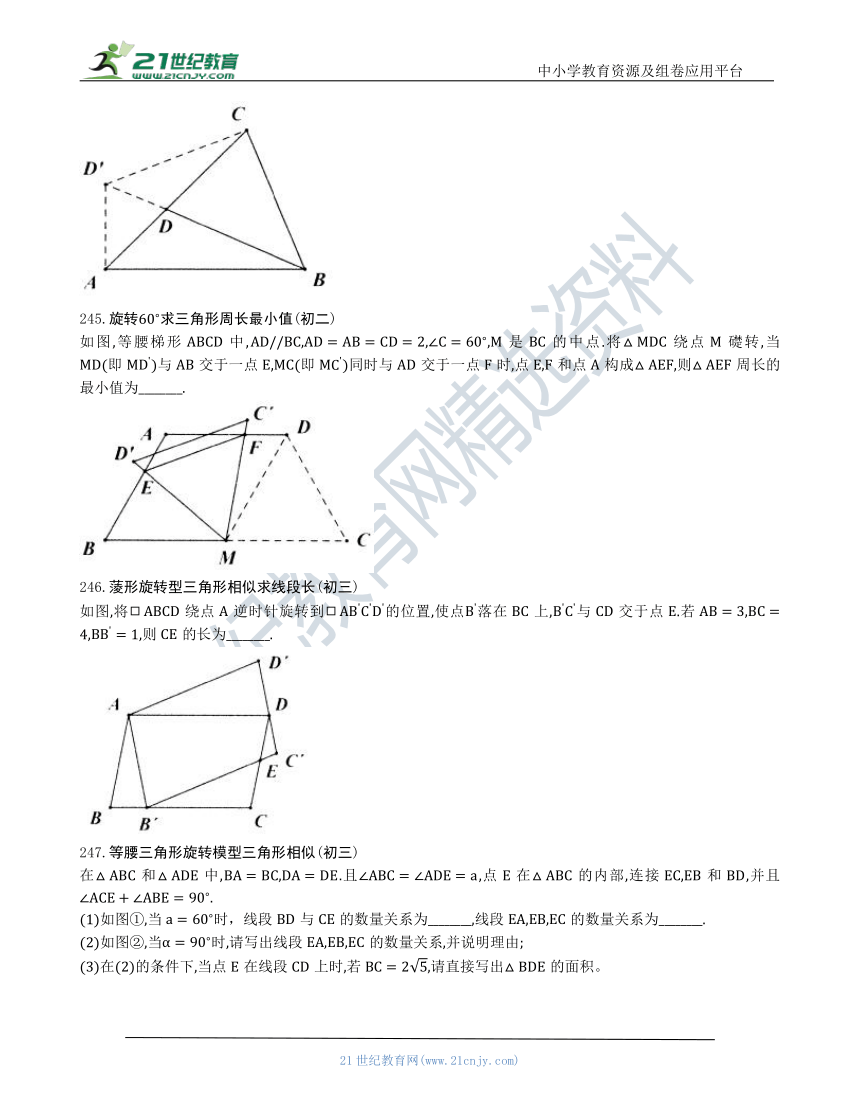
245.旋转求三角形周长最小值(初二)
如图,等腰梯形中,是的中点.将绕点礎转,当(即)与交于一点,(即)同时与交于一点时,点和点构成,则周长的最小值为________.
246.蔆形旋转型三角形相似求线段长(初三)
如图,将绕点逆时针旋转到的位置,使点落在上,与交于点.若,则的长为________.
247.等腰三角形旋转模型三角形相似(初三)
在和中,.且,点在的内部,连接和,并且.
(1)如图①,当时,线段与的数量关系为________,线段,的数量关系为________.
(2)如图②,当时,请写出线段的数量关系,并说明理由;
(3)在(2)的条件下,当点在线段上时,若,请直接写出的面积。
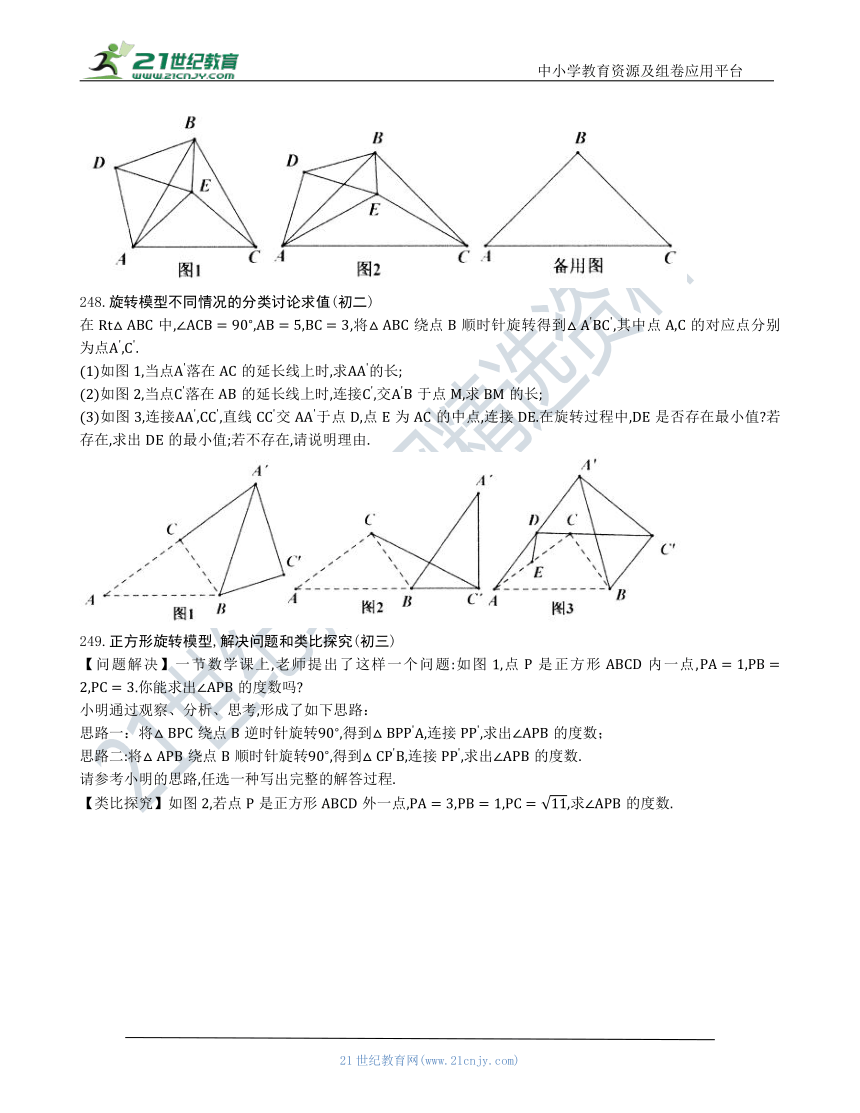
248.旋转模型不同情况的分类讨论求值(初二)
在Rt中,,将绕点顺时针旋转得到,其中点的对应点分别为点.
(1)如图1,当点落在的延长线上时,求的长;
(2)如图2,当点落在的延长线上时,连接,交于点,求BM的长;
(3)如图3,连接,直线交于点,点为的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
249.正方形旋转模型,解决问题和类比探究(初三)
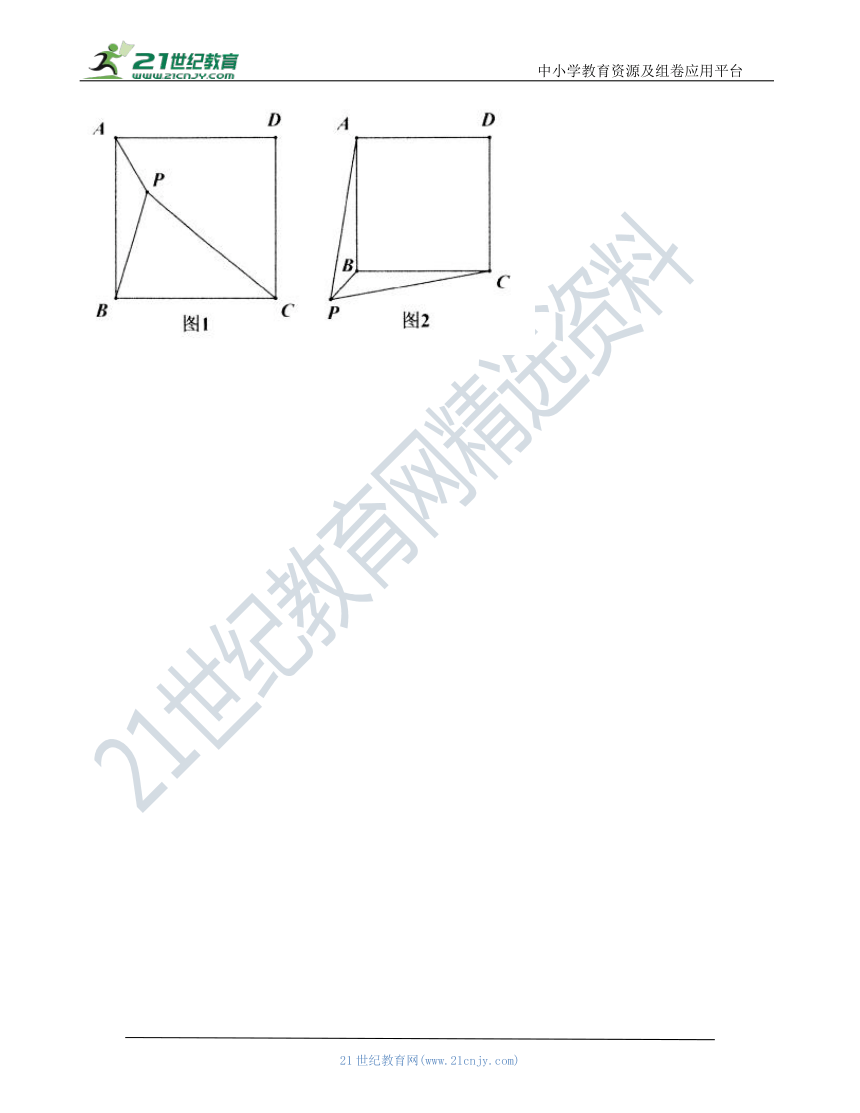
【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点是正方形内一点,.你能求出的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一:将绕点逆时针旋转,得到,连接,求出的度数;
思路二:将绕点顺时针旋转,得到,连接,求出的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】如图2,若点是正方形外一点,,求的度数.
答案
241.【解】如图,过点作的延长线于点,过点作交的延长线于点,
等腰直角中,是等腰直角三角形.
线段绕点逆时针旋转得到线段,
是等腰直角三角形,
,
,
在和中,
,
是等腰直角三角形,,
为中点,,
,
当时,的值最小,即当时,有最小值为2.故答案为2.
242.【解】如图,连接,由旋转可得,,
是等边三角形,,
,
在和中,,,
边长为8的等边三角形中,是对称轴上的个动点,,
,即点的运动轨迹为直线,
当时,最短,即为所求,此时,的最小值是,故答案为.
243.【解】如图,将绕点逆时针旋转后得,连接,根据旋转的性质可知,旋转角为等边三角形,;由旋转的性质可知,10,在中,,由勾股定理的逆定理得,是直角三角形,
.
故答案为:.
244.【解】将绕点逆时针旋转得到,故答案为:
245.【解】连接,过点作于点,过点作于点,即四边形是平行四边形,,
,,即点是的中点,四边形是平行四边形,,由勾股定理得:,
连接平行四边形是菱形,和是等边三角形,
,
在与中,,故是等边三角形,的最小值为点到的距离等于的长,即是,即的最小值是的周长的周长的最小值为,故答案为:.
246.【解】由旋转可知,,,
,,即点在同一条直线上,,又,,即,设,.故答案为:.
247.【解】(1).且都是等边三角形,,
,
,
,
,
.
故答案为.
(2)结论:.理由:如图(2)中,
.且,
都是等腰直角三角形,,
,
,,
,
,
.
(3)如图,共线,,
,
,
,
,设,
在Rt中,,
在Rt中,,
(负根已舍),,
.
248.【解】(1),
绕点顺时针旋转得到,点落在的延长线上,,Rt中,;
(2)过作交于,过作于,如图2:绕点顺时针旋转得到,,
,
Rt中,,,Rt中,,同理,;
(3)存在最小值,最小值是1,理由如下:如图3左,连接,则足的中位线,,当最小时,有最小值.如图3右,当运动到延长线上时,有最小值是的最小值是1
249.【解】(问题解决)思路一:如图1,将绕点逆时针旋转,得到,连接,,在Rt中,,根据勾股定理得,,
,是直角三角形,且;
(思路探究)如图2,将绕点逆时针旋转,得到,连接,
,
在Rt中,,
根据勾股定理得,,
,
,
是直角二角形,且,
.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十二节:旋转模型
241.旋转瓜豆原理求最小值(初二)
如图,等腰直角中,为中点,是射线上一动点,连接,将线段绕点逆时针旋转得到线段,连接、,则点D在运动过程中ME的最小值为________.
242.旋转瓜豆原理求最小值(初二)
如图,边长为的等边三角形中,是对称轴上的一个动点,连接,将线段绕点逆时针旋转得到,连接,则在点运动过程中,的最小值是________.
243.线段旋转变换后勾股定理求三角形面积(初二)
如图,等边三角形内有一点,分别连接,若,.则________.
244.等腰三角形旋转三点一线求角度(初二)
如图,已知是等 三角形,,点在边上,将绕点逆时针旋转得到,且点三点在同一条直线上,则的度数是________.
245.旋转求三角形周长最小值(初二)
如图,等腰梯形中,是的中点.将绕点礎转,当(即)与交于一点,(即)同时与交于一点时,点和点构成,则周长的最小值为________.
246.蔆形旋转型三角形相似求线段长(初三)
如图,将绕点逆时针旋转到的位置,使点落在上,与交于点.若,则的长为________.
247.等腰三角形旋转模型三角形相似(初三)
在和中,.且,点在的内部,连接和,并且.
(1)如图①,当时,线段与的数量关系为________,线段,的数量关系为________.
(2)如图②,当时,请写出线段的数量关系,并说明理由;
(3)在(2)的条件下,当点在线段上时,若,请直接写出的面积。
248.旋转模型不同情况的分类讨论求值(初二)
在Rt中,,将绕点顺时针旋转得到,其中点的对应点分别为点.
(1)如图1,当点落在的延长线上时,求的长;
(2)如图2,当点落在的延长线上时,连接,交于点,求BM的长;
(3)如图3,连接,直线交于点,点为的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
249.正方形旋转模型,解决问题和类比探究(初三)
【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点是正方形内一点,.你能求出的度数吗
小明通过观察、分析、思考,形成了如下思路:
思路一:将绕点逆时针旋转,得到,连接,求出的度数;
思路二:将绕点顺时针旋转,得到,连接,求出的度数.
请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】如图2,若点是正方形外一点,,求的度数.
答案
241.【解】如图,过点作的延长线于点,过点作交的延长线于点,
等腰直角中,是等腰直角三角形.
线段绕点逆时针旋转得到线段,
是等腰直角三角形,
,
,
在和中,
,
是等腰直角三角形,,
为中点,,
,
当时,的值最小,即当时,有最小值为2.故答案为2.
242.【解】如图,连接,由旋转可得,,
是等边三角形,,
,
在和中,,,
边长为8的等边三角形中,是对称轴上的个动点,,
,即点的运动轨迹为直线,
当时,最短,即为所求,此时,的最小值是,故答案为.
243.【解】如图,将绕点逆时针旋转后得,连接,根据旋转的性质可知,旋转角为等边三角形,;由旋转的性质可知,10,在中,,由勾股定理的逆定理得,是直角三角形,
.
故答案为:.
244.【解】将绕点逆时针旋转得到,故答案为:
245.【解】连接,过点作于点,过点作于点,即四边形是平行四边形,,
,,即点是的中点,四边形是平行四边形,,由勾股定理得:,
连接平行四边形是菱形,和是等边三角形,
,
在与中,,故是等边三角形,的最小值为点到的距离等于的长,即是,即的最小值是的周长的周长的最小值为,故答案为:.
246.【解】由旋转可知,,,
,,即点在同一条直线上,,又,,即,设,.故答案为:.
247.【解】(1).且都是等边三角形,,
,
,
,
,
.
故答案为.
(2)结论:.理由:如图(2)中,
.且,
都是等腰直角三角形,,
,
,,
,
,
.
(3)如图,共线,,
,
,
,
,设,
在Rt中,,
在Rt中,,
(负根已舍),,
.
248.【解】(1),
绕点顺时针旋转得到,点落在的延长线上,,Rt中,;
(2)过作交于,过作于,如图2:绕点顺时针旋转得到,,
,
Rt中,,,Rt中,,同理,;
(3)存在最小值,最小值是1,理由如下:如图3左,连接,则足的中位线,,当最小时,有最小值.如图3右,当运动到延长线上时,有最小值是的最小值是1
249.【解】(问题解决)思路一:如图1,将绕点逆时针旋转,得到,连接,,在Rt中,,根据勾股定理得,,
,是直角三角形,且;
(思路探究)如图2,将绕点逆时针旋转,得到,连接,
,
在Rt中,,
根据勾股定理得,,
,
,
是直角二角形,且,
.
21世纪教育网(www.21cnjy.com)
同课章节目录
