2023年九年级冲刺中考数学几何压轴题:几何探究问题(含答案)
文档属性
| 名称 | 2023年九年级冲刺中考数学几何压轴题:几何探究问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 16:52:41 | ||
图片预览



文档简介
中考数学几何压轴题:几何探究问题
1.【教材呈现】
(1)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠G=90°,BC=6,若△ABC固定不动,将△AFG绕点A旋转,边AF、AG与边BC分别交于点D,E(点D不与点B重合,点E不与点C重合)
①求证:AE2=DE BE;
②求BE CD的值;
【拓展探究】
(2)如图2,在△ABC中,∠C=90°,点D,E在边BC上,∠B=∠DAE=30°,且,请直接写出的值.
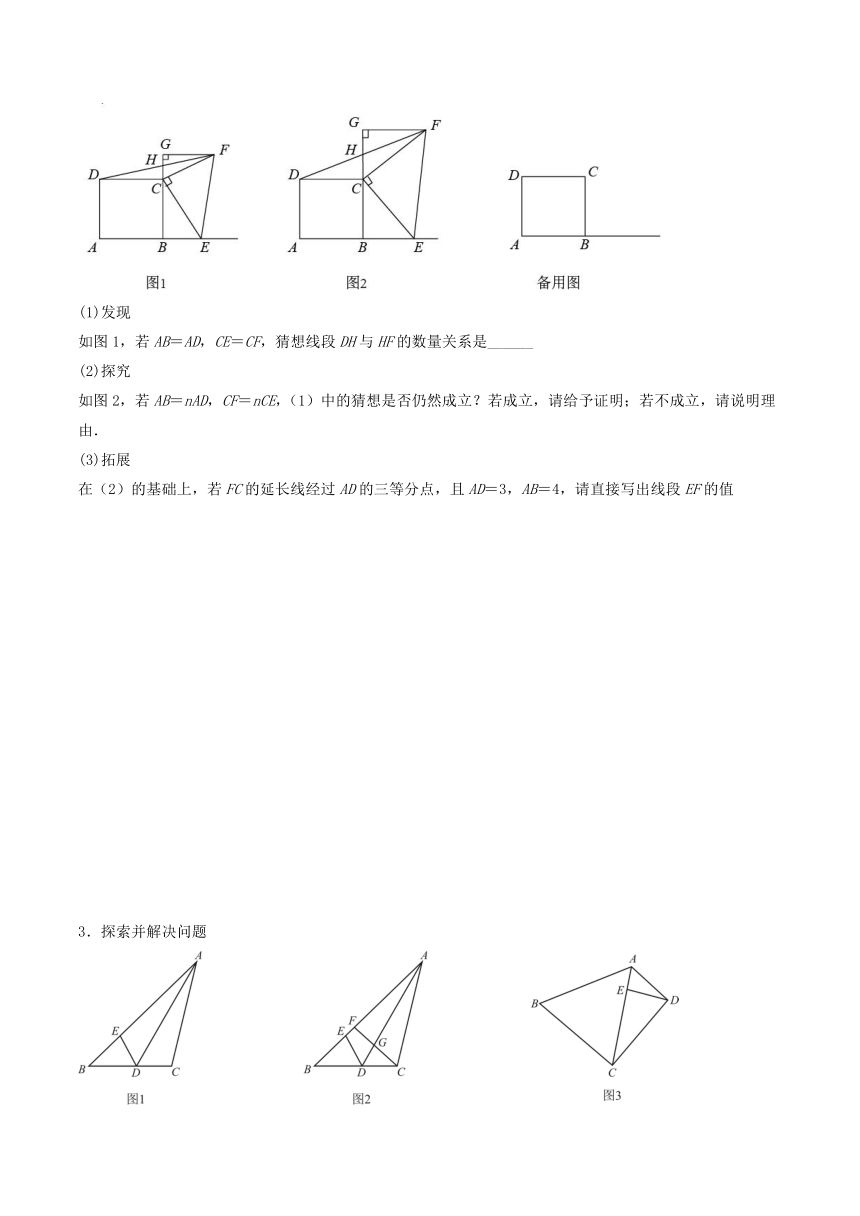
2.点E是矩形ABCD边AB延长线上一动点(不与点B重合),在矩形ABCD外作Rt△ECF其中∠ECF=90°,过点F作FG⊥BC交BC的延长线于点G,连接 DF交CG于点H.
(1)发现
如图1,若AB=AD,CE=CF,猜想线段DH与HF的数量关系是______
(2)探究
如图2,若AB=nAD,CF=nCE,(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)拓展
在(2)的基础上,若FC的延长线经过AD的三等分点,且AD=3,AB=4,请直接写出线段EF的值
3.探索并解决问题
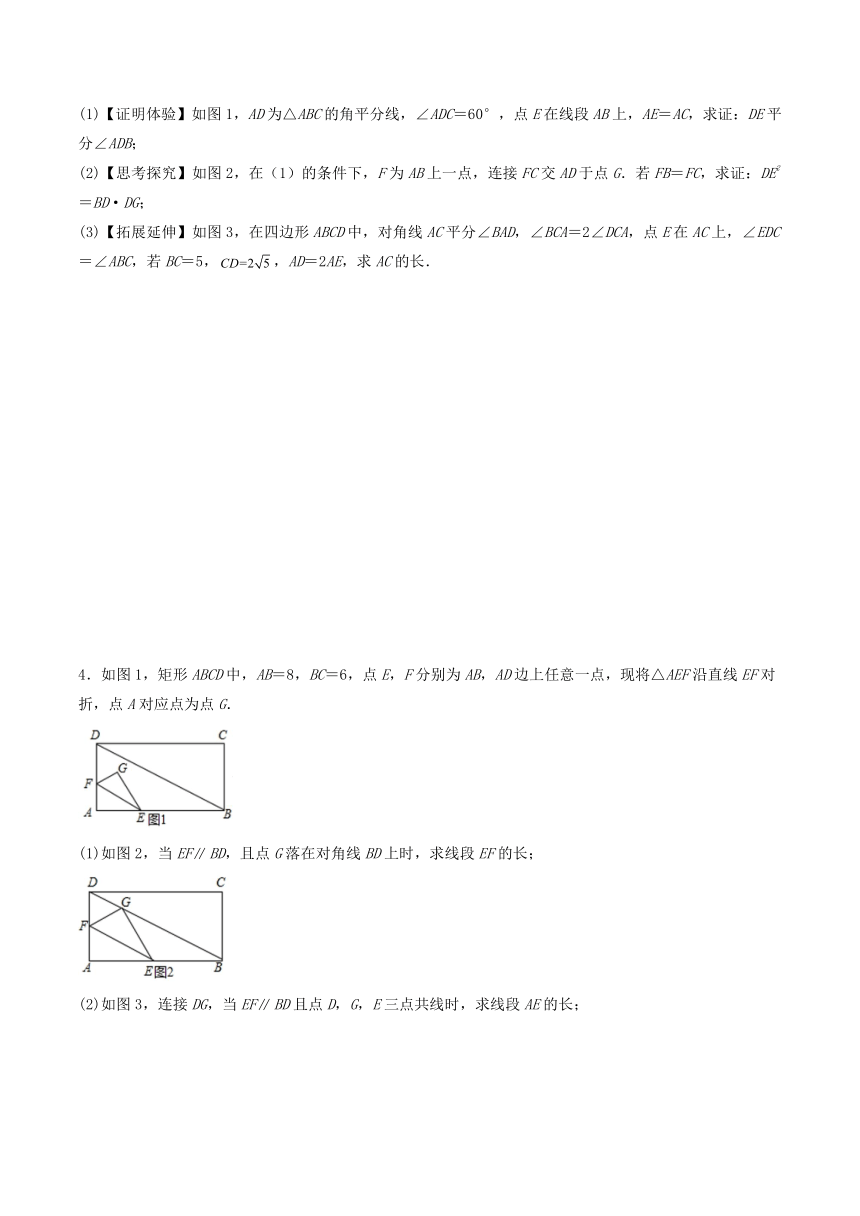
(1)【证明体验】如图1,AD为△ABC的角平分线,∠ADC=60°,点E在线段AB上,AE=AC,求证:DE平分∠ADB;
(2)【思考探究】如图2,在(1)的条件下,F为AB上一点,连接FC交AD于点G.若FB=FC,求证:DE2=BD·DG;
(3)【拓展延伸】如图3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC,若BC=5,,AD=2AE,求AC的长.
4.如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
(1)如图2,当EFBD,且点G落在对角线BD上时,求线段EF的长;
(2)如图3,连接DG,当EFBD且点D,G,E三点共线时,求线段AE的长;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出线段AE的长;若不存在,请说明理由.
5.综合与实践 探究特殊三角形中的相关问题
问题情境:
某校学习小组在探究学习过程中,将两块完全相同的且含60°角的直角三角板ABC和AFE按如图1所示位置放置,且Rt△ABC的较短直角边AB为2,现将Rt△AEF绕A点按逆时针方向旋转,如图2,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)初步探究:
勤思小组的同学提出:当旋转角α=______ 时,△AMC是等腰三角形;
(2)深入探究:
敏学小组的同学提出在旋转过程中.如果连接AP,CE,那么AP所在的直线是线段CE的垂直平分线,请帮他们证明;
(3)再探究:
在旋转过程中,当旋转角α=30°时,求△ABC与△AFE重叠的面积;
(4)拓展延伸:
在旋转过程中,△CPN是否能成为直角三角形?若能,直接写出旋转角α的度数;若不能,说明理由.
6.【发现问题】
(1)如图1,已知和△CDE均为等边三角形,在上,在上,易得线段和的数量关系是_________.
(2)将图1中的△CDE绕点旋转到图2的位置,直线和直线交于点.
①判断线段和的数量关系,并证明你的结论;
②图2中的度数是______.
(3)【探究拓展】如图3,若和△CDE均为等腰直角三角形,,,,直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
7.综合与探究
(1)发现
如图1,△ABC是等边三角形,点在边上(不与,重合),连接,将绕点逆时针旋转得到,连接、.
填空:
①的度数是______.
②线段、、之间的数量关系是______________.
(2)探究
如图2,△ABC是等腰直角三角形,,,点在边上(不与、重合),连接,将绕点逆时针旋转得到,连接、.腾飞学习小组类比问题(1)猜出,请你帮助他们说明理由.
(3)应用
如图3,在Rt△ABC中,,,,,请直接写出的长.
8.【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)请你判断AM,AD,MC三条线段的数量关系,并说明理由;
(2)AM = DE + BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否仍然成立?请分别作出判断,不需要证明.
9.综合与实践
动手操作:某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘.
如图1,△ACB是等腰直角三角形,AC=BC=4,∠ACB=90°,将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C,过点A′作A′D⊥CB交CB延长线于点D.
思考探索:(1)在图1中:
①CD=_______ ;
②△A′BC的面积为_________ ;
拓展延伸:(2)如图2,若△ACB为任意直角三角形,∠ACB=90°.将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C,过点A′作A′D⊥CB交CB延长线于点D.猜想三条线段AC、CD、A′D的数量关系,并证明.
(3)如图3,在△ACB中,AB=AC=5,BC=6,将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C.
①△A′BC的面积为______ .
②若点D是△ACB的边BC的高线上的一动点,连接A′D、DB,则A′D+DB的最小值是______ .
10.综合与实践
在△ABC中,BD⊥AC于点D,点P为射线BD上任一点(点B除外),连接AP,将线段PA绕点P顺时针方向旋转α,α=∠ABC,得到PE,连接CE.
(1)如图1,当BA=BC,且∠ABC=60°时,BP与CE的数量关系是 ,BC与CE的位置关系是
(2)如图2,当BA=BC,且∠ABC=90°时,(1)中的结论是否成立?若成立,请予以证明;若不成立,请说明理由.(请选择图2,图3中的一种情况予以证明或说理)
(3)在(2)的条件下,若AB=8,AP=,请直接写出CE的长.
11.(1)[问题发现]
如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为BC的中点,以CD为一条边作正方形CDEP,点E恰好与点A重合.则线段BE与AF的数量关系为______ ;
(2)[拓展研究]
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请就图2的情形给出证明;
(3)[问题发现]
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
12.如图1,在Rt△ABC中,∠ACB=90°,CA=CB,点D为AB边上一动点,连接CD,并将CD绕点C逆时针旋转90°得到CE,连接BE、DE,点F为DE中点,连接BF.
(1)求证:△ACD△BCE;
(2)如图2所示,在点D的运动过程中,当时(n>1),分别延长AC、BF相交于G:
①当时,求CG与AB的数量关系;
②当=n时(n>1),= ______ .
(3)当点D运动时,在线段CD上存在一点M,使得AM+BM+CM的值最小,若CM=2,则BE= ______.
13.如图1,在中,∠B=90°,,,点分别是边的中点,连接.将△CDE绕点逆时针方向旋转,记旋转角为.
(1)问题发现
当时,______;当时,______.
(2)拓展探究
试判断:当时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点逆时针旋转至三点在同一条直线上时,请直接写出线段的长______.
14.(1)问题探究:如图1,在正方形,点,分别在边,上,于点,点,分别在边、上,.
①判断与的数量关系:______;
②推断:的值为:______ ;(无需证明)
(2)类比探究:如图(2),在矩形中,.将矩形沿折叠,使点落在边上的点处,得到四边形,交于点,连接交于点.试探究与之间的数量关系,并说明理由;
(3)拓展应用1:如图3,四边形中,,,,,点,分别在边、上,求的值.
(4)拓展应用2:如图2,在(2)的条件下,连接,若,,求的长.
15.【问题背景】
在四边形中,,,E、F分别是、上的点,且,试探究图1中线段、、之间的数量关系.
【初步探索】
小亮同学认为:延长到点G,使,连接,再证明,则可得到、、之间的数量关系是___________.
【探索延伸】
在四边形中如图2,,,E、F分别是、上的点,,上述结论是否仍然成立?
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角()为70°,试求此时两舰艇之间的距离.
参考答案:
1.解:(1)①∵△ABC和△AGF都是等腰直角三角形,∠BAC=∠G=90°,
∴∠B=∠C=∠GAF=45°,
又∵∠AED=∠NEA,
∴△ABE∽△DAE,
∴,
∴;
②∵∠DAC=∠DAE+∠CAE,∠AEB=∠C+∠CAE,∠C=∠DAE=45°,
∴∠AEB=∠DAC,
又∵∠B=∠C,
∴△AEB∽△DAC,
∴,
∴,
∵AB=AC,∠BAC=90°,BC=6,
∴,即,
∴,
∴;
(2)∵,
∴可设,,
∵∠B=∠DAE=30°,∠ADE=∠BDA,
∴△ADE∽△BDA,
∴,
∴,
可设,,
∴,
∵∠B=30°,∠ACB=90°,
∴,
∴,
∴
在直角△ACD中,,
∴,
∴,
∴.
2.(1),理由如下:
∵四边形ABCD是矩形,,
∴四边形ABCD是正方形,
∴,,
∵,,
∴,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴,
,
在和中,
,
∴,
∴,
故答案为,
(2)仍然成立,理由如下:
∵四边形ABCD是矩形,,,
∴
∴,
∵,
∴,
∴,
∴,
∴四边形ABCD是矩形,,
∴,
∴,
∴,
∵四边形ABCD是矩形,
∴,
∵,
∴,
∴,,
在和中,
,
∴,
∴,
(3)如图所示,延长FC交AD于R,
∵四边形ABCD是矩形,
∴,,,,
∵,,
∴,
∴,
分两种情况:
①当时,
∵,
∴,,
在中,由勾股定理得:
,
∵,,
∴,
∴,
由勾股定理得:EF=;
②当时,同理可得:,
,,
,
由勾股定理得:
,
综上所说,若射线FC过AD的三等分点,,,
则线段EF的长为或.
3.(1)证明:∵平分,
∴,
∵,,
∴,
∴,
∴,
∴,即DE平分;
(2)证明:∵,
∴,
∵,
∴,
∴,
由(1)知,
∴,
∴;
(3)解:如图3,在AB上取一点F使AF=AD,连接CF,
∵平分,
∴,
∵,
∴,
∴,,,
∵,
∴,
∵,
∴,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,即
4.(1)解:如图,连接AG,
由折叠性质得AG⊥EF,
∵EFBD,
∴AG⊥BD,
在矩形ABCD中,AB=8,BC=6,
∴∠DAB=90°,AD=BC=6,
∴DB==10,
∵△GEF是由△AEF沿直线EF对折而成,
∴△GEF≌△AEF,
∴EF为AG中垂线,
∵EFBD,
∴EF=BD=5;
(2)解:∵点D,G,E三点共线,
∴∠DGF=90°,
设AF=3t,则FG=3t,AE=4t,DF=6-3t,
在Rt△DFG中,,即=36-36t,
∵tan∠FDG=,
∴,∴t=,∴AE=;
(3)解:①当△AEF∽△GHE时,如图,过点H作HP⊥AB于P,
∵∠AEF=∠FEG=∠EHG,∠EHG+∠HEG=90°,
∴∠FEG+∠HEG=90°,
∴∠A=∠FEH=90°,
∴△AEF∽△EHF,
∴EF:HE=AF:AE=1:2,
∵∠A=∠HPE=90°,
∴∠AEF+∠HEP=90°,∠HEP+∠EHP=90°,
∴∠AEF=∠EHP,
∴△AEF∽△HPE,
∴AE:HP=EF:EH=1:2,
∴HP=6,
∴AE=3;
②当△AEF∽△GHE时,如图,过点H作HP⊥AB于P,
同理可得EF:HE=1:2,EA:HP=1:2,
设AF=t,则AE=2t,EP=2t,HP=4t,BP=8-4t,
∵△BHP∽△BDA,
∴4t:6=(8-4t):8,
∴t=,
∴AE=;
③当△AEF∽△GEH时,如图,过点G作MNAB交AD于点M,过点E作EN⊥MN于N,
设AF=t,则AE=2t,DF=6-t,
由折叠可知,△AEF≌△GEF,
∴AE=GE,
∵△AEF∽△GEH,AE=GE,
∴△AEF≌△GEH(AAS),
∴FG=GH,
∵MGDH,
∴FM=(6-t),
∴AN=EN=AF+FM=,
∵△FMG∽△GNE,GF:GE=1:2,
∴MG=NE=AM=,GH=2FN=6-t,
∵MN=AE,
∴+6-t=2t,
∴t=,
∴AE=;
④当△AEF∽△GEH时,如图,过点G作MNAB交AD于点M,过点E作EN⊥MN于N,过点H作HQ⊥AD于Q,
设AF=t,则AE=2t,
设FM=a,则NG=2a,NE=a+t,
∴MG=EN=AM=,
∴+2a=2t,
由上题知,MF=MQ=a,QH=2MG=a+t,
∴DQ=6-t-2a,
∵,
∴,
∴t=,
∴AE=.
综上,满足条件取线段AE的长为:3或或或.
5.(1)当AM=CM,即∠CAM=∠C=30°时,△AMC是等腰三角形;
∵∠BAC=90°,
∴α=90° 30°=60°,
当AM=CM,即∠CAM=∠CMA时,△AMC是等腰三角形,
∵∠C=30°,
∴∠CAM=∠AMC=75°,
∵∠BAC=90°,
∴α=15°,
综上所述,当旋转角α=60°或15°时,△AMC是等腰三角形,
故答案为:60°或15°;
(2)由题意可知,AB=AF,∠B=∠F,∠E=∠C,AE=AC,
∵现将Rt△AEF绕A点按逆时针方向旋转α(0°<α<90°),
∴∠BAM=∠FAN,
在△ABM与△AFN中,
,
∴,
∴AM=AN,
∵AE=AC,
∴EM=CN,
在和中
,
∴,
∴PE=PC,
∴点P在CE的垂直平分线上,
∵AE=AC,
∴点A在CE的垂直平分线上,
∴AP所在的直线是线段CE的垂直平分线;
(3)∵α=30°,∠B=60°,
∴∠AMB=90°,
∴△ABM是直角三角形,
∵AB=2,
∴BM=AB sin30°=1,AM=AB cos30°=,
∴=AM MB=1×=,
∵AE=AC=AB tan60°=2,AM=,
∴EM=,
在和中
∴,
由(2)可知,
∴=,
∵AF AE=×2×2=2,
∴△ABC与△AFE重叠的面积2 2×=;
(4)如答题图1所示:当∠CNP=90°时.
∵∠CNP=90°,
∴∠ANF=90°.
又∵∠AFN=60°,
∴∠FAN=180° 60° 90°=30°.
∴∠α=30°.
如答题图2所示:当∠CPN=90°时.
∵∠C=30°,∠CPN=90°,
∴∠CNP=60°.
∴∠ANF=60°.
又∵∠F=60°,
∴∠FAN=60°.
∴∠α=60°.
综上所述,∠α=30°或60°.
6.(1)解:∵和均为等边三角形,
∴,,
∴,
故答案为:;
(2)如图2中,
①∵和均为等边三角形,
∴,,,
∴,
∴(SAS),
∴;
②∵,
∴,
设交于点.
∵,
∴,
∴,
故答案为:;
(3)结论:,.
理由:如图3中,
∵,,,
∴,,
∴,
∴,,
∴,
∵,
∴.
7.(1)①∵AE是AD绕点A逆时针旋转60°而得到的
∴AD=AE,∠DAE=60°
∵△ABC是等边三角形
∴AB=AC=BC,∠B=∠BAC=60°
∴∠BAD+∠DAC=∠DAC+∠CAE=60°
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠ACE=∠B=60°
故答案为:60°
②由①知:△ABD≌△ACE
∴BD=CE
∴CA=BC=BD+CD=CE+CD
故答案为:CA=CE+CD
(2)理由如下:
∵AE是AD绕点A逆时针旋转90°而得到的
∴AD=AE,∠DAE=90°
∵AB=AC,
∴由勾股定理得:
∵
∴∠BAD+∠DAC=∠DAC+∠CAE=90°
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
∴BC=BD+CD=CE+CD
∴
(3)如图,在线段CD上取CE=BD,连接AE,设AB、CD交于点F
∵∠BAC=∠CAE=90°,∠BFD=∠CFA
∴∠DBA=∠ECA
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴AD=AE,∠DAB=∠EAC
∴∠DAE=∠DAB+∠BAE=∠EAC+∠BAE=∠BAC=90°
∴△ADE是等腰直角三角形
∴由勾股定理得:
∴
∵,
∴由勾股定理得:
∵BD=5,
∴在Rt△BDC中,由勾股定理得:CD=
∵
∴
解得:
8.解:(1)AM=AD+MC.理由如下:
如图1(1)所示,分别延长AE,BC交于点N,
∵四边形ABCD是正方形,
∴ADBC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
∵E是CD的中点,
∴DE=CE,
在ADE与NCE中,
∴ADE≌NCE(AAS),
∴AD=NC,
∵MN=NC+MC,
∴AM=AD+MC;
(2)AM=DE+BM成立.理由如下:
如图1(2)所示,将ADE绕点A顺时针旋转90°,得到ABF,
∵四边形ABCD是正方形,
∴ABDC,∠D=∠ABM=90°,
∴∠AED=∠BAE,
∵旋转,
∴∠F=∠AED,∠FAB=∠EAD,BF=ED,∠D=∠ABF=90°,
∴∠ABM+∠ABF=180°,
∴点F、B、M在同一直线上,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠BAF=∠MAE,
∵∠BAE=∠BAM+∠MAE,
∴∠AED=∠BAM+∠BAF=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∵FM=BF+BM
∴AM=DE+BM;
(3)①结论AM=AD+MC仍然成立,理由如下:
①如图2(1),延长、交于点,
四边形是矩形,
.
.
平分,
.
.
.
在ADE与PCE中,
;∴ADE≌PCE(AAS),
.
∵MP=PC+MC,
∴AM=AD+MC;
②结论不成立,理由如下:
假设成立.
过点作,交的延长线于点,如图2(2)所示.
四边形是矩形,
,.
,
.
.
.
,
.
,
,
.
.
.
,
.
,
与条件“ “矛盾,故假设不成立.
不成立.
9.解:(1)①∵边AB绕点B顺时针旋转得到线段,
∴,.
∵AC=BC=4,,
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∴BD=AC=4.
∴CD=BC+BD=8.
故答案为:8.
②∵,
∴.
∴.故答案为:8.
(2),证明如下:
∵边AB绕点B顺时针旋转得到线段,
∴,.
∴.
∵,
∴.
∴.
∵,
∴.
∴.
∴.
∴,BD=AC.
∴.
(3)如下图所示,过点作交CB延长线于点F,过点A作交CB于点E,交线段于点M,再连接DC.
①∵AB=AC=5,BC=6,且,
∴,.
∴.
∵边AB绕点B顺时针旋转得到线段,
∴,.
∴.
∴.
∵,
∴.
∴.
∴.
∴.
∴.
故答案为:9.
②∵,且BE=CE,
∴AE垂直平分CB.
∴DC=DB.
∴.
∵点D在AE上,
∴.
∴当点D与点M重合时,有最小值,此时最小值为.
∵,,
∴.
∵BC=6,
∴CF=BC+BF=10.
∴.
∴的最小值为.
故答案为:.
10.解:(1)BP=CE,BC⊥CE,理由如下:
如图所示,连接AE,
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=∠ACB=60°,
由旋转的性质得,PA=PB,,
∴△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP+∠PAD=∠CAE+∠APD,即∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE,
∵BD⊥AC,△ABC是等边三角形,
∴,
∴∠ACE=30°,
∴∠BCE=∠ACE+∠ACB=90°,
∴BC⊥CE;
故答案为:BP=CE,BC⊥CE;
(2)(1)中结论BC⊥CE仍然成立,BP=CE不成立,结论是,理由如下:
如图所示,连接AE,
∵AB=BC,∠ABC=90°,
∴,∠BAC=∠BCA=45°,
由旋转的性质得,PA=PB,,
∴,∠PAE=∠PEA=45°,
∴∠BAP+∠PAD=∠CAE+∠PAD,即∠BAP=∠CAE,
∵,
∴△BAP∽△CAE,
∴,∠ACE=∠ABP,
∴,
∵AB=BC,BD⊥AC,
∴,
∴∠ACE=45°,
∴∠BCE=∠ACE+∠ACB=90°,
∴BC⊥CE;
(3)如图2所示,当P在线段BD上时,
∵AB=BC=8,∠ABC=90°,
∴,∠BAD=45°,
∵BD⊥AC,
∴,,
∴∠ABD=∠BAD,
∴,
∵,
∴,
∴,
∴;
如图3所示,当P在BD延长线上时,连接AE,
同理可证∠BAC=∠PAE=45°,
∴∠BAD+∠PAD=∠PAE+∠PAD,即∠BAP=∠CAE,
同理可得,
∴△BAP∽△CAE,
∴,
∴,
同理可求得,,
∴,
.
∴综上所述,CE=2或14.
11.解:(1)在Rt△ABC中,AB=AC=4,
根据勾股定理得,BC=AB=4,
点D为BC的中点,
∴AD=BC=2,
∵四边形CDEF是正方形,
∴AF=EF=AD=2,
∵BE=AB=4,
∴BE=AF,
故答案为BE=AF;
(2)无变化;
如图2,在Rt△ABC中,AB=AC=4,
∴∠ABC=∠ACB=45°,
∴sin∠ABC==,
在正方形CDEF中,∠FEC=∠FED=45°,
在Rt△CEF中,sin∠FEC==,
∴=,
∵∠FCE=∠ACB=45°,
∴∠FCE+∠ACE=∠ACB+∠ACE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴==,
∴BE=AF,
∴线段BE与AF的数量关系无变化;
(3)当点E在线段AF上时,
由(1)知,CF=EF=CD=2,
在Rt△BCF中,CF=2,BC=4,
根据勾股定理得,BF=2,
∴BE=BF﹣EF=2﹣2,
由(2)知,BE=AF,
∴AF=2﹣2,
当点E在线段BF的延长线上时,如图3,
在Rt△ABC中,AB=AC=4,
∴∠ABC=∠ACB=45°,
∴sin∠ABC==,
在正方形CDEF中,∠FEC=∠FED=45°,
在Rt△CEF中,sin∠FEC==,
∴=,
∵∠FCE=∠ACB=45°,
∴∠FCB+∠ACB=∠FCB+∠FCE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴==,
∴BE=AF,
由(1)知,CF=EF=CD=2,
在Rt△BCF中,CF=2,BC=4,
根据勾股定理得,BF=2,
∴BE=BF+EF=2+2,
由(2)知,BE=AF,
∴AF=2+2.
即:当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为2﹣2或2+2.
12.(1)证明:∵把CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=∠DCB+∠ECB=90°.
又∵∠ACB=90°=∠ACD+∠DCB,
∴∠ACD=∠ECB,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS);
(2)①∵∠ACB=90°,CA=CB,
∴∠A=∠CBA=45°,
∵△ACD≌△BCE,
∴∠A=∠CBE=45°,
∴∠DBE=90°,
∵=,
过点G作GH⊥AB,
∵点F为DE中点,
∴DF=FB=,
∴∠FDB=∠FBD,
∴tan∠FDB=tan∠FBD,
∴,
∵∠A=45°,
∴是等腰直角三角形,
∴GH=AH,
∴,此时,H、D重合,
∴设AD=3x,BD=2x,则AB=5x,AC=BC=5x÷=,
∴GH=AH=3x,AG=3x
∴CG=3x-=,
∴
②当=n时(n>1),
设AD=nx,BD=x,则AB=(n+1)x,AC=BC=(n+1)x÷=,
同理:GH=AH=nx,AG=nx
∴CG=nx-=,
∴=,
故答案是:;
(3)如图,把绕点A顺时针旋转60°,得到,
∴AM=AG,BM=HG,∠MAG=60°,
∴是等边三角形,
∴MA=MG,
∴AM+BM+CM= HG+MG+CM,当点C、M、G、H四点共线时,AM+BM+CM的值最小,
连接BH,
∵把绕点A顺时针旋转60°,得到,
∴AM=AG,AB=AH,∠MAG=60°,
∴是等边三角形,是等边三角形,
∴∠AMG=∠AGM=60°,AH=BH,
∵AC=BC,
∴CH垂直平分AB,即CD垂直平分AB,
∴∠MAD=30°,
设AD=a,则MD=,
∵CM=2,AD=CD,
∴+2=a,解得:a=3+,
∴BE=AD=3+.
故答案是:3+.
13.(1)解:当时,
Rt中,∠B=90°,
,
点分别是边的中点,
,,
,
故答案为:;
如图,
当时,可得,
,
,
故答案为:;
(2)解:如图,
当时,的大小没有变化,
,
,
,
,
;
(3)解:如图,当点在的延长线上时,
在Rt中,,,
,
,
,
;
如图,当点在线段上时,
在Rt中,,,
,
,
,
,
综上所述,满足条件的的长为或.
14.解:(1)①证明:四边形是正方形,
,.
.
,
.
.
,
.
故答案为:.
②结论:.
理由:,,
,
,
四边形是平行四边形,
,
,
,
.
故答案为:1.
(2)结论:.
理由:如图2中,过点作于.
,
,
,,
,
,
,
,
四边形是矩形,
,
.
(3)如图3,过点作,交的延长线于点,过点作,连接,
,,,
四边形是矩形,
,,,
,,,
,
,
,且,
,且,
,
,
,,
,
,
(不合题意,舍去),,
,
由(2)的结论可知:.
(4)解:如图2中,过点作交的延长线于.
,
假设,,,
,,
,
,
或(舍弃),
,,
,
,
,,
,
,,
,
,
,
,
,,
,
.
15.证明:(初步探索)如图1,延长到点G,使,连接,
在和中
,
在和中
∴,
∵,
∴;
(探索延伸)证明:如图,延长到点G,使,连接,
则:,
∵,
∴,
在和中
;∴(SAS),
∴,
∵,
∴,
∴,即:,
在和中
;∴(SAS),
∴,
∵,
∴;
(结论运用)解:连接,延长、相交于点,
,
又,
∴图形符合探索延伸中的条件,
∴结论,成立,
∵,
∴(海里);
∴两舰艇之间的距离为:210海里.
1.【教材呈现】
(1)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠G=90°,BC=6,若△ABC固定不动,将△AFG绕点A旋转,边AF、AG与边BC分别交于点D,E(点D不与点B重合,点E不与点C重合)
①求证:AE2=DE BE;
②求BE CD的值;
【拓展探究】
(2)如图2,在△ABC中,∠C=90°,点D,E在边BC上,∠B=∠DAE=30°,且,请直接写出的值.
2.点E是矩形ABCD边AB延长线上一动点(不与点B重合),在矩形ABCD外作Rt△ECF其中∠ECF=90°,过点F作FG⊥BC交BC的延长线于点G,连接 DF交CG于点H.
(1)发现
如图1,若AB=AD,CE=CF,猜想线段DH与HF的数量关系是______
(2)探究
如图2,若AB=nAD,CF=nCE,(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)拓展
在(2)的基础上,若FC的延长线经过AD的三等分点,且AD=3,AB=4,请直接写出线段EF的值
3.探索并解决问题
(1)【证明体验】如图1,AD为△ABC的角平分线,∠ADC=60°,点E在线段AB上,AE=AC,求证:DE平分∠ADB;
(2)【思考探究】如图2,在(1)的条件下,F为AB上一点,连接FC交AD于点G.若FB=FC,求证:DE2=BD·DG;
(3)【拓展延伸】如图3,在四边形ABCD中,对角线AC平分∠BAD,∠BCA=2∠DCA,点E在AC上,∠EDC=∠ABC,若BC=5,,AD=2AE,求AC的长.
4.如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
(1)如图2,当EFBD,且点G落在对角线BD上时,求线段EF的长;
(2)如图3,连接DG,当EFBD且点D,G,E三点共线时,求线段AE的长;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出线段AE的长;若不存在,请说明理由.
5.综合与实践 探究特殊三角形中的相关问题
问题情境:
某校学习小组在探究学习过程中,将两块完全相同的且含60°角的直角三角板ABC和AFE按如图1所示位置放置,且Rt△ABC的较短直角边AB为2,现将Rt△AEF绕A点按逆时针方向旋转,如图2,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)初步探究:
勤思小组的同学提出:当旋转角α=______ 时,△AMC是等腰三角形;
(2)深入探究:
敏学小组的同学提出在旋转过程中.如果连接AP,CE,那么AP所在的直线是线段CE的垂直平分线,请帮他们证明;
(3)再探究:
在旋转过程中,当旋转角α=30°时,求△ABC与△AFE重叠的面积;
(4)拓展延伸:
在旋转过程中,△CPN是否能成为直角三角形?若能,直接写出旋转角α的度数;若不能,说明理由.
6.【发现问题】
(1)如图1,已知和△CDE均为等边三角形,在上,在上,易得线段和的数量关系是_________.
(2)将图1中的△CDE绕点旋转到图2的位置,直线和直线交于点.
①判断线段和的数量关系,并证明你的结论;
②图2中的度数是______.
(3)【探究拓展】如图3,若和△CDE均为等腰直角三角形,,,,直线和直线交于点,分别写出的度数,线段、间的数量关系,并说明理由.
7.综合与探究
(1)发现
如图1,△ABC是等边三角形,点在边上(不与,重合),连接,将绕点逆时针旋转得到,连接、.
填空:
①的度数是______.
②线段、、之间的数量关系是______________.
(2)探究
如图2,△ABC是等腰直角三角形,,,点在边上(不与、重合),连接,将绕点逆时针旋转得到,连接、.腾飞学习小组类比问题(1)猜出,请你帮助他们说明理由.
(3)应用
如图3,在Rt△ABC中,,,,,请直接写出的长.
8.【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
(1)请你判断AM,AD,MC三条线段的数量关系,并说明理由;
(2)AM = DE + BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否仍然成立?请分别作出判断,不需要证明.
9.综合与实践
动手操作:某数学课外活动小组利用图形的旋转探究图形变换中蕴含的数学奥秘.
如图1,△ACB是等腰直角三角形,AC=BC=4,∠ACB=90°,将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C,过点A′作A′D⊥CB交CB延长线于点D.
思考探索:(1)在图1中:
①CD=_______ ;
②△A′BC的面积为_________ ;
拓展延伸:(2)如图2,若△ACB为任意直角三角形,∠ACB=90°.将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C,过点A′作A′D⊥CB交CB延长线于点D.猜想三条线段AC、CD、A′D的数量关系,并证明.
(3)如图3,在△ACB中,AB=AC=5,BC=6,将边AB绕点B顺时针旋转90°得到线段A′B,连接A′C.
①△A′BC的面积为______ .
②若点D是△ACB的边BC的高线上的一动点,连接A′D、DB,则A′D+DB的最小值是______ .
10.综合与实践
在△ABC中,BD⊥AC于点D,点P为射线BD上任一点(点B除外),连接AP,将线段PA绕点P顺时针方向旋转α,α=∠ABC,得到PE,连接CE.
(1)如图1,当BA=BC,且∠ABC=60°时,BP与CE的数量关系是 ,BC与CE的位置关系是
(2)如图2,当BA=BC,且∠ABC=90°时,(1)中的结论是否成立?若成立,请予以证明;若不成立,请说明理由.(请选择图2,图3中的一种情况予以证明或说理)
(3)在(2)的条件下,若AB=8,AP=,请直接写出CE的长.
11.(1)[问题发现]
如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为BC的中点,以CD为一条边作正方形CDEP,点E恰好与点A重合.则线段BE与AF的数量关系为______ ;
(2)[拓展研究]
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请就图2的情形给出证明;
(3)[问题发现]
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
12.如图1,在Rt△ABC中,∠ACB=90°,CA=CB,点D为AB边上一动点,连接CD,并将CD绕点C逆时针旋转90°得到CE,连接BE、DE,点F为DE中点,连接BF.
(1)求证:△ACD△BCE;
(2)如图2所示,在点D的运动过程中,当时(n>1),分别延长AC、BF相交于G:
①当时,求CG与AB的数量关系;
②当=n时(n>1),= ______ .
(3)当点D运动时,在线段CD上存在一点M,使得AM+BM+CM的值最小,若CM=2,则BE= ______.
13.如图1,在中,∠B=90°,,,点分别是边的中点,连接.将△CDE绕点逆时针方向旋转,记旋转角为.
(1)问题发现
当时,______;当时,______.
(2)拓展探究
试判断:当时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点逆时针旋转至三点在同一条直线上时,请直接写出线段的长______.
14.(1)问题探究:如图1,在正方形,点,分别在边,上,于点,点,分别在边、上,.
①判断与的数量关系:______;
②推断:的值为:______ ;(无需证明)
(2)类比探究:如图(2),在矩形中,.将矩形沿折叠,使点落在边上的点处,得到四边形,交于点,连接交于点.试探究与之间的数量关系,并说明理由;
(3)拓展应用1:如图3,四边形中,,,,,点,分别在边、上,求的值.
(4)拓展应用2:如图2,在(2)的条件下,连接,若,,求的长.
15.【问题背景】
在四边形中,,,E、F分别是、上的点,且,试探究图1中线段、、之间的数量关系.
【初步探索】
小亮同学认为:延长到点G,使,连接,再证明,则可得到、、之间的数量关系是___________.
【探索延伸】
在四边形中如图2,,,E、F分别是、上的点,,上述结论是否仍然成立?
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角()为70°,试求此时两舰艇之间的距离.
参考答案:
1.解:(1)①∵△ABC和△AGF都是等腰直角三角形,∠BAC=∠G=90°,
∴∠B=∠C=∠GAF=45°,
又∵∠AED=∠NEA,
∴△ABE∽△DAE,
∴,
∴;
②∵∠DAC=∠DAE+∠CAE,∠AEB=∠C+∠CAE,∠C=∠DAE=45°,
∴∠AEB=∠DAC,
又∵∠B=∠C,
∴△AEB∽△DAC,
∴,
∴,
∵AB=AC,∠BAC=90°,BC=6,
∴,即,
∴,
∴;
(2)∵,
∴可设,,
∵∠B=∠DAE=30°,∠ADE=∠BDA,
∴△ADE∽△BDA,
∴,
∴,
可设,,
∴,
∵∠B=30°,∠ACB=90°,
∴,
∴,
∴
在直角△ACD中,,
∴,
∴,
∴.
2.(1),理由如下:
∵四边形ABCD是矩形,,
∴四边形ABCD是正方形,
∴,,
∵,,
∴,,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴,
∴,
,
在和中,
,
∴,
∴,
故答案为,
(2)仍然成立,理由如下:
∵四边形ABCD是矩形,,,
∴
∴,
∵,
∴,
∴,
∴,
∴四边形ABCD是矩形,,
∴,
∴,
∴,
∵四边形ABCD是矩形,
∴,
∵,
∴,
∴,,
在和中,
,
∴,
∴,
(3)如图所示,延长FC交AD于R,
∵四边形ABCD是矩形,
∴,,,,
∵,,
∴,
∴,
分两种情况:
①当时,
∵,
∴,,
在中,由勾股定理得:
,
∵,,
∴,
∴,
由勾股定理得:EF=;
②当时,同理可得:,
,,
,
由勾股定理得:
,
综上所说,若射线FC过AD的三等分点,,,
则线段EF的长为或.
3.(1)证明:∵平分,
∴,
∵,,
∴,
∴,
∴,
∴,即DE平分;
(2)证明:∵,
∴,
∵,
∴,
∴,
由(1)知,
∴,
∴;
(3)解:如图3,在AB上取一点F使AF=AD,连接CF,
∵平分,
∴,
∵,
∴,
∴,,,
∵,
∴,
∵,
∴,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,即
4.(1)解:如图,连接AG,
由折叠性质得AG⊥EF,
∵EFBD,
∴AG⊥BD,
在矩形ABCD中,AB=8,BC=6,
∴∠DAB=90°,AD=BC=6,
∴DB==10,
∵△GEF是由△AEF沿直线EF对折而成,
∴△GEF≌△AEF,
∴EF为AG中垂线,
∵EFBD,
∴EF=BD=5;
(2)解:∵点D,G,E三点共线,
∴∠DGF=90°,
设AF=3t,则FG=3t,AE=4t,DF=6-3t,
在Rt△DFG中,,即=36-36t,
∵tan∠FDG=,
∴,∴t=,∴AE=;
(3)解:①当△AEF∽△GHE时,如图,过点H作HP⊥AB于P,
∵∠AEF=∠FEG=∠EHG,∠EHG+∠HEG=90°,
∴∠FEG+∠HEG=90°,
∴∠A=∠FEH=90°,
∴△AEF∽△EHF,
∴EF:HE=AF:AE=1:2,
∵∠A=∠HPE=90°,
∴∠AEF+∠HEP=90°,∠HEP+∠EHP=90°,
∴∠AEF=∠EHP,
∴△AEF∽△HPE,
∴AE:HP=EF:EH=1:2,
∴HP=6,
∴AE=3;
②当△AEF∽△GHE时,如图,过点H作HP⊥AB于P,
同理可得EF:HE=1:2,EA:HP=1:2,
设AF=t,则AE=2t,EP=2t,HP=4t,BP=8-4t,
∵△BHP∽△BDA,
∴4t:6=(8-4t):8,
∴t=,
∴AE=;
③当△AEF∽△GEH时,如图,过点G作MNAB交AD于点M,过点E作EN⊥MN于N,
设AF=t,则AE=2t,DF=6-t,
由折叠可知,△AEF≌△GEF,
∴AE=GE,
∵△AEF∽△GEH,AE=GE,
∴△AEF≌△GEH(AAS),
∴FG=GH,
∵MGDH,
∴FM=(6-t),
∴AN=EN=AF+FM=,
∵△FMG∽△GNE,GF:GE=1:2,
∴MG=NE=AM=,GH=2FN=6-t,
∵MN=AE,
∴+6-t=2t,
∴t=,
∴AE=;
④当△AEF∽△GEH时,如图,过点G作MNAB交AD于点M,过点E作EN⊥MN于N,过点H作HQ⊥AD于Q,
设AF=t,则AE=2t,
设FM=a,则NG=2a,NE=a+t,
∴MG=EN=AM=,
∴+2a=2t,
由上题知,MF=MQ=a,QH=2MG=a+t,
∴DQ=6-t-2a,
∵,
∴,
∴t=,
∴AE=.
综上,满足条件取线段AE的长为:3或或或.
5.(1)当AM=CM,即∠CAM=∠C=30°时,△AMC是等腰三角形;
∵∠BAC=90°,
∴α=90° 30°=60°,
当AM=CM,即∠CAM=∠CMA时,△AMC是等腰三角形,
∵∠C=30°,
∴∠CAM=∠AMC=75°,
∵∠BAC=90°,
∴α=15°,
综上所述,当旋转角α=60°或15°时,△AMC是等腰三角形,
故答案为:60°或15°;
(2)由题意可知,AB=AF,∠B=∠F,∠E=∠C,AE=AC,
∵现将Rt△AEF绕A点按逆时针方向旋转α(0°<α<90°),
∴∠BAM=∠FAN,
在△ABM与△AFN中,
,
∴,
∴AM=AN,
∵AE=AC,
∴EM=CN,
在和中
,
∴,
∴PE=PC,
∴点P在CE的垂直平分线上,
∵AE=AC,
∴点A在CE的垂直平分线上,
∴AP所在的直线是线段CE的垂直平分线;
(3)∵α=30°,∠B=60°,
∴∠AMB=90°,
∴△ABM是直角三角形,
∵AB=2,
∴BM=AB sin30°=1,AM=AB cos30°=,
∴=AM MB=1×=,
∵AE=AC=AB tan60°=2,AM=,
∴EM=,
在和中
∴,
由(2)可知,
∴=,
∵AF AE=×2×2=2,
∴△ABC与△AFE重叠的面积2 2×=;
(4)如答题图1所示:当∠CNP=90°时.
∵∠CNP=90°,
∴∠ANF=90°.
又∵∠AFN=60°,
∴∠FAN=180° 60° 90°=30°.
∴∠α=30°.
如答题图2所示:当∠CPN=90°时.
∵∠C=30°,∠CPN=90°,
∴∠CNP=60°.
∴∠ANF=60°.
又∵∠F=60°,
∴∠FAN=60°.
∴∠α=60°.
综上所述,∠α=30°或60°.
6.(1)解:∵和均为等边三角形,
∴,,
∴,
故答案为:;
(2)如图2中,
①∵和均为等边三角形,
∴,,,
∴,
∴(SAS),
∴;
②∵,
∴,
设交于点.
∵,
∴,
∴,
故答案为:;
(3)结论:,.
理由:如图3中,
∵,,,
∴,,
∴,
∴,,
∴,
∵,
∴.
7.(1)①∵AE是AD绕点A逆时针旋转60°而得到的
∴AD=AE,∠DAE=60°
∵△ABC是等边三角形
∴AB=AC=BC,∠B=∠BAC=60°
∴∠BAD+∠DAC=∠DAC+∠CAE=60°
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠ACE=∠B=60°
故答案为:60°
②由①知:△ABD≌△ACE
∴BD=CE
∴CA=BC=BD+CD=CE+CD
故答案为:CA=CE+CD
(2)理由如下:
∵AE是AD绕点A逆时针旋转90°而得到的
∴AD=AE,∠DAE=90°
∵AB=AC,
∴由勾股定理得:
∵
∴∠BAD+∠DAC=∠DAC+∠CAE=90°
∴∠BAD=∠CAE
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
∴BC=BD+CD=CE+CD
∴
(3)如图,在线段CD上取CE=BD,连接AE,设AB、CD交于点F
∵∠BAC=∠CAE=90°,∠BFD=∠CFA
∴∠DBA=∠ECA
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴AD=AE,∠DAB=∠EAC
∴∠DAE=∠DAB+∠BAE=∠EAC+∠BAE=∠BAC=90°
∴△ADE是等腰直角三角形
∴由勾股定理得:
∴
∵,
∴由勾股定理得:
∵BD=5,
∴在Rt△BDC中,由勾股定理得:CD=
∵
∴
解得:
8.解:(1)AM=AD+MC.理由如下:
如图1(1)所示,分别延长AE,BC交于点N,
∵四边形ABCD是正方形,
∴ADBC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
∵E是CD的中点,
∴DE=CE,
在ADE与NCE中,
∴ADE≌NCE(AAS),
∴AD=NC,
∵MN=NC+MC,
∴AM=AD+MC;
(2)AM=DE+BM成立.理由如下:
如图1(2)所示,将ADE绕点A顺时针旋转90°,得到ABF,
∵四边形ABCD是正方形,
∴ABDC,∠D=∠ABM=90°,
∴∠AED=∠BAE,
∵旋转,
∴∠F=∠AED,∠FAB=∠EAD,BF=ED,∠D=∠ABF=90°,
∴∠ABM+∠ABF=180°,
∴点F、B、M在同一直线上,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠BAF=∠MAE,
∵∠BAE=∠BAM+∠MAE,
∴∠AED=∠BAM+∠BAF=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∵FM=BF+BM
∴AM=DE+BM;
(3)①结论AM=AD+MC仍然成立,理由如下:
①如图2(1),延长、交于点,
四边形是矩形,
.
.
平分,
.
.
.
在ADE与PCE中,
;∴ADE≌PCE(AAS),
.
∵MP=PC+MC,
∴AM=AD+MC;
②结论不成立,理由如下:
假设成立.
过点作,交的延长线于点,如图2(2)所示.
四边形是矩形,
,.
,
.
.
.
,
.
,
,
.
.
.
,
.
,
与条件“ “矛盾,故假设不成立.
不成立.
9.解:(1)①∵边AB绕点B顺时针旋转得到线段,
∴,.
∵AC=BC=4,,
∴.
∴.
∴.
∵,
∴.
∴.
∴.
∴BD=AC=4.
∴CD=BC+BD=8.
故答案为:8.
②∵,
∴.
∴.故答案为:8.
(2),证明如下:
∵边AB绕点B顺时针旋转得到线段,
∴,.
∴.
∵,
∴.
∴.
∵,
∴.
∴.
∴.
∴,BD=AC.
∴.
(3)如下图所示,过点作交CB延长线于点F,过点A作交CB于点E,交线段于点M,再连接DC.
①∵AB=AC=5,BC=6,且,
∴,.
∴.
∵边AB绕点B顺时针旋转得到线段,
∴,.
∴.
∴.
∵,
∴.
∴.
∴.
∴.
∴.
故答案为:9.
②∵,且BE=CE,
∴AE垂直平分CB.
∴DC=DB.
∴.
∵点D在AE上,
∴.
∴当点D与点M重合时,有最小值,此时最小值为.
∵,,
∴.
∵BC=6,
∴CF=BC+BF=10.
∴.
∴的最小值为.
故答案为:.
10.解:(1)BP=CE,BC⊥CE,理由如下:
如图所示,连接AE,
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=∠ABC=∠ACB=60°,
由旋转的性质得,PA=PB,,
∴△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∴∠BAP+∠PAD=∠CAE+∠APD,即∠BAP=∠CAE,
在△BAP和△CAE中,
,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE,
∵BD⊥AC,△ABC是等边三角形,
∴,
∴∠ACE=30°,
∴∠BCE=∠ACE+∠ACB=90°,
∴BC⊥CE;
故答案为:BP=CE,BC⊥CE;
(2)(1)中结论BC⊥CE仍然成立,BP=CE不成立,结论是,理由如下:
如图所示,连接AE,
∵AB=BC,∠ABC=90°,
∴,∠BAC=∠BCA=45°,
由旋转的性质得,PA=PB,,
∴,∠PAE=∠PEA=45°,
∴∠BAP+∠PAD=∠CAE+∠PAD,即∠BAP=∠CAE,
∵,
∴△BAP∽△CAE,
∴,∠ACE=∠ABP,
∴,
∵AB=BC,BD⊥AC,
∴,
∴∠ACE=45°,
∴∠BCE=∠ACE+∠ACB=90°,
∴BC⊥CE;
(3)如图2所示,当P在线段BD上时,
∵AB=BC=8,∠ABC=90°,
∴,∠BAD=45°,
∵BD⊥AC,
∴,,
∴∠ABD=∠BAD,
∴,
∵,
∴,
∴,
∴;
如图3所示,当P在BD延长线上时,连接AE,
同理可证∠BAC=∠PAE=45°,
∴∠BAD+∠PAD=∠PAE+∠PAD,即∠BAP=∠CAE,
同理可得,
∴△BAP∽△CAE,
∴,
∴,
同理可求得,,
∴,
.
∴综上所述,CE=2或14.
11.解:(1)在Rt△ABC中,AB=AC=4,
根据勾股定理得,BC=AB=4,
点D为BC的中点,
∴AD=BC=2,
∵四边形CDEF是正方形,
∴AF=EF=AD=2,
∵BE=AB=4,
∴BE=AF,
故答案为BE=AF;
(2)无变化;
如图2,在Rt△ABC中,AB=AC=4,
∴∠ABC=∠ACB=45°,
∴sin∠ABC==,
在正方形CDEF中,∠FEC=∠FED=45°,
在Rt△CEF中,sin∠FEC==,
∴=,
∵∠FCE=∠ACB=45°,
∴∠FCE+∠ACE=∠ACB+∠ACE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴==,
∴BE=AF,
∴线段BE与AF的数量关系无变化;
(3)当点E在线段AF上时,
由(1)知,CF=EF=CD=2,
在Rt△BCF中,CF=2,BC=4,
根据勾股定理得,BF=2,
∴BE=BF﹣EF=2﹣2,
由(2)知,BE=AF,
∴AF=2﹣2,
当点E在线段BF的延长线上时,如图3,
在Rt△ABC中,AB=AC=4,
∴∠ABC=∠ACB=45°,
∴sin∠ABC==,
在正方形CDEF中,∠FEC=∠FED=45°,
在Rt△CEF中,sin∠FEC==,
∴=,
∵∠FCE=∠ACB=45°,
∴∠FCB+∠ACB=∠FCB+∠FCE,
∴∠FCA=∠ECB,
∴△ACF∽△BCE,
∴==,
∴BE=AF,
由(1)知,CF=EF=CD=2,
在Rt△BCF中,CF=2,BC=4,
根据勾股定理得,BF=2,
∴BE=BF+EF=2+2,
由(2)知,BE=AF,
∴AF=2+2.
即:当正方形CDEF旋转到B,E,F三点共线时候,线段AF的长为2﹣2或2+2.
12.(1)证明:∵把CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=∠DCB+∠ECB=90°.
又∵∠ACB=90°=∠ACD+∠DCB,
∴∠ACD=∠ECB,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS);
(2)①∵∠ACB=90°,CA=CB,
∴∠A=∠CBA=45°,
∵△ACD≌△BCE,
∴∠A=∠CBE=45°,
∴∠DBE=90°,
∵=,
过点G作GH⊥AB,
∵点F为DE中点,
∴DF=FB=,
∴∠FDB=∠FBD,
∴tan∠FDB=tan∠FBD,
∴,
∵∠A=45°,
∴是等腰直角三角形,
∴GH=AH,
∴,此时,H、D重合,
∴设AD=3x,BD=2x,则AB=5x,AC=BC=5x÷=,
∴GH=AH=3x,AG=3x
∴CG=3x-=,
∴
②当=n时(n>1),
设AD=nx,BD=x,则AB=(n+1)x,AC=BC=(n+1)x÷=,
同理:GH=AH=nx,AG=nx
∴CG=nx-=,
∴=,
故答案是:;
(3)如图,把绕点A顺时针旋转60°,得到,
∴AM=AG,BM=HG,∠MAG=60°,
∴是等边三角形,
∴MA=MG,
∴AM+BM+CM= HG+MG+CM,当点C、M、G、H四点共线时,AM+BM+CM的值最小,
连接BH,
∵把绕点A顺时针旋转60°,得到,
∴AM=AG,AB=AH,∠MAG=60°,
∴是等边三角形,是等边三角形,
∴∠AMG=∠AGM=60°,AH=BH,
∵AC=BC,
∴CH垂直平分AB,即CD垂直平分AB,
∴∠MAD=30°,
设AD=a,则MD=,
∵CM=2,AD=CD,
∴+2=a,解得:a=3+,
∴BE=AD=3+.
故答案是:3+.
13.(1)解:当时,
Rt中,∠B=90°,
,
点分别是边的中点,
,,
,
故答案为:;
如图,
当时,可得,
,
,
故答案为:;
(2)解:如图,
当时,的大小没有变化,
,
,
,
,
;
(3)解:如图,当点在的延长线上时,
在Rt中,,,
,
,
,
;
如图,当点在线段上时,
在Rt中,,,
,
,
,
,
综上所述,满足条件的的长为或.
14.解:(1)①证明:四边形是正方形,
,.
.
,
.
.
,
.
故答案为:.
②结论:.
理由:,,
,
,
四边形是平行四边形,
,
,
,
.
故答案为:1.
(2)结论:.
理由:如图2中,过点作于.
,
,
,,
,
,
,
,
四边形是矩形,
,
.
(3)如图3,过点作,交的延长线于点,过点作,连接,
,,,
四边形是矩形,
,,,
,,,
,
,
,且,
,且,
,
,
,,
,
,
(不合题意,舍去),,
,
由(2)的结论可知:.
(4)解:如图2中,过点作交的延长线于.
,
假设,,,
,,
,
,
或(舍弃),
,,
,
,
,,
,
,,
,
,
,
,
,,
,
.
15.证明:(初步探索)如图1,延长到点G,使,连接,
在和中
,
在和中
∴,
∵,
∴;
(探索延伸)证明:如图,延长到点G,使,连接,
则:,
∵,
∴,
在和中
;∴(SAS),
∴,
∵,
∴,
∴,即:,
在和中
;∴(SAS),
∴,
∵,
∴;
(结论运用)解:连接,延长、相交于点,
,
又,
∴图形符合探索延伸中的条件,
∴结论,成立,
∵,
∴(海里);
∴两舰艇之间的距离为:210海里.
同课章节目录
