【中考数学几何模型】第十八节:三角形相似388-395(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十八节:三角形相似388-395(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 336.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:36:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十八节:三角形相似
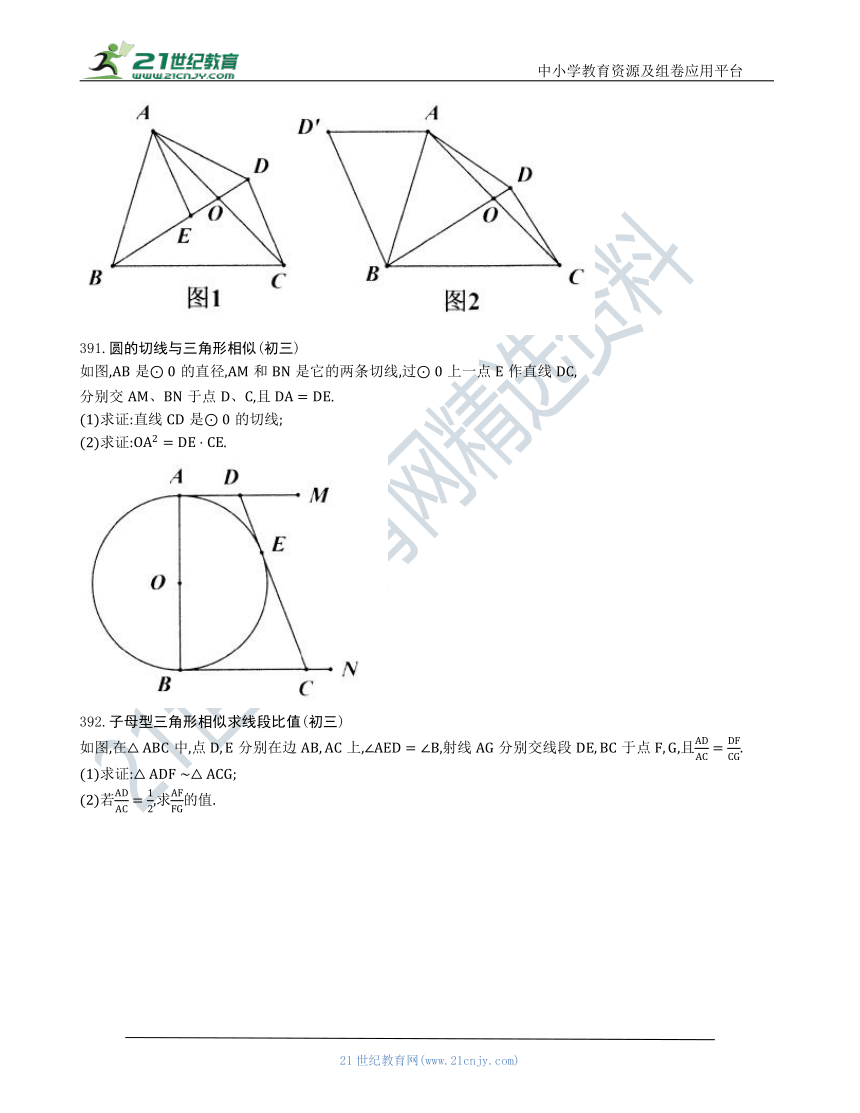
388.三角形相似动点求最大值(初三)
如图,在四边形中,为边上一点(不与重合),连接,过点作交于,使得.
(1)与相似吗 为什么
(2)若,求的长;
(3)当为多少时,的长最大 最大为多少
389.倍长中线三角形全等三角形相似综合题(初三)
如图,等腰中,为的中点,延长至,使与交于点
(1)求的值;
(2)求证:
(3)如果,直接写出CM的长
390.翻折等腰与三角形相似(初三)
如图1,四边形的对角线相交于点.
(1)过点作交于点,求证:;
(2)如图2,将沿翻折得到
①求证:
②若,求证:.
391.圆的切线与三角形相似(初三)
如图,是的直径,和是它的两条切线,过上一点作直线,
分别交于点,且.
(1)求证:直线是的切线;
(2)求证:.
392.子母型三角形相似求线段比值(初三)
如图,在中,点分别在边上,,射线分别交线段于点,且.
(1)求证:;
(2)若,求的值.
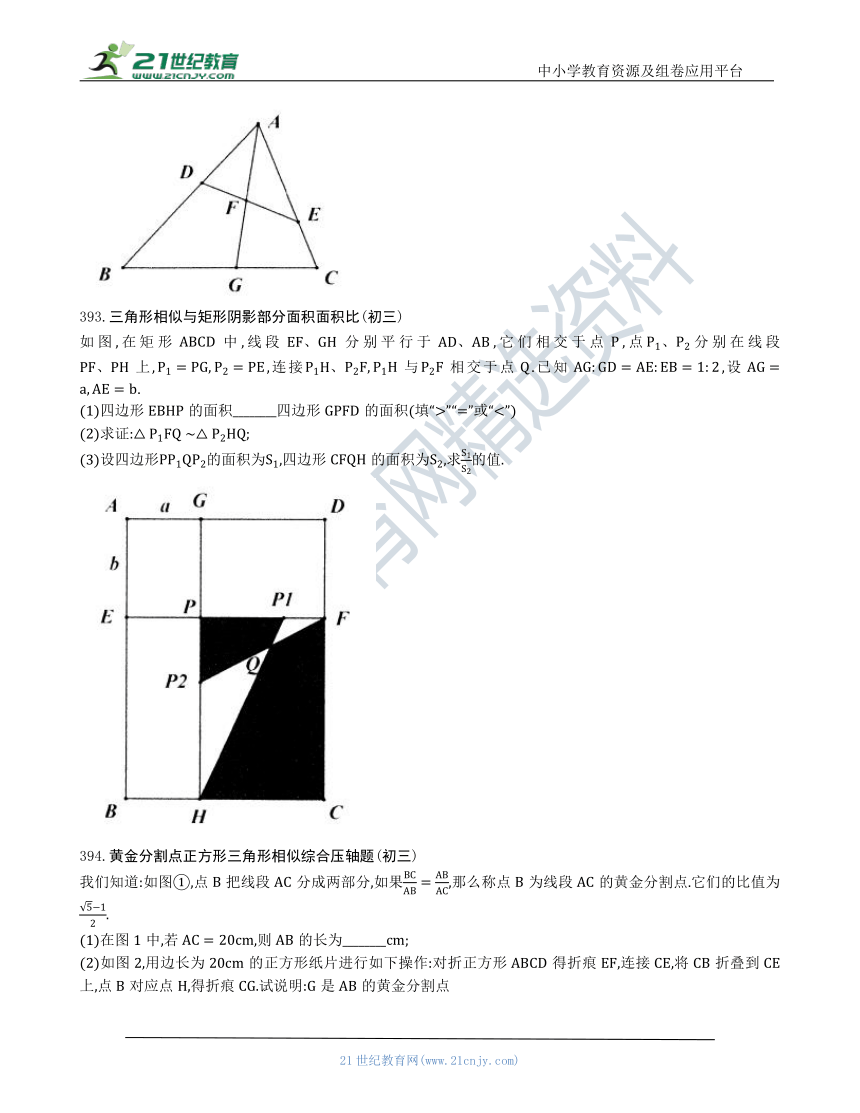
393.三角形相似与矩形阴影部分面积面积比(初三)
如图,在矩形中,线段分别平行于,它们相交于点,点分别在线段上,,连接与相交于点.已知,设.
(1)四边形EBHP的面积________四边形GPFD的面积(填“”“=”或“”)
(2)求证:;
(3)设四边形的面积为,四边形的面积为,求的值.
394.黄金分割点正方形三角形相似综合压轴题(初三)
我们知道:如图①,点把线段分成两部分,如果,那么称点为线段的黄金分割点.它们的比值为.
(1)在图1中,若,则的长为________;
(2)如图2,用边长为的正方形纸片进行如下操作:对折正方形得折痕,连接,将折叠到上,点对应点,得折痕.试说明:是的黄金分割点
(3)如图3,小明进一步探究:在边长为的正方形的边上任取点,连接,作,交于点,延长交于点.他发现当与满足某种关系时,恰好分别是的黄金分割点.请猜想小明的发现,并说明理由
395.旋转型三角形相似探究与拓展延伸(初三)
问题背景:如图1,在矩形中,,点是边的中点,过点作交于点.实验探究:
(1)在一次数学活动中,小王同学将图1中的,绕点按逆时针方向,旋转,如图2所示,得到结论:①________②直线与所夹锐角的度数为________
(2)小王同学继续将绕点按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立 并说明理由.
拓展延伸:
在以上探究中,当旋转至三点共线时,则的面积为________
答案
388.【解】(1))与相似;理由如下:
,
,
;
(2)由(1)可知:,
,
,解得:;
(3)设,则,
由(1)可知,
,
当时,有最大值,
当为时,的长最大,最大为.
389.【解】(1)如图1,作交延长线于,
图1图2
(2)如图2,延长至,使,连接,
在与中,
,
,设,则,
,
,
,
,
,
;
(3),
,设,
由.
390.解(1)证明:,,又,
,
;
(2)(1)证明:如图1,过点作交于点,
由(1)可知,
,
将沿翻折得到,
,
又.
图1图2
(2)证明:如图2,过点作交于点,延长交于点,由翻折可知,
,
,
,
,
,由(1)知,
.
391.【解】(1)连接,如图1,
在和中,,
,
是的切线,
,
直线是的切线;
(2)过作于点,如图2,
则都是的切线,
,
四边形是矩形,,
是的切线,,
,
,
即.
图1图2
392.(1)证明:,
.
(2)【解】,
又.
393.【解】(1)四边形为矩形,
,
,
,
四边形为矩形,
同理可得,四边形均为矩形,
,
,
四边形的面积,四边形
的面积,故答案为:;
(2),
由(1)知,,即,
又,
,
;
(3)连接,
,
,
,由(2)中,
得,
,
,
,
.
394.【解】(1)点为线段的黄金分割点,
.
故答案为:.
(2)延长交于点四边形为正方形,
,由折叠的性质可知,
,
,
,
,
.
,即,
是的黄金分割点;
(3)当时,满足题意.理由如下:
四边形是正方形,
,
,又,
,
,
,当恰好分别是的黄金分
割点时,,
.
395.【解】(1)如图1,,
,
如图2,设与交于点与交于点,
绕点按逆时针方向旋转,
,又,
直线与所夹锐角
的度数为,故答案为:;
(2)结论仍然成立,理由如下:
如图3,设与交于点与交于点,
将绕点按逆时针方向旋转,
,又,
,
,又,
,
直线与所夹锐角的度数为.
拓展延伸:如图4,当点在的上方时,过点作于,点是边的中点,,
,
三点共线,,
,
,由(2)可得:,
的面积;
如图5,当点在的下方时,过点作,交的延长线于,同理可求:的面积;故答案为:或.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十八节:三角形相似
388.三角形相似动点求最大值(初三)
如图,在四边形中,为边上一点(不与重合),连接,过点作交于,使得.
(1)与相似吗 为什么
(2)若,求的长;
(3)当为多少时,的长最大 最大为多少
389.倍长中线三角形全等三角形相似综合题(初三)
如图,等腰中,为的中点,延长至,使与交于点
(1)求的值;
(2)求证:
(3)如果,直接写出CM的长
390.翻折等腰与三角形相似(初三)
如图1,四边形的对角线相交于点.
(1)过点作交于点,求证:;
(2)如图2,将沿翻折得到
①求证:
②若,求证:.
391.圆的切线与三角形相似(初三)
如图,是的直径,和是它的两条切线,过上一点作直线,
分别交于点,且.
(1)求证:直线是的切线;
(2)求证:.
392.子母型三角形相似求线段比值(初三)
如图,在中,点分别在边上,,射线分别交线段于点,且.
(1)求证:;
(2)若,求的值.
393.三角形相似与矩形阴影部分面积面积比(初三)
如图,在矩形中,线段分别平行于,它们相交于点,点分别在线段上,,连接与相交于点.已知,设.
(1)四边形EBHP的面积________四边形GPFD的面积(填“”“=”或“”)
(2)求证:;
(3)设四边形的面积为,四边形的面积为,求的值.
394.黄金分割点正方形三角形相似综合压轴题(初三)
我们知道:如图①,点把线段分成两部分,如果,那么称点为线段的黄金分割点.它们的比值为.
(1)在图1中,若,则的长为________;
(2)如图2,用边长为的正方形纸片进行如下操作:对折正方形得折痕,连接,将折叠到上,点对应点,得折痕.试说明:是的黄金分割点
(3)如图3,小明进一步探究:在边长为的正方形的边上任取点,连接,作,交于点,延长交于点.他发现当与满足某种关系时,恰好分别是的黄金分割点.请猜想小明的发现,并说明理由
395.旋转型三角形相似探究与拓展延伸(初三)
问题背景:如图1,在矩形中,,点是边的中点,过点作交于点.实验探究:
(1)在一次数学活动中,小王同学将图1中的,绕点按逆时针方向,旋转,如图2所示,得到结论:①________②直线与所夹锐角的度数为________
(2)小王同学继续将绕点按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立 并说明理由.
拓展延伸:
在以上探究中,当旋转至三点共线时,则的面积为________
答案
388.【解】(1))与相似;理由如下:
,
,
;
(2)由(1)可知:,
,
,解得:;
(3)设,则,
由(1)可知,
,
当时,有最大值,
当为时,的长最大,最大为.
389.【解】(1)如图1,作交延长线于,
图1图2
(2)如图2,延长至,使,连接,
在与中,
,
,设,则,
,
,
,
,
,
;
(3),
,设,
由.
390.解(1)证明:,,又,
,
;
(2)(1)证明:如图1,过点作交于点,
由(1)可知,
,
将沿翻折得到,
,
又.
图1图2
(2)证明:如图2,过点作交于点,延长交于点,由翻折可知,
,
,
,
,
,由(1)知,
.
391.【解】(1)连接,如图1,
在和中,,
,
是的切线,
,
直线是的切线;
(2)过作于点,如图2,
则都是的切线,
,
四边形是矩形,,
是的切线,,
,
,
即.
图1图2
392.(1)证明:,
.
(2)【解】,
又.
393.【解】(1)四边形为矩形,
,
,
,
四边形为矩形,
同理可得,四边形均为矩形,
,
,
四边形的面积,四边形
的面积,故答案为:;
(2),
由(1)知,,即,
又,
,
;
(3)连接,
,
,
,由(2)中,
得,
,
,
,
.
394.【解】(1)点为线段的黄金分割点,
.
故答案为:.
(2)延长交于点四边形为正方形,
,由折叠的性质可知,
,
,
,
,
.
,即,
是的黄金分割点;
(3)当时,满足题意.理由如下:
四边形是正方形,
,
,又,
,
,
,当恰好分别是的黄金分
割点时,,
.
395.【解】(1)如图1,,
,
如图2,设与交于点与交于点,
绕点按逆时针方向旋转,
,又,
直线与所夹锐角
的度数为,故答案为:;
(2)结论仍然成立,理由如下:
如图3,设与交于点与交于点,
将绕点按逆时针方向旋转,
,又,
,
,又,
,
直线与所夹锐角的度数为.
拓展延伸:如图4,当点在的上方时,过点作于,点是边的中点,,
,
三点共线,,
,
,由(2)可得:,
的面积;
如图5,当点在的下方时,过点作,交的延长线于,同理可求:的面积;故答案为:或.
21世纪教育网(www.21cnjy.com)
同课章节目录
