【中考数学几何模型】第十六节:平面直角坐标系中动点找规律307-315(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十六节:平面直角坐标系中动点找规律307-315(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 11:38:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十六节:平面直角坐标系中动点找规律
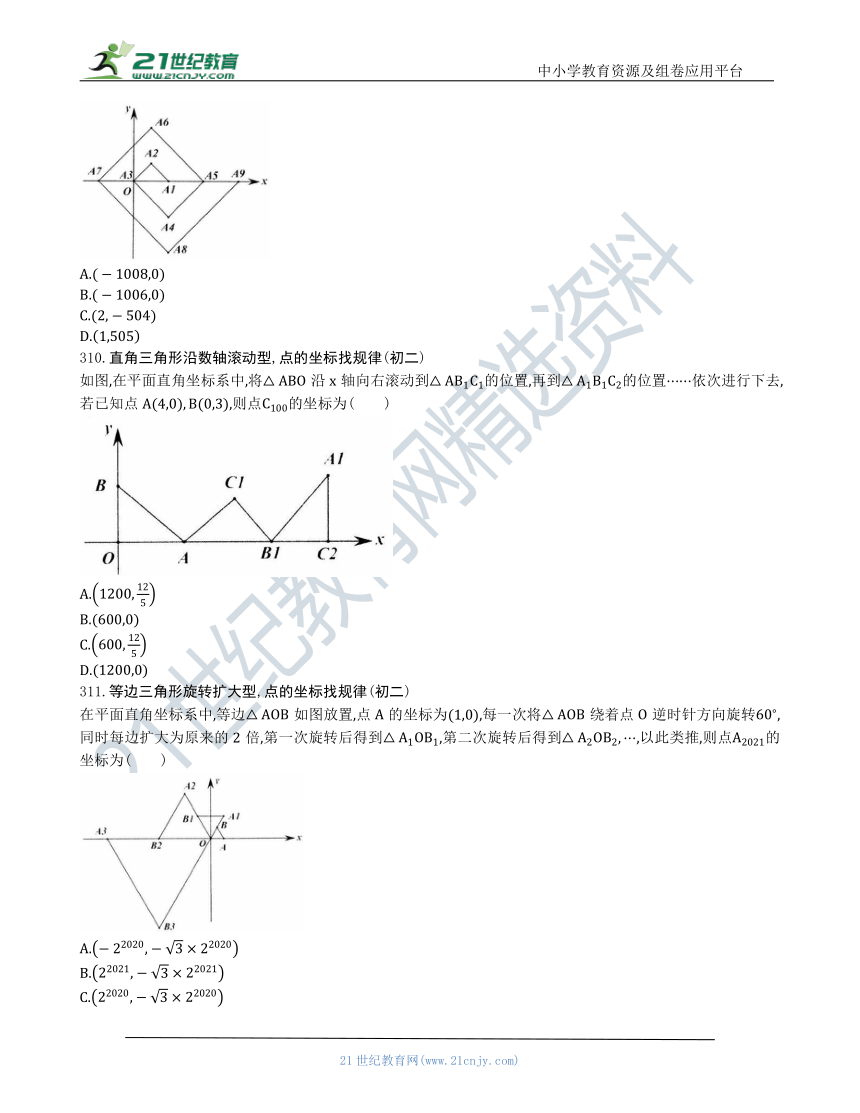
307.正多边形旋转型,点的坐标找规律(初二)
如图,边长为1的正六边形放置于平面直角坐标系中,边在轴正半轴上,顶点在y轴正半轴上,将正六边形绕坐标原点顺时针旋转,每次旋转,那么经过第2025次旋转后,顶点的坐标为( )
A.
B.
C.
D.
308.点的转圈爬行型,点的坐标找规律(初二)
如图,在平面直角坐标系中,1),一只瓢虫从点出发以2个单位长度/秒的速度沿循环爬行,问第2021秒瓢虫在( )处.
A.
B.
C.
D.
309.等腰直角三角形螺旋型,点的坐标找规律(初二)
如图,在单位为1的方格纸上,,都是斜边在x轴上,斜边长分别为的等腰直角三角形,若的顶点坐标分别为,则依图中所示规律,的坐标为( )
A.
B.
C.
D.
310.直角三角形沿数轴滚动型,点的坐标找规律(初二)
如图,在平面直角坐标系中,将沿轴向右滚动到的位置,再到的位置依次进行下去,若已知点,则点的坐标为( )
A.
B.
C.
D.
311.等边三角形旋转扩大型,点的坐标找规律(初二)
在平面直角坐标系中,等边如图放置,点的坐标为,每一次将绕着点逆时针方向旋转,同时每边扩大为原来的2倍,第一次旋转后得到,第二次旋转后得到,以此类推,则点的坐标为( )
A.
B.
C.
D.
312.一次函数交点型,点的坐标找规律(初二)
如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为( )
A.
B.
C.
D.
313.正方形旋转扩大型,点的坐标找规律(初二)
如图,点是正方形的两个顶点,以对角线为边作正方形,再以正方形的对角线作正方形,依此规律,则点的坐标是( )
A.
B.
C.
D.
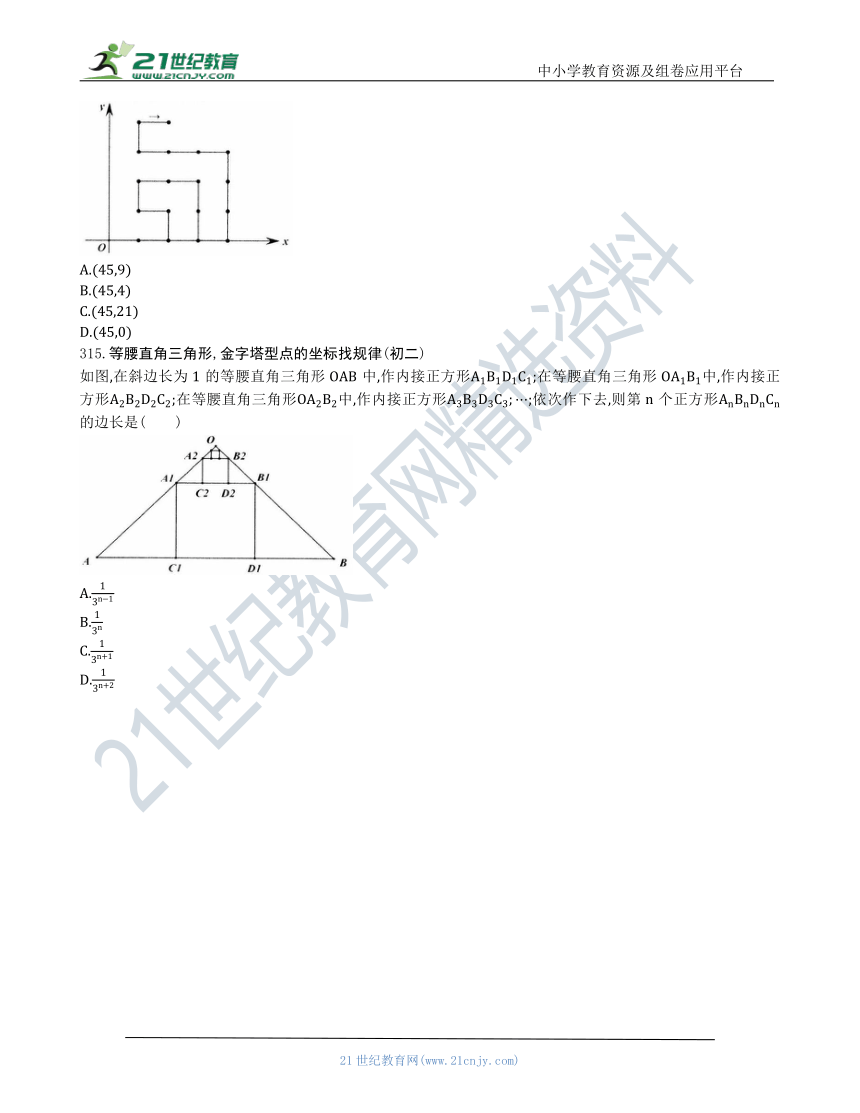
314.贪吃蛇型,点的坐标找规律(初一)
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,根据这个规律,第2021个点的坐标为( )
A.
B.
C.
D.
315.等腰直角三角形,金字塔型点的坐标找规律(初二)
如图,在斜边长为1的等腰直角三角形中,作内接正方形;在等腰直角三角形中,作内接正方形;在等腰直角三角形中,作内接正方形;依次作下去,则第个正方形的边长是( )
A.
B.
C.
D.
答案
307.【解】如图,连接.在正六边形中,.在Rt中,,
将正六边形绕坐标原点顺时针旋转,每次旋转次一个循环,经过第2025次旋转后,顶点的坐标与第三次旋转得到的的坐标相同.与关于原点对称,经过第2025次旋转后,顶点的坐标,故选:.
308.【解】
当秒时,瓢虫在点处,此时瓢虫的坐标为.故选:.
309.【解】观察图形可以看出每4个为一组,在轴负半轴上,纵坐标为0.、、的横坐标分别为的横坐标为的坐标为,故选:.
310.【解】根据题意,可知:每滚动3次为一个周期,点在第一象限,点在轴上.点的横坐标为,同理,可得出:点的横坐标为,点的横坐标为点的横坐标为为正整数点的横坐标为点的坐标为.故选:.
311.【解】由已知可得:
第一次旋转后,在第一象限,,
第二次旋转后,在第二象限,,
第三次旋转后,在轴负半轴,,
第四次旋转后,在第三象限,,
第五次旋转后,在第四象限,,
第六次旋转后,在轴正半轴,,
如此循环,每旋转6次,的对应点又回到轴正半轴,而在第四象限,且,故选:.
312.【解】联立直线与直线的表达式并解得:,故;
则点,则直线的表达式为:,将点坐标代入上式并解得:直线的表达式为:,将表达式与直线的表达式联立并解得:,即点的纵坐标为;
同理可得的纵坐标为按此规律,则点的纵坐标为,故选:.
313.【解】根据题意和图形可看出每经过一次变化,都顺时针旋转,边长都乘以.
从到经过了3次变化,点所在的正方形的边长为,点位置在第四象限,点的坐标是;
可得出:点坐标为点坐标为点坐标为点坐标为点坐标为,故选:.
314.【解】观察图形可知,到每一个横坐标结束,经过整数点的个数等于最后横坐标的平方,横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,横坐标为偶数时以横坐标为1,纵坐标以横坐标减1结束,横坐标以结束的有个点,第2025个点是个点的坐标是;故选:.
315.【解】法1:过作,交于点,交于点,如图所示:
∥.
为斜边为1的等腰直角二角形,.又为等腰直角三角形,第1个正方形的边长,同理第2个正方形的边长,则第个正方形的边长;
法2:由题意得:
,同理可得:,依此类推.故选:.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十六节:平面直角坐标系中动点找规律
307.正多边形旋转型,点的坐标找规律(初二)
如图,边长为1的正六边形放置于平面直角坐标系中,边在轴正半轴上,顶点在y轴正半轴上,将正六边形绕坐标原点顺时针旋转,每次旋转,那么经过第2025次旋转后,顶点的坐标为( )
A.
B.
C.
D.
308.点的转圈爬行型,点的坐标找规律(初二)
如图,在平面直角坐标系中,1),一只瓢虫从点出发以2个单位长度/秒的速度沿循环爬行,问第2021秒瓢虫在( )处.
A.
B.
C.
D.
309.等腰直角三角形螺旋型,点的坐标找规律(初二)
如图,在单位为1的方格纸上,,都是斜边在x轴上,斜边长分别为的等腰直角三角形,若的顶点坐标分别为,则依图中所示规律,的坐标为( )
A.
B.
C.
D.
310.直角三角形沿数轴滚动型,点的坐标找规律(初二)
如图,在平面直角坐标系中,将沿轴向右滚动到的位置,再到的位置依次进行下去,若已知点,则点的坐标为( )
A.
B.
C.
D.
311.等边三角形旋转扩大型,点的坐标找规律(初二)
在平面直角坐标系中,等边如图放置,点的坐标为,每一次将绕着点逆时针方向旋转,同时每边扩大为原来的2倍,第一次旋转后得到,第二次旋转后得到,以此类推,则点的坐标为( )
A.
B.
C.
D.
312.一次函数交点型,点的坐标找规律(初二)
如图,在平面直角坐标系中,直线与直线交于点,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为,过作的平行线交于,过作轴的垂线,垂足为按此规律,则点的纵坐标为( )
A.
B.
C.
D.
313.正方形旋转扩大型,点的坐标找规律(初二)
如图,点是正方形的两个顶点,以对角线为边作正方形,再以正方形的对角线作正方形,依此规律,则点的坐标是( )
A.
B.
C.
D.
314.贪吃蛇型,点的坐标找规律(初一)
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,根据这个规律,第2021个点的坐标为( )
A.
B.
C.
D.
315.等腰直角三角形,金字塔型点的坐标找规律(初二)
如图,在斜边长为1的等腰直角三角形中,作内接正方形;在等腰直角三角形中,作内接正方形;在等腰直角三角形中,作内接正方形;依次作下去,则第个正方形的边长是( )
A.
B.
C.
D.
答案
307.【解】如图,连接.在正六边形中,.在Rt中,,
将正六边形绕坐标原点顺时针旋转,每次旋转次一个循环,经过第2025次旋转后,顶点的坐标与第三次旋转得到的的坐标相同.与关于原点对称,经过第2025次旋转后,顶点的坐标,故选:.
308.【解】
当秒时,瓢虫在点处,此时瓢虫的坐标为.故选:.
309.【解】观察图形可以看出每4个为一组,在轴负半轴上,纵坐标为0.、、的横坐标分别为的横坐标为的坐标为,故选:.
310.【解】根据题意,可知:每滚动3次为一个周期,点在第一象限,点在轴上.点的横坐标为,同理,可得出:点的横坐标为,点的横坐标为点的横坐标为为正整数点的横坐标为点的坐标为.故选:.
311.【解】由已知可得:
第一次旋转后,在第一象限,,
第二次旋转后,在第二象限,,
第三次旋转后,在轴负半轴,,
第四次旋转后,在第三象限,,
第五次旋转后,在第四象限,,
第六次旋转后,在轴正半轴,,
如此循环,每旋转6次,的对应点又回到轴正半轴,而在第四象限,且,故选:.
312.【解】联立直线与直线的表达式并解得:,故;
则点,则直线的表达式为:,将点坐标代入上式并解得:直线的表达式为:,将表达式与直线的表达式联立并解得:,即点的纵坐标为;
同理可得的纵坐标为按此规律,则点的纵坐标为,故选:.
313.【解】根据题意和图形可看出每经过一次变化,都顺时针旋转,边长都乘以.
从到经过了3次变化,点所在的正方形的边长为,点位置在第四象限,点的坐标是;
可得出:点坐标为点坐标为点坐标为点坐标为点坐标为,故选:.
314.【解】观察图形可知,到每一个横坐标结束,经过整数点的个数等于最后横坐标的平方,横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,横坐标为偶数时以横坐标为1,纵坐标以横坐标减1结束,横坐标以结束的有个点,第2025个点是个点的坐标是;故选:.
315.【解】法1:过作,交于点,交于点,如图所示:
∥.
为斜边为1的等腰直角二角形,.又为等腰直角三角形,第1个正方形的边长,同理第2个正方形的边长,则第个正方形的边长;
法2:由题意得:
,同理可得:,依此类推.故选:.
21世纪教育网(www.21cnjy.com)
同课章节目录
