【中考数学几何模型】第十七节:反比例函数334-341(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十七节:反比例函数334-341(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 447.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 16:59:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十七节:反比例函数
334.反比函数值的几何意义求取值范围(初三)
如图,点在反比例函数的图象上,点在轴的正半轴上,点在轴的负半轴上,且.点是线段上一动点,过点和分别作轴的垂线,垂足为点和,连接.当时,的取值范围是_______.
335.反比函数值的几何意义(初三)
如图,过反比例函数图象上的四点分别作轴的垂线,垂足分别为,再过分别作y轴,,的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为,则与的数量关系为________.
336.反比例函数将军饮马最小值矩形存在性问题(初三)
如图,直线与双曲线交于两点,点的坐标为3),点是双曲线第一象限分支上的一点,连接并延长交轴于点,且
(1)求的值并直接写出点的坐标;
(2)点是轴上的动点,连接,求的最小值;
(3)是坐标轴上的点,是平面内一点,是否存在点,使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.
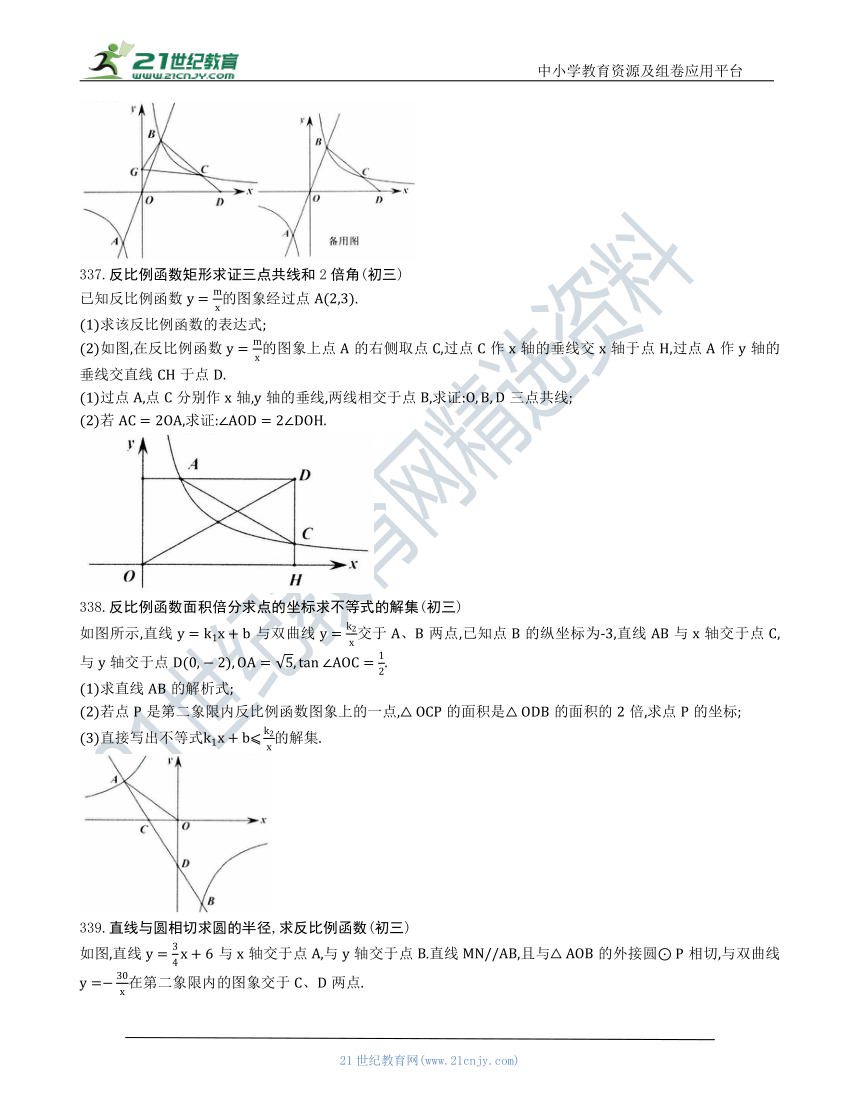
337.反比例函数矩形求证三点共线和2倍角(初三)
已知反比例函数的图象经过点.
(1)求该反比例函数的表达式;
(2)如图,在反比例函数的图象上点的右侧取点,过点作轴的垂线交轴于点,过点作轴的垂线交直线于点.
(1)过点,点分别作轴,轴的垂线,两线相交于点,求证:三点共线;
(2)若,求证:.
338.反比例函数面积倍分求点的坐标求不等式的解集(初三)
如图所示,直线与双曲线交于两点,已知点的纵坐标为-3,直线与轴交于点,与轴交于点.
(1)求直线的解析式;
(2)若点是第二象限内反比例函数图象上的一点,的面积是的面积的2倍,求点的坐标;
(3)直接写出不等式的解集.
339.直线与圆相切求圆的半径,求反比例函数(初三)
如图,直线与轴交于点,与轴交于点.直线,且与的外接圆相切,与双曲线在第二象限内的图象交于两点.
(1)求点的坐标和的半径;
(2)求直线所对应的函数表达式;
(3)求的面积.
340.反比例函数和一次函数综合题(初三)
如图,一次函数与反比例函数的图象交于点和,与轴交于点.
(1)求一次函数和反比例函数的解析式;
(2)在轴上取一点,当的面积为3时,求点的坐标;
(3)将直线向下平移2个单位后得到直线,当函数值时,求的取值范围.
341.反比例函数和正方形综合题(初三)
如图,已知边长为4的正方形中,轴,垂足为点轴,垂足为点,点在双曲线上,且点的横坐标为1.
(1)请求出两点的坐标;
(2)线段交于点,求出点到轴的距离;
(3)在双曲线上任取一点,连接,是否存在这样的点,使的面积等于5,若存在,请直接写出适合的所有的点坐标;若不存在,请说明理由.
答案
334.【解】过点作于,连接,过点作于点,连接,如图,
点在反比例函数的图象上,
从图中可以看出当点在线段上时,,即当点在线段上时,满足
设直线的解析式为,则:,解得:直线的解析式为,
解得:的取值范围为.
335.【解】过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积是个定值,.故答案为:.
336.【解】(1)将点的坐标为代入直线中,得,解得:反比例函数解析式为,由,解得或点的坐标为;
(2)如图1,作轴于点轴于点∥
,.
作点关于轴的对称点,连接交轴于点,则即为的最小值.
(3)存在.理由如下:
①当点在轴上时,如图2,设点的坐标为,0),过点作轴于点.
Rt中,勾股定理得:,
点的坐标为;
②当点在轴上时,过点作轴于点,如图2,设点的坐标为.
,即点的坐标为;
综上所述,点的坐标为或.
337.(1)【解】反比例函数的图象经过点(2,3),反比例函数的解析式为.
(2)证明:①过点作轴于,过点作轴于交于点,连接
,点在的图象上,可以设,则
共线.
②设交于轴,轴,∥轴,轴,∥四边形是平行四边形,四边形是矩形,.
.
∥.
338.【解】(1)如图1,过点作轴于,.
在Rt中,.设,则,根据勾股定理得,或(舍),.
点在双曲线上,双曲线的解析式为.
点在双曲线上,且纵坐标为.
将点代入直线中得,
直线的解析式为;
(2)如图2,连接,由(1)知,.
的面积是的面积的2倍,,由(1)知,直线的解析式为.令,则.
设点的纵坐标为.
由(1)知,双曲线的解析式为.
点在双曲线上,,2);
(4)由(1)知,,由图象知,不等式的解集为:或.
339.【解】(1)对于.令,解得.令,则,故点、的坐标分别为为直角,则是圆的直径,由点、的坐标得:,故圆的半径;
(2)过点作于点.设直线与圆切于点,连接,则,
则,
在Rt中,,即直线向上平移个单位得到,
故的表达式为;
(3)由直线的表达式知,点,联立的表达式和反比例函数表达式并整理得:,解得:或,故点的坐标为,由点、的坐标,坐标公式得:,则的面积.
340.【解】(1)过点,即反比例函数:.
当时,,即.
过和,则,解得:.
(2)当时,代入中得,,即.
且或;
(3)如图,设与的图象交于两点,向下平移两个单位得,且,
,联立得:,解得:或
或.
341.【解】(1)对于①,当时,,故点,即,则,故点的坐标为,点的坐标为;
(2)由(1)知,点.设直线的表达式为,则,解得:,故直线的表达式为.设直线交轴于点,则点.
同理可得,直线的表达式为,联立、的表达式并解得:,故点的纵坐标为,则点到轴的距离为;
(3)存在,理由:由直线的表达式知,点,由点的坐标知,,则,由点、的坐标知,.
①当点在上方时(∥,如图,过点作直线∥交轴于点,过点作于点,则的面积,解得
∥,则,在Rt中,,解得,则,故点,则直线的表达式为 ②,联立①②并解得:或,故点的坐标为或;
②当点在下方时(∥),同理可得,点的坐标为.
综上所述,点的坐标为或或.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十七节:反比例函数
334.反比函数值的几何意义求取值范围(初三)
如图,点在反比例函数的图象上,点在轴的正半轴上,点在轴的负半轴上,且.点是线段上一动点,过点和分别作轴的垂线,垂足为点和,连接.当时,的取值范围是_______.
335.反比函数值的几何意义(初三)
如图,过反比例函数图象上的四点分别作轴的垂线,垂足分别为,再过分别作y轴,,的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为,则与的数量关系为________.
336.反比例函数将军饮马最小值矩形存在性问题(初三)
如图,直线与双曲线交于两点,点的坐标为3),点是双曲线第一象限分支上的一点,连接并延长交轴于点,且
(1)求的值并直接写出点的坐标;
(2)点是轴上的动点,连接,求的最小值;
(3)是坐标轴上的点,是平面内一点,是否存在点,使得四边形是矩形?若存在,请求出所有符合条件的点的坐标;若不存在,请说明理由.
337.反比例函数矩形求证三点共线和2倍角(初三)
已知反比例函数的图象经过点.
(1)求该反比例函数的表达式;
(2)如图,在反比例函数的图象上点的右侧取点,过点作轴的垂线交轴于点,过点作轴的垂线交直线于点.
(1)过点,点分别作轴,轴的垂线,两线相交于点,求证:三点共线;
(2)若,求证:.
338.反比例函数面积倍分求点的坐标求不等式的解集(初三)
如图所示,直线与双曲线交于两点,已知点的纵坐标为-3,直线与轴交于点,与轴交于点.
(1)求直线的解析式;
(2)若点是第二象限内反比例函数图象上的一点,的面积是的面积的2倍,求点的坐标;
(3)直接写出不等式的解集.
339.直线与圆相切求圆的半径,求反比例函数(初三)
如图,直线与轴交于点,与轴交于点.直线,且与的外接圆相切,与双曲线在第二象限内的图象交于两点.
(1)求点的坐标和的半径;
(2)求直线所对应的函数表达式;
(3)求的面积.
340.反比例函数和一次函数综合题(初三)
如图,一次函数与反比例函数的图象交于点和,与轴交于点.
(1)求一次函数和反比例函数的解析式;
(2)在轴上取一点,当的面积为3时,求点的坐标;
(3)将直线向下平移2个单位后得到直线,当函数值时,求的取值范围.
341.反比例函数和正方形综合题(初三)
如图,已知边长为4的正方形中,轴,垂足为点轴,垂足为点,点在双曲线上,且点的横坐标为1.
(1)请求出两点的坐标;
(2)线段交于点,求出点到轴的距离;
(3)在双曲线上任取一点,连接,是否存在这样的点,使的面积等于5,若存在,请直接写出适合的所有的点坐标;若不存在,请说明理由.
答案
334.【解】过点作于,连接,过点作于点,连接,如图,
点在反比例函数的图象上,
从图中可以看出当点在线段上时,,即当点在线段上时,满足
设直线的解析式为,则:,解得:直线的解析式为,
解得:的取值范围为.
335.【解】过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积是个定值,.故答案为:.
336.【解】(1)将点的坐标为代入直线中,得,解得:反比例函数解析式为,由,解得或点的坐标为;
(2)如图1,作轴于点轴于点∥
,.
作点关于轴的对称点,连接交轴于点,则即为的最小值.
(3)存在.理由如下:
①当点在轴上时,如图2,设点的坐标为,0),过点作轴于点.
Rt中,勾股定理得:,
点的坐标为;
②当点在轴上时,过点作轴于点,如图2,设点的坐标为.
,即点的坐标为;
综上所述,点的坐标为或.
337.(1)【解】反比例函数的图象经过点(2,3),反比例函数的解析式为.
(2)证明:①过点作轴于,过点作轴于交于点,连接
,点在的图象上,可以设,则
共线.
②设交于轴,轴,∥轴,轴,∥四边形是平行四边形,四边形是矩形,.
.
∥.
338.【解】(1)如图1,过点作轴于,.
在Rt中,.设,则,根据勾股定理得,或(舍),.
点在双曲线上,双曲线的解析式为.
点在双曲线上,且纵坐标为.
将点代入直线中得,
直线的解析式为;
(2)如图2,连接,由(1)知,.
的面积是的面积的2倍,,由(1)知,直线的解析式为.令,则.
设点的纵坐标为.
由(1)知,双曲线的解析式为.
点在双曲线上,,2);
(4)由(1)知,,由图象知,不等式的解集为:或.
339.【解】(1)对于.令,解得.令,则,故点、的坐标分别为为直角,则是圆的直径,由点、的坐标得:,故圆的半径;
(2)过点作于点.设直线与圆切于点,连接,则,
则,
在Rt中,,即直线向上平移个单位得到,
故的表达式为;
(3)由直线的表达式知,点,联立的表达式和反比例函数表达式并整理得:,解得:或,故点的坐标为,由点、的坐标,坐标公式得:,则的面积.
340.【解】(1)过点,即反比例函数:.
当时,,即.
过和,则,解得:.
(2)当时,代入中得,,即.
且或;
(3)如图,设与的图象交于两点,向下平移两个单位得,且,
,联立得:,解得:或
或.
341.【解】(1)对于①,当时,,故点,即,则,故点的坐标为,点的坐标为;
(2)由(1)知,点.设直线的表达式为,则,解得:,故直线的表达式为.设直线交轴于点,则点.
同理可得,直线的表达式为,联立、的表达式并解得:,故点的纵坐标为,则点到轴的距离为;
(3)存在,理由:由直线的表达式知,点,由点的坐标知,,则,由点、的坐标知,.
①当点在上方时(∥,如图,过点作直线∥交轴于点,过点作于点,则的面积,解得
∥,则,在Rt中,,解得,则,故点,则直线的表达式为 ②,联立①②并解得:或,故点的坐标为或;
②当点在下方时(∥),同理可得,点的坐标为.
综上所述,点的坐标为或或.
21世纪教育网(www.21cnjy.com)
同课章节目录
