【中考数学几何模型】第十七节:反比例函数342-350(含答案)
文档属性
| 名称 | 【中考数学几何模型】第十七节:反比例函数342-350(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 17:13:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第十七节:反比例函数
342.反比例函数图像菱形存在性问题(初三)
如图,矩形的顶点分别落在轴,轴的正半轴上,顶点,反比例函数的图象与分别交于.
(1)求反比例函数关系式和点的坐标;
(2)写出与的位置关系并说明理由;
(3)点在直线上,点是平面内一点,当四边形为菱形时,求出点的坐标并判断点是否在反比例函数图象上.
343.反比例函数图像等腰三角形存在性问题(初三)
如图,一次函数的图象与两坐标轴分别交于两点,与反比例函数的图象交于点.
(1)求反比例函数的解析式;
(2)若点在轴正半轴上,且与点构成以为腰的等腰三角形,请直接写出所有符合条件的点坐标.
344.反比例函数与正比例函数直角存在性问题(初三)
如图,正比例函数的图象与反比例函数的图象交于点和点.
(1)________,________;
(2)点在y轴正半轴上.,求点的坐标;
(3)点在轴上,为锐角,直接写出的取值范围.
345.反比例函数代数几何综合题(初三)
如图所示,的顶点在反比例函数的图象上,直线交轴于点,且点的纵坐标为5,过点分别作轴的垂线,垂足分别为点,且.
(1)若点为线段的中点,求的值;
(2)若为等腰直角三角形,,其面积小于3.
①求证:;
②把称为两点间的“距离”,记为,求的值.
346.反比例函数矩形平行四边形综合题(初三)
如图,点是反比例函数图象上一点,过点分别向坐标轴作垂线,垂足为.反比例函数的图象经过的中点,与,分别相交于点.连接并延长交轴于点,点与点关于点对称,连接.
(1)填空:________;
(2)求的面积;
(3)求证:四边形BDFG为平行四边形.
347.反比例函数图像将军饮马周长最小值(初三)
如图,在矩形中,,点是边的中点,反比例函数的图象经过点,交边于点,直线的解析式为.
(1)求反比例函数的解析式和直线的解析式;
(2)在y轴上找一点,使的周长最小,求出此时点的坐标;
(3)在(2)的条件下,的周长最小值是________.
348.反比例函数图像与圆的综合题(初三)
如图,在平面直角坐标系中,与轴的正半轴交于两点,与轴的正半轴相切于点,连接,已知半径为,双曲线经过圆心.
(1)求双曲线的解析式;
(2)求直线的解析式.
349.反比例函数图像面积最大值问题(初三)
如图,平面直角坐标系中,为原点,点分别在轴、轴的正半轴上.的两条外角平分线交于点在反比例函数的图象上.的延长线交轴于点的延长线交轴于点,连接.
(1)求的度数及点的坐标;
(2)求的面积;
(3)的面积是否存在最大值 若存在,求出最大面积;若不存在,请说明理由.
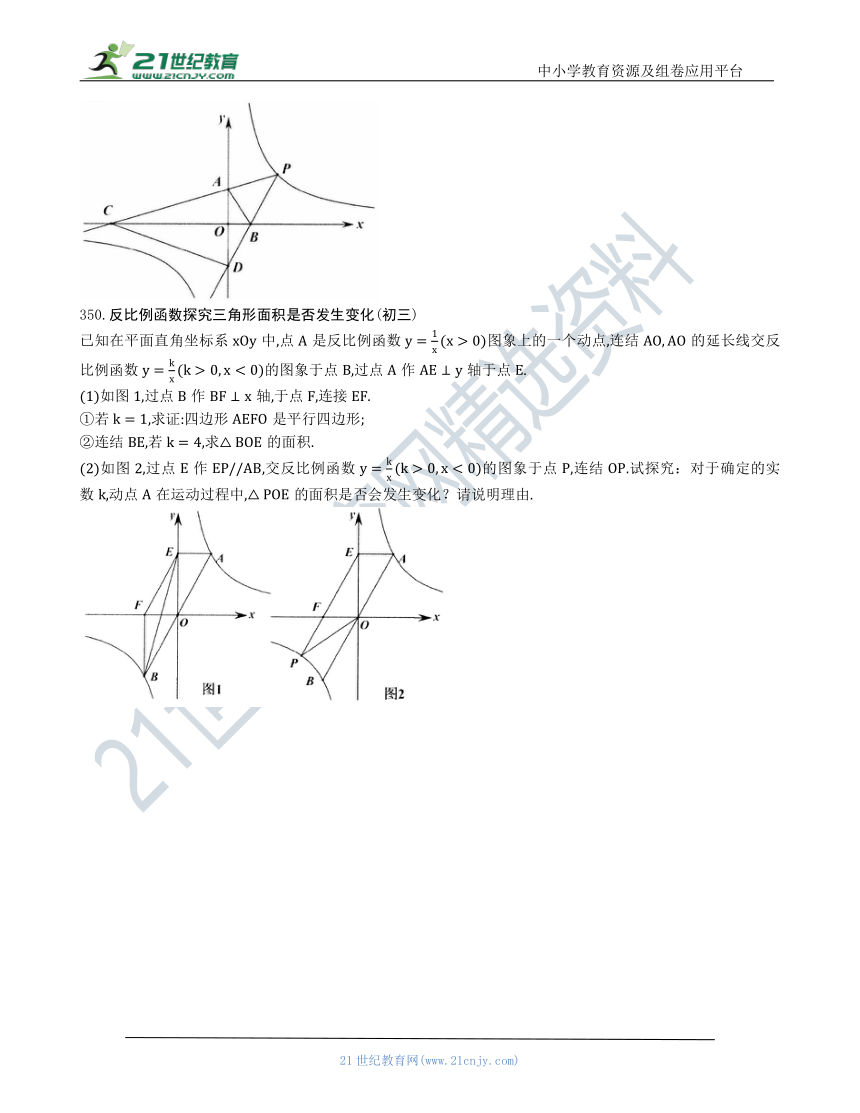
350.反比例函数探究三角形面积是否发生变化(初三)
已知在平面直角坐标系中,点是反比例函数图象上的一个动点,连结的延长线交反比例函数的图象于点,过点作轴于点.
(1)如图1,过点作轴,于点,连接.
①若,求证:四边形是平行四边形;
②连结,若,求的面积.
(2)如图2,过点作,交反比例函数的图象于点,连结.试探究:对于确定的实数,动点在运动过程中,的面积是否会发生变化?请说明理由.
答案
342.【解】(1),则,而,故点,将点的坐标代入反比例函数表达式得:,解得,故反比例函数表达式为,当时,,故点;
(2)由(1)知,,点,点,则,故∥;
(3)①当点在点的下方时,当点在点的右方时,如图,过点作轴于点.
四边形为菱形,则.在Rt中,,则,故,则,故点,则点,当时,,故点在反比例函数图象上;
②当点在点的上方时,同理可得,点,同理可得,点在反比例函数图象上;
综上,点的坐标为或都在反比例函数图象上.
343.【解】(1)点在一次函数的图象上,把点坐标代入,得点的坐标是,
设反比例函数的解析式为,把点的坐标(-2,3)代入得,,解得反比例函数的解析式为;
(2)在直线中,令,则,1),由(1)知,由点的距离公式得:,当时,.
当时,点在的垂直平分线,,即满足条件的点的坐标为或.
344.【解】(1)把代入反比例函数中,得,把代入正比例函数中,得,
故答案为:;
(2)由(1)可知,根据双曲线与正比例函数图象的对称性得,由点的距离公式可得:
;
(3)如图,在轴上原点的两旁取两点,使得.
四边形为矩形,.
点在轴上,为锐角,点必在的左边或的右边,或.
解法二:在轴上原点的两旁取两点,使得,则.
点在轴上,为锐角,点必在的左边或的右边,或.
345.【解】(1)点为线段的中点,,即:点坐标为.
又轴,.
(2)①在为等腰直角三角形中,.
又轴,.
在和中,,
②【解】设点坐标为.
设直线解析式为:,将两点代入得:则.解得.
当时,,符合;
当时,,不符舍去;综上所述:.
346.【解】(1)设点,则点,则,故答案为2;
(2)连接,则的面积的面积=
(3)设点,则点点与点关于点对称,故点,则点.
设直线的表达式为:,将点、的坐标代入上式得:并解得.
直线的表达式为:,
令,则,故点,
故,而,
又∥,故四边形为平行四边形.
347.【解】(1)点是边的中点,.
四边形是矩形,.
反比例函数的图象经过点反比例函数的解析式为.
当时,.把和,2)代入得,直线的解析式为;
(2)作点关于轴的对称点,连接交轴于,连接,此时,的周长最小,点的坐标为点的坐标为.
设直线的解析式为,
解得:直线的解析式为.
令,得点的坐标为;
(3).由(2)知,的坐标为的周长最小值,
故答案为:.
348.【解】(1)如图,过点作轴于.
切轴于.
四边形是矩形,.
.
在Rt中,
双曲线经过圆心双曲线的解析式为;
(2)由(1)知,四边形是矩形,.
在Rt中,.
.
设直线的解析式为,
,直线的解析式为.
349.【解】(1)如图,作于于于.
.
同理可证:.
四边形PMON是矩形,.
可以假设在上,.
.
(2)连接四边形是正方形.
(3)设,则
的面积的最大值为.
350.(1)①证明:设点的坐标为,则当点时,点的坐标为
轴,∥四边形是平行四边形;
②【解】过点作轴于点,如图1,轴,∥当时,,即;
(2)不改变.理由如下:
过点作轴丁点与轴交丁点.设点的坐标为,点的坐标为,则.
∥∥四边形是平行四边形,.
.
又
,解得
对于确定的实数,动点在运动过程中,的面积不会发生变化.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第十七节:反比例函数
342.反比例函数图像菱形存在性问题(初三)
如图,矩形的顶点分别落在轴,轴的正半轴上,顶点,反比例函数的图象与分别交于.
(1)求反比例函数关系式和点的坐标;
(2)写出与的位置关系并说明理由;
(3)点在直线上,点是平面内一点,当四边形为菱形时,求出点的坐标并判断点是否在反比例函数图象上.
343.反比例函数图像等腰三角形存在性问题(初三)
如图,一次函数的图象与两坐标轴分别交于两点,与反比例函数的图象交于点.
(1)求反比例函数的解析式;
(2)若点在轴正半轴上,且与点构成以为腰的等腰三角形,请直接写出所有符合条件的点坐标.
344.反比例函数与正比例函数直角存在性问题(初三)
如图,正比例函数的图象与反比例函数的图象交于点和点.
(1)________,________;
(2)点在y轴正半轴上.,求点的坐标;
(3)点在轴上,为锐角,直接写出的取值范围.
345.反比例函数代数几何综合题(初三)
如图所示,的顶点在反比例函数的图象上,直线交轴于点,且点的纵坐标为5,过点分别作轴的垂线,垂足分别为点,且.
(1)若点为线段的中点,求的值;
(2)若为等腰直角三角形,,其面积小于3.
①求证:;
②把称为两点间的“距离”,记为,求的值.
346.反比例函数矩形平行四边形综合题(初三)
如图,点是反比例函数图象上一点,过点分别向坐标轴作垂线,垂足为.反比例函数的图象经过的中点,与,分别相交于点.连接并延长交轴于点,点与点关于点对称,连接.
(1)填空:________;
(2)求的面积;
(3)求证:四边形BDFG为平行四边形.
347.反比例函数图像将军饮马周长最小值(初三)
如图,在矩形中,,点是边的中点,反比例函数的图象经过点,交边于点,直线的解析式为.
(1)求反比例函数的解析式和直线的解析式;
(2)在y轴上找一点,使的周长最小,求出此时点的坐标;
(3)在(2)的条件下,的周长最小值是________.
348.反比例函数图像与圆的综合题(初三)
如图,在平面直角坐标系中,与轴的正半轴交于两点,与轴的正半轴相切于点,连接,已知半径为,双曲线经过圆心.
(1)求双曲线的解析式;
(2)求直线的解析式.
349.反比例函数图像面积最大值问题(初三)
如图,平面直角坐标系中,为原点,点分别在轴、轴的正半轴上.的两条外角平分线交于点在反比例函数的图象上.的延长线交轴于点的延长线交轴于点,连接.
(1)求的度数及点的坐标;
(2)求的面积;
(3)的面积是否存在最大值 若存在,求出最大面积;若不存在,请说明理由.
350.反比例函数探究三角形面积是否发生变化(初三)
已知在平面直角坐标系中,点是反比例函数图象上的一个动点,连结的延长线交反比例函数的图象于点,过点作轴于点.
(1)如图1,过点作轴,于点,连接.
①若,求证:四边形是平行四边形;
②连结,若,求的面积.
(2)如图2,过点作,交反比例函数的图象于点,连结.试探究:对于确定的实数,动点在运动过程中,的面积是否会发生变化?请说明理由.
答案
342.【解】(1),则,而,故点,将点的坐标代入反比例函数表达式得:,解得,故反比例函数表达式为,当时,,故点;
(2)由(1)知,,点,点,则,故∥;
(3)①当点在点的下方时,当点在点的右方时,如图,过点作轴于点.
四边形为菱形,则.在Rt中,,则,故,则,故点,则点,当时,,故点在反比例函数图象上;
②当点在点的上方时,同理可得,点,同理可得,点在反比例函数图象上;
综上,点的坐标为或都在反比例函数图象上.
343.【解】(1)点在一次函数的图象上,把点坐标代入,得点的坐标是,
设反比例函数的解析式为,把点的坐标(-2,3)代入得,,解得反比例函数的解析式为;
(2)在直线中,令,则,1),由(1)知,由点的距离公式得:,当时,.
当时,点在的垂直平分线,,即满足条件的点的坐标为或.
344.【解】(1)把代入反比例函数中,得,把代入正比例函数中,得,
故答案为:;
(2)由(1)可知,根据双曲线与正比例函数图象的对称性得,由点的距离公式可得:
;
(3)如图,在轴上原点的两旁取两点,使得.
四边形为矩形,.
点在轴上,为锐角,点必在的左边或的右边,或.
解法二:在轴上原点的两旁取两点,使得,则.
点在轴上,为锐角,点必在的左边或的右边,或.
345.【解】(1)点为线段的中点,,即:点坐标为.
又轴,.
(2)①在为等腰直角三角形中,.
又轴,.
在和中,,
②【解】设点坐标为.
设直线解析式为:,将两点代入得:则.解得.
当时,,符合;
当时,,不符舍去;综上所述:.
346.【解】(1)设点,则点,则,故答案为2;
(2)连接,则的面积的面积=
(3)设点,则点点与点关于点对称,故点,则点.
设直线的表达式为:,将点、的坐标代入上式得:并解得.
直线的表达式为:,
令,则,故点,
故,而,
又∥,故四边形为平行四边形.
347.【解】(1)点是边的中点,.
四边形是矩形,.
反比例函数的图象经过点反比例函数的解析式为.
当时,.把和,2)代入得,直线的解析式为;
(2)作点关于轴的对称点,连接交轴于,连接,此时,的周长最小,点的坐标为点的坐标为.
设直线的解析式为,
解得:直线的解析式为.
令,得点的坐标为;
(3).由(2)知,的坐标为的周长最小值,
故答案为:.
348.【解】(1)如图,过点作轴于.
切轴于.
四边形是矩形,.
.
在Rt中,
双曲线经过圆心双曲线的解析式为;
(2)由(1)知,四边形是矩形,.
在Rt中,.
.
设直线的解析式为,
,直线的解析式为.
349.【解】(1)如图,作于于于.
.
同理可证:.
四边形PMON是矩形,.
可以假设在上,.
.
(2)连接四边形是正方形.
(3)设,则
的面积的最大值为.
350.(1)①证明:设点的坐标为,则当点时,点的坐标为
轴,∥四边形是平行四边形;
②【解】过点作轴于点,如图1,轴,∥当时,,即;
(2)不改变.理由如下:
过点作轴丁点与轴交丁点.设点的坐标为,点的坐标为,则.
∥∥四边形是平行四边形,.
.
又
,解得
对于确定的实数,动点在运动过程中,的面积不会发生变化.
21世纪教育网(www.21cnjy.com)
同课章节目录
