【中考数学几何模型】第二十八节:圆的计算证明辅助线压轴题479--485(含答案)
文档属性
| 名称 | 【中考数学几何模型】第二十八节:圆的计算证明辅助线压轴题479--485(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 404.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第二十八节:圆的计算证明辅助线压轴题
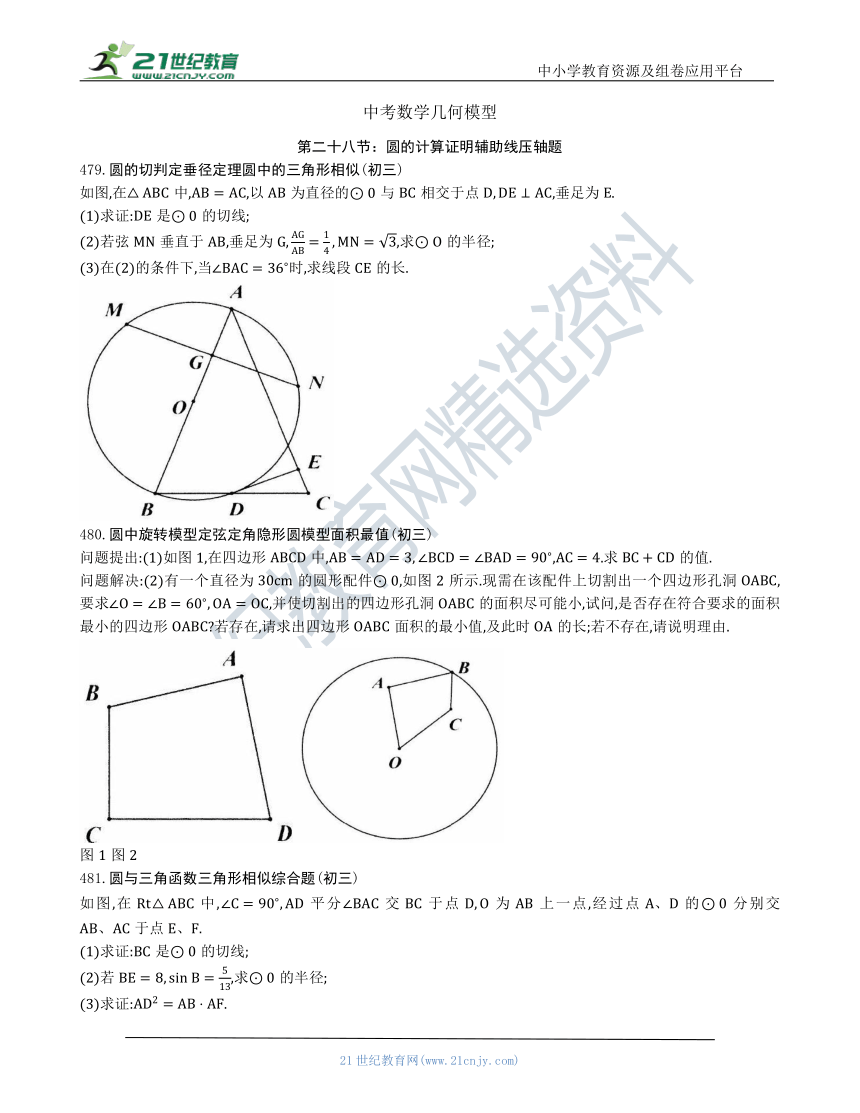
479.圆的切判定垂径定理圆中的三角形相似(初三)
如图,在中,,以为直径的与相交于点,垂足为.
(1)求证:是的切线;
(2)若弦垂直于,垂足为,求的半径;
(3)在(2)的条件下,当时,求线段的长.
480.圆中旋转模型定弦定角隐形圆模型面积最值(初三)
问题提出:(1)如图1,在四边形中,,.求的值.
问题解决:(2)有一个直径为的圆形配件,如图2所示.现需在该配件上切割出一个四边形孔洞,要求,并使切割出的四边形孔洞的面积尽可能小,试问,是否存在符合要求的面积最小的四边形 若存在,请求出四边形面积的最小值,及此时的长;若不存在,请说明理由.
图1图2
481.圆与三角函数三角形相似综合题(初三)
如图,在Rt中,平分交于点为上一点,经过点的分别交于点.
(1)求证:是的切线;
(2)若,求的半径;
(3)求证:.
482.圆中三角形相似和动点有关的定值(初三)
如图,在中,为直径,为上一点,为常数,且.过点的弦为上一动点(与点不重合),,垂足为.连接.
(1)若.(1)求证:;(2)求的值;
(2)用含的代数式表示,请直接写出结果;
(3)存在一个大小确定的,对于点的任意位置,都有的值是一个定值,求此时的度数.
483.圆和三角形相似综合题(初三)
如图,是的外接圆,点在边上,的平分线交于点,连接,过点作的切线与的延长线交于点.
(1)求证:;
(2)求证:;
(3)当时,求线段的长.
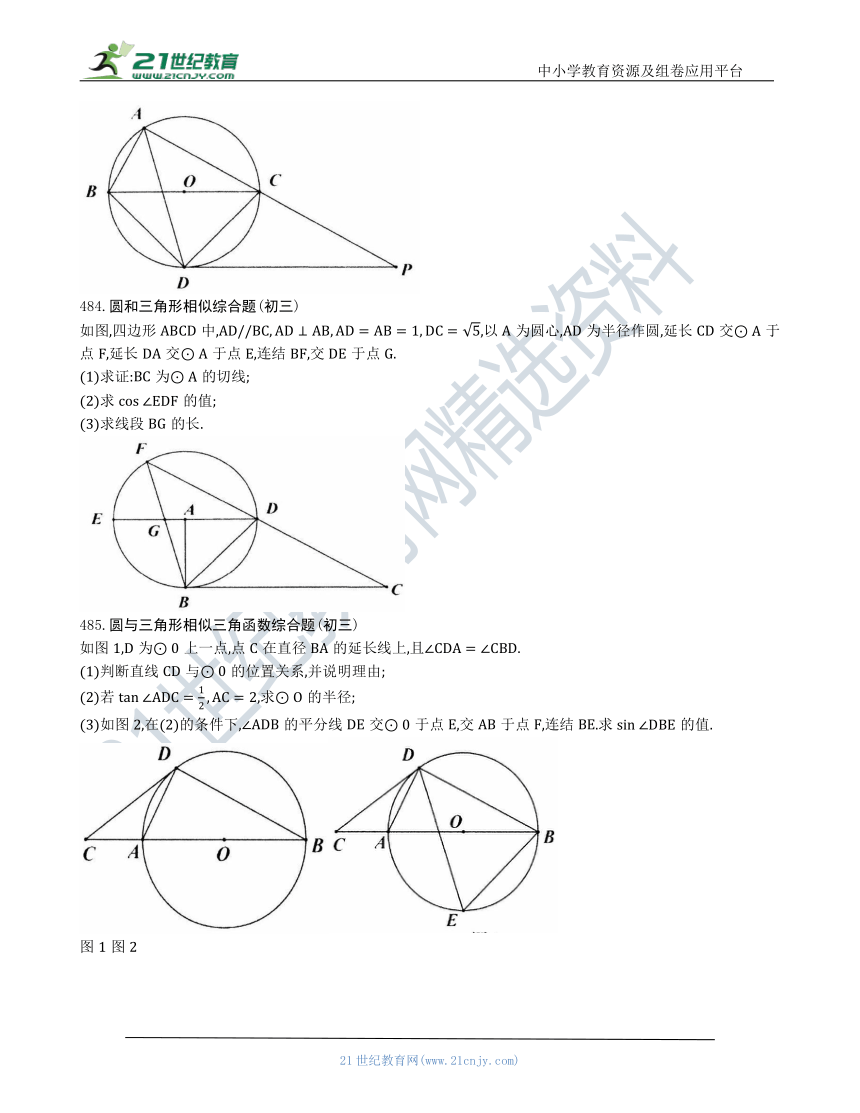
484.圆和三角形相似综合题(初三)
如图,四边形中,,以为圆心,为半径作圆,延长交于点,延长交于点,连结,交于点.
(1)求证:为的切线;
(2)求的值;
(3)求线段的长.
485.圆与三角形相似三角函数综合题(初三)
如图1,为上一点,点在直径的延长线上,且.
(1)判断直线与的位置关系,并说明理由;
(2)若,求的半径;
(3)如图2,在(2)的条件下,的平分线交于点,交于点,连结.求的值.
图1图2
答案
479.(1)证明:如图1,连接
是的半径是的切线;
(2)【解】如图1,连接且为
的直径
设的半径为则
在Rt中,根据勾股定理得
即的半径为1;
图1图2
(3)如图2,作的平分线交于
在中
设在中
由(2)知的半径为
或(舍),
连接为的直径,
.
此时.
480.【解】(1)如图1
可以将绕点逆时针旋转得
在同一条直线上,
;
图1
(2)如图2,连接
将绕点顺时针旋转至连接
是等边三角形,
当的面积最大时,四边形的面积最小
均为定值
是外接圆的弧上运动,作它的外接圆当时即为底边上的高的最大值,此时O、C、F、I四点共线.
图1图2
(3)如图2,连接是直径,
又
又
.
481.【解】(1)如图1,连接,则,是的平分线,
,
,
点在上,是的切线;
(2),
的半径为5;
(3)如图2,连接是直径
482.【解】(1)(1)连接如图1:
即
是中点,又是的垂直平分线,
即是等边三角形,
;
(2)连接如图1:是直径
由(1)知:;
(2)连接如图2:
是直径
又
与(1)中(2)同理,可得:
;
在等腰Rt中
图1图2图3
(3)由(2)得
即
若是定值,则的值与无关,
即当时的定值为1,此时与重合,
如图3
是等腰直角三角形
故存在半径为1的对的任意位置,都有是定值1,此时为.
483.【解】(1)连接是的切线是的平分线
是圆的直径
;
(2)
;
(3)
在等腰Rt中
.
484.(1)证明:
又是圆的半径为的切线;
(2)【解】如图1,过点作于
由(1)知
四边形为矩形
矩形是正方形
在Rt中根据勾股定理得,
;
(3)如图2,过点作于
则
在Rt中
由(2)知
在Rt中.
485.【解】(1)与相切,
理由:如图1,连接
为的直径
与相切;
(2)由(1)知
在Rt中
的半径为3;
图1图2
(3)如图2,连接过点作于
平分
在Rt中
设则
在Rt中
或(舍)
.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第二十八节:圆的计算证明辅助线压轴题
479.圆的切判定垂径定理圆中的三角形相似(初三)
如图,在中,,以为直径的与相交于点,垂足为.
(1)求证:是的切线;
(2)若弦垂直于,垂足为,求的半径;
(3)在(2)的条件下,当时,求线段的长.
480.圆中旋转模型定弦定角隐形圆模型面积最值(初三)
问题提出:(1)如图1,在四边形中,,.求的值.
问题解决:(2)有一个直径为的圆形配件,如图2所示.现需在该配件上切割出一个四边形孔洞,要求,并使切割出的四边形孔洞的面积尽可能小,试问,是否存在符合要求的面积最小的四边形 若存在,请求出四边形面积的最小值,及此时的长;若不存在,请说明理由.
图1图2
481.圆与三角函数三角形相似综合题(初三)
如图,在Rt中,平分交于点为上一点,经过点的分别交于点.
(1)求证:是的切线;
(2)若,求的半径;
(3)求证:.
482.圆中三角形相似和动点有关的定值(初三)
如图,在中,为直径,为上一点,为常数,且.过点的弦为上一动点(与点不重合),,垂足为.连接.
(1)若.(1)求证:;(2)求的值;
(2)用含的代数式表示,请直接写出结果;
(3)存在一个大小确定的,对于点的任意位置,都有的值是一个定值,求此时的度数.
483.圆和三角形相似综合题(初三)
如图,是的外接圆,点在边上,的平分线交于点,连接,过点作的切线与的延长线交于点.
(1)求证:;
(2)求证:;
(3)当时,求线段的长.
484.圆和三角形相似综合题(初三)
如图,四边形中,,以为圆心,为半径作圆,延长交于点,延长交于点,连结,交于点.
(1)求证:为的切线;
(2)求的值;
(3)求线段的长.
485.圆与三角形相似三角函数综合题(初三)
如图1,为上一点,点在直径的延长线上,且.
(1)判断直线与的位置关系,并说明理由;
(2)若,求的半径;
(3)如图2,在(2)的条件下,的平分线交于点,交于点,连结.求的值.
图1图2
答案
479.(1)证明:如图1,连接
是的半径是的切线;
(2)【解】如图1,连接且为
的直径
设的半径为则
在Rt中,根据勾股定理得
即的半径为1;
图1图2
(3)如图2,作的平分线交于
在中
设在中
由(2)知的半径为
或(舍),
连接为的直径,
.
此时.
480.【解】(1)如图1
可以将绕点逆时针旋转得
在同一条直线上,
;
图1
(2)如图2,连接
将绕点顺时针旋转至连接
是等边三角形,
当的面积最大时,四边形的面积最小
均为定值
是外接圆的弧上运动,作它的外接圆当时即为底边上的高的最大值,此时O、C、F、I四点共线.
图1图2
(3)如图2,连接是直径,
又
又
.
481.【解】(1)如图1,连接,则,是的平分线,
,
,
点在上,是的切线;
(2),
的半径为5;
(3)如图2,连接是直径
482.【解】(1)(1)连接如图1:
即
是中点,又是的垂直平分线,
即是等边三角形,
;
(2)连接如图1:是直径
由(1)知:;
(2)连接如图2:
是直径
又
与(1)中(2)同理,可得:
;
在等腰Rt中
图1图2图3
(3)由(2)得
即
若是定值,则的值与无关,
即当时的定值为1,此时与重合,
如图3
是等腰直角三角形
故存在半径为1的对的任意位置,都有是定值1,此时为.
483.【解】(1)连接是的切线是的平分线
是圆的直径
;
(2)
;
(3)
在等腰Rt中
.
484.(1)证明:
又是圆的半径为的切线;
(2)【解】如图1,过点作于
由(1)知
四边形为矩形
矩形是正方形
在Rt中根据勾股定理得,
;
(3)如图2,过点作于
则
在Rt中
由(2)知
在Rt中.
485.【解】(1)与相切,
理由:如图1,连接
为的直径
与相切;
(2)由(1)知
在Rt中
的半径为3;
图1图2
(3)如图2,连接过点作于
平分
在Rt中
设则
在Rt中
或(舍)
.
21世纪教育网(www.21cnjy.com)
同课章节目录
