【中考数学几何模型】第二十九节:图形变换多解选填压轴题492-500(含答案)
文档属性
| 名称 | 【中考数学几何模型】第二十九节:图形变换多解选填压轴题492-500(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 17:06:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第二十九节:图形变换多解选填压轴题
492.特殊直角三角形动点多解分类讨论(初二)
在Rt中,,有一个锐角为.若点在直线上(不与点重合),且,则的长为________.
493.矩形折叠直角三角形存在性多解分类讨论(初二)
在矩形纸片中,是边上的点,将纸片沿折叠,使点落在点处,连接,当为直角三角形时,的长为________.
494.菱形翻折对应点落在对角线上多解题(初三)
如图,在菱形中,,点为边上一点,,点为边上的一动点,沿将翻折,点落在点处,当点在菱形的对角线上时,的长度为________.
495.矩形折叠对应点落在对角线上多解分类讨论(初三)
如图,在矩形中,,点为的中点,点为边上的一动点,将
沿折叠,点落在点处,当点在矩形的对角线上时,的长度为________.
496.矩形边上的动点等腰三角形存在性问题多解(初二)
如图,在矩形中,,若点在边上,连接是以为腰的等腰三角形,则的长为_______.
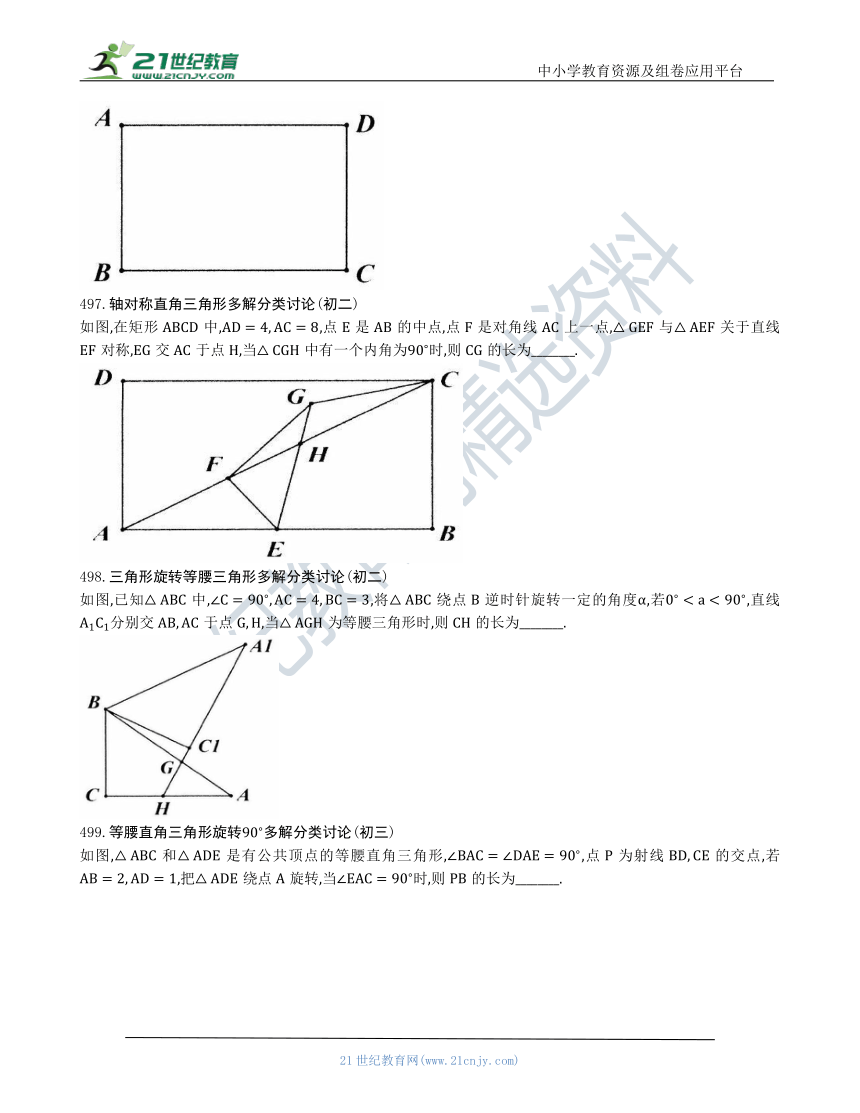
497.轴对称直角三角形多解分类讨论(初二)
如图,在矩形中,,点是的中点,点是对角线上一点,与关于直线对称,交于点,当中有一个内角为时,则的长为________.
498.三角形旋转等腰三角形多解分类讨论(初二)
如图,已知中,,将绕点逆时针旋转一定的角度,若,直线分别交于点,当为等腰三角形时,则的长为________.
499.等腰直角三角形旋转多解分类讨论(初三)
如图,和是有公共顶点的等腰直角三角形,,点为射线的交点,若,把绕点旋转,当时,则的长为________.
500.直角三角形双动点多解分类讨论(初二)
如图,中,是上的动点,是上的动点(不与重合).
(1)线段PA的最小值为________.
(2)当为直角三角形时,也为直角三角形时,则的长度为________.
答案
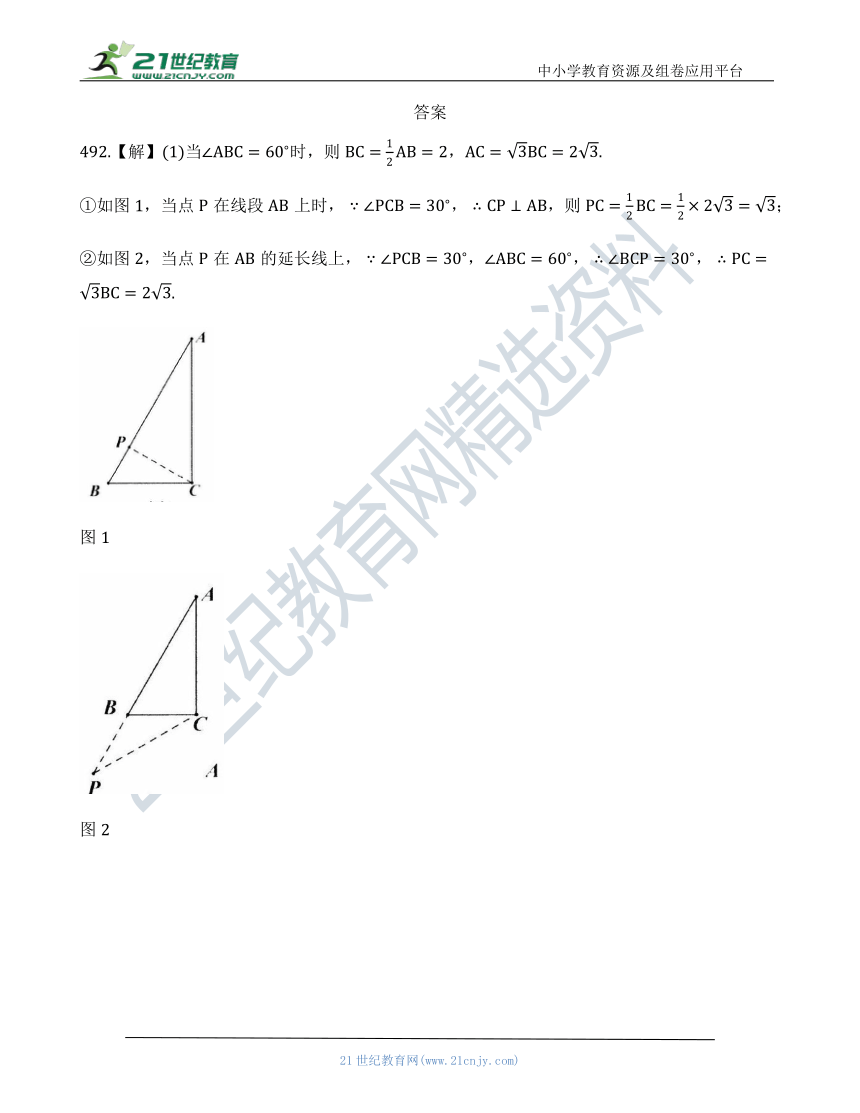
492.【解】(1)当时,则.
①如图1,当点在线段上时则;
②如图2,当点在的延长线上.
图1
图2
图3
(2)当时,如图3
为等边三角形.
.
.综上的长为:2或或.故答案为2或或.
493.【解】四边形为矩形,
.
为直角二角形分两种情况:
(1)当时,如图1所示.
点在对角线上平分
;
图1
图2
(2)当时,如图2所示.
四边形为正方形.
综上所述:的长为3或6.故答案为:3或6.
494.【解】分两种情况:
(1).如图1,当点在菱形对角线上时,:由折叠的性质得:四边形是菱形
2;
(2).如图2,当点在菱形对角线上时,设
由折叠的性质得:
四边形是菱形
即
解得:或(不合题意舍去)
综上所述的长为2或;
故答案为:2或.
495.【解】分两种情况讨论:
第一种情况:如图1,当点落在上时,
点为的中点
将沿折叠,点落在点处,
;
图1图2
第二种情况,如图2,若点落在上时,连接交于点将沿折叠
又
故答案为:或.
496.【解】如图,在矩形中.为腰的等腰三角形,有两种情况:
第一种情况:如图1,当时,点是的中垂线与的交点,则.
在Rt中,由勾股定理得;第二种情况:如图2,当时也是以为腰的等腰三角形.
综上所述的长度是5或6.
故答案为:5或6.
图1
图2
497.【解】四边形是矩形,
点是的中点
当中有一个内角为时,根据题意不会等于现在分两种情况讨论:
(1)当时,如图1,连接
则在Rt和Rt中
RtRt;
(2)如图2,当时,则
由折叠的性质得:
;
综上所述,当中有一个内角为时,则的长为4或;
故答案为:4或.
图1
图2
498.【解】如图1中,当时
.
图1
图2
如图2中,当时,过点作于.同法可证设
则有解得
.
综上所述,满足条件的的值为或1.
499.【解】和是等腰直角三角形
(1)当点在上时
;
(2)当点在延长线上时
综上所述的长为或.
故答案为:或.
500.【解】(1)如图1,由垂线段最短可知,作
于此时就是最小值
中
线段的最小值为.故答案为:3;
|图1
(2)当为直角三角形时也为直角三角形,一共有3种不同的情况:
第一种情况:如图2时;
图2
第二种情况:如图3时即
解得(负值舍去),
过点作于点
图3
图4
第三种情况,如图4时,同第二种情况,可得
.
综上所述的长度为4.5或4或3.
故答案为:4.5或4或3.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第二十九节:图形变换多解选填压轴题
492.特殊直角三角形动点多解分类讨论(初二)
在Rt中,,有一个锐角为.若点在直线上(不与点重合),且,则的长为________.
493.矩形折叠直角三角形存在性多解分类讨论(初二)
在矩形纸片中,是边上的点,将纸片沿折叠,使点落在点处,连接,当为直角三角形时,的长为________.
494.菱形翻折对应点落在对角线上多解题(初三)
如图,在菱形中,,点为边上一点,,点为边上的一动点,沿将翻折,点落在点处,当点在菱形的对角线上时,的长度为________.
495.矩形折叠对应点落在对角线上多解分类讨论(初三)
如图,在矩形中,,点为的中点,点为边上的一动点,将
沿折叠,点落在点处,当点在矩形的对角线上时,的长度为________.
496.矩形边上的动点等腰三角形存在性问题多解(初二)
如图,在矩形中,,若点在边上,连接是以为腰的等腰三角形,则的长为_______.
497.轴对称直角三角形多解分类讨论(初二)
如图,在矩形中,,点是的中点,点是对角线上一点,与关于直线对称,交于点,当中有一个内角为时,则的长为________.
498.三角形旋转等腰三角形多解分类讨论(初二)
如图,已知中,,将绕点逆时针旋转一定的角度,若,直线分别交于点,当为等腰三角形时,则的长为________.
499.等腰直角三角形旋转多解分类讨论(初三)
如图,和是有公共顶点的等腰直角三角形,,点为射线的交点,若,把绕点旋转,当时,则的长为________.
500.直角三角形双动点多解分类讨论(初二)
如图,中,是上的动点,是上的动点(不与重合).
(1)线段PA的最小值为________.
(2)当为直角三角形时,也为直角三角形时,则的长度为________.
答案
492.【解】(1)当时,则.
①如图1,当点在线段上时则;
②如图2,当点在的延长线上.
图1
图2
图3
(2)当时,如图3
为等边三角形.
.
.综上的长为:2或或.故答案为2或或.
493.【解】四边形为矩形,
.
为直角二角形分两种情况:
(1)当时,如图1所示.
点在对角线上平分
;
图1
图2
(2)当时,如图2所示.
四边形为正方形.
综上所述:的长为3或6.故答案为:3或6.
494.【解】分两种情况:
(1).如图1,当点在菱形对角线上时,:由折叠的性质得:四边形是菱形
2;
(2).如图2,当点在菱形对角线上时,设
由折叠的性质得:
四边形是菱形
即
解得:或(不合题意舍去)
综上所述的长为2或;
故答案为:2或.
495.【解】分两种情况讨论:
第一种情况:如图1,当点落在上时,
点为的中点
将沿折叠,点落在点处,
;
图1图2
第二种情况,如图2,若点落在上时,连接交于点将沿折叠
又
故答案为:或.
496.【解】如图,在矩形中.为腰的等腰三角形,有两种情况:
第一种情况:如图1,当时,点是的中垂线与的交点,则.
在Rt中,由勾股定理得;第二种情况:如图2,当时也是以为腰的等腰三角形.
综上所述的长度是5或6.
故答案为:5或6.
图1
图2
497.【解】四边形是矩形,
点是的中点
当中有一个内角为时,根据题意不会等于现在分两种情况讨论:
(1)当时,如图1,连接
则在Rt和Rt中
RtRt;
(2)如图2,当时,则
由折叠的性质得:
;
综上所述,当中有一个内角为时,则的长为4或;
故答案为:4或.
图1
图2
498.【解】如图1中,当时
.
图1
图2
如图2中,当时,过点作于.同法可证设
则有解得
.
综上所述,满足条件的的值为或1.
499.【解】和是等腰直角三角形
(1)当点在上时
;
(2)当点在延长线上时
综上所述的长为或.
故答案为:或.
500.【解】(1)如图1,由垂线段最短可知,作
于此时就是最小值
中
线段的最小值为.故答案为:3;
|图1
(2)当为直角三角形时也为直角三角形,一共有3种不同的情况:
第一种情况:如图2时;
图2
第二种情况:如图3时即
解得(负值舍去),
过点作于点
图3
图4
第三种情况,如图4时,同第二种情况,可得
.
综上所述的长度为4.5或4或3.
故答案为:4.5或4或3.
21世纪教育网(www.21cnjy.com)
同课章节目录
