【中考数学几何模型】第二十六节:二次函数面积问题456-467(含答案)
文档属性
| 名称 | 【中考数学几何模型】第二十六节:二次函数面积问题456-467(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 611.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 17:07:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第二十六节:二次函数面积问题
456.二次函数三角形面积最大值铅垂定理(初三)
如图,已知抛物线经过两点,且其对称轴为直线.
(1)求此拋物线的解析式;
(2)若点是抛物线上点与点之间的动点(不包括点,点),求的面积的最大值,并求出此时点的坐标.
457.二次函数面积相等动点问题胡不归最小值问题(初三)
如图,在平面直角坐标系中,已知直线与轴交于点,与轴交于点,过两点的抛物线与轴交于另一点.
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点,使 若存在,请求出点的坐标,若不存在,请说明理由;
(3)点为直线下方抛物线上一点,点为轴上一点,当的面积最大时,求的最小值.
458.二次函数面积最大值问题胡不归最小值问题(初三)
在平面直角坐标系中,将二次函数)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与轴交于点(点在点的左侧),,经过点的一次函数的图象与轴正半轴交于点,且与抛物线的另一个交点为的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点在一次函数的图象下方,求面积的最大值,并求出此时点的坐标;
(3)若点为轴上任意一点,在(2)的结论下,求的最小值.
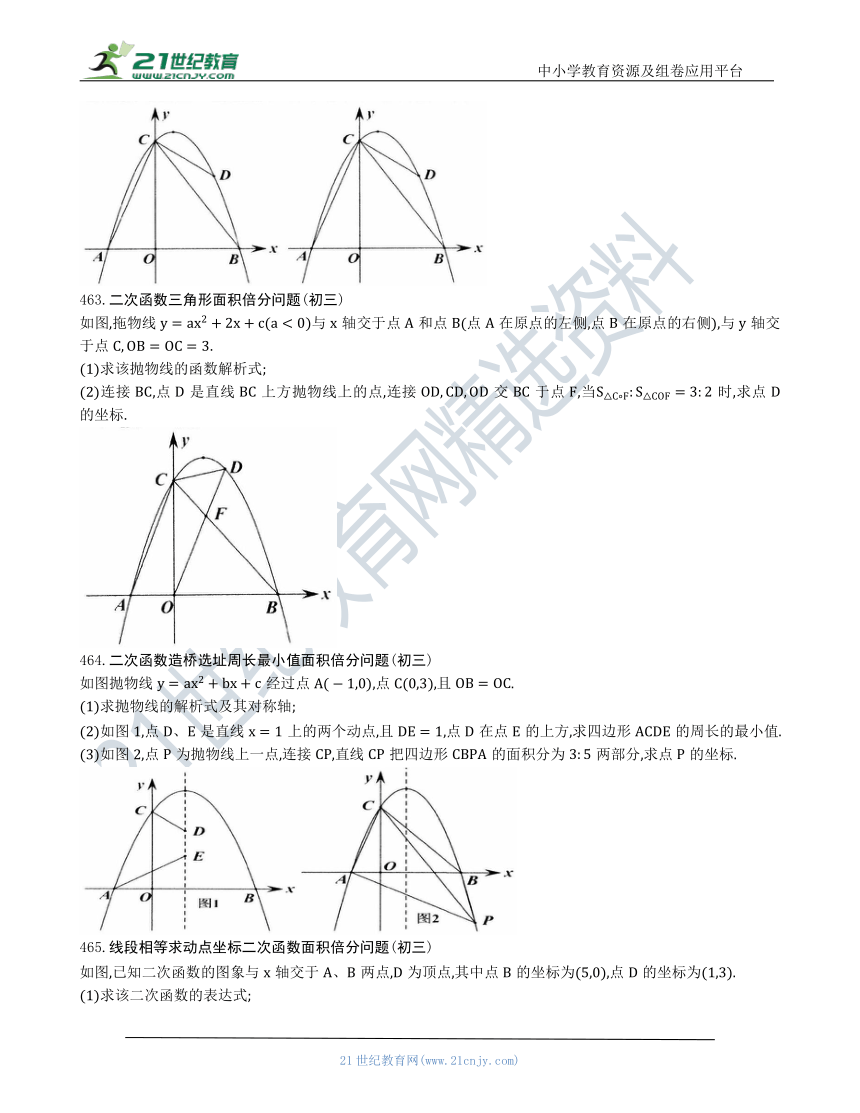
459.二次函数面积最大值周长最小值求点的坐标(初三)
已知抛物线经过点,与轴交于点.
(1)求这条抛物线的解析式;
(2)如图1,点是第三象限内抛物线上的一个动点,当四边形的面积最大时,求点的坐标;
(3)如图2,线段的垂直平分线交轴于点,垂足为D,为抛物线的顶点,在直线上是否存在一点,使的周长最小 若存在,求出点的坐标;若不存在,请说明理由.
460.二次函数三角形相似存在性问题三角形面积最大值(初三)
如图,在平面直角坐标系中,抛物线与轴交于点,点,与轴交于点,连接.又已知位于轴右侧且垂直于轴的动直线1,沿轴正方向从0运动到(不含0点和点),且分别交抛物线、线段以及轴于点.
(1)求抛物线的表达式;
(2)连接,当直线1运动时,求使得和相似的点的坐标;
(3)作,垂足为,当直线1运动时,求面积的最大值.
461.二次函数将军饮马周长最小值面积相等问题(初三)
如图,抛物线的图象过点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点,使得的周长最小,若存在,请求出点的坐标及的周长;若不存在,请说明理由;
(3)在(2)的条件下,在轴上方的抛物线上是否存在点(不与点重合),使得 若存在,请求出点的坐标;若不存在,请说明理由.
462.二次函数面积倍分问题平行四边形存在性问题(初三)
如图,抛物线经过两点,与轴交于点,点是抛物线上一动点,设点的横坐标为,连接DC.
(1)求抛物线的函数表达式.
(2)当的面积等于的面积的时,求的值.
(3)当时,若点是轴上一动点,点是抛物线上一动点,试判断是否存在这样的点,使得以点为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
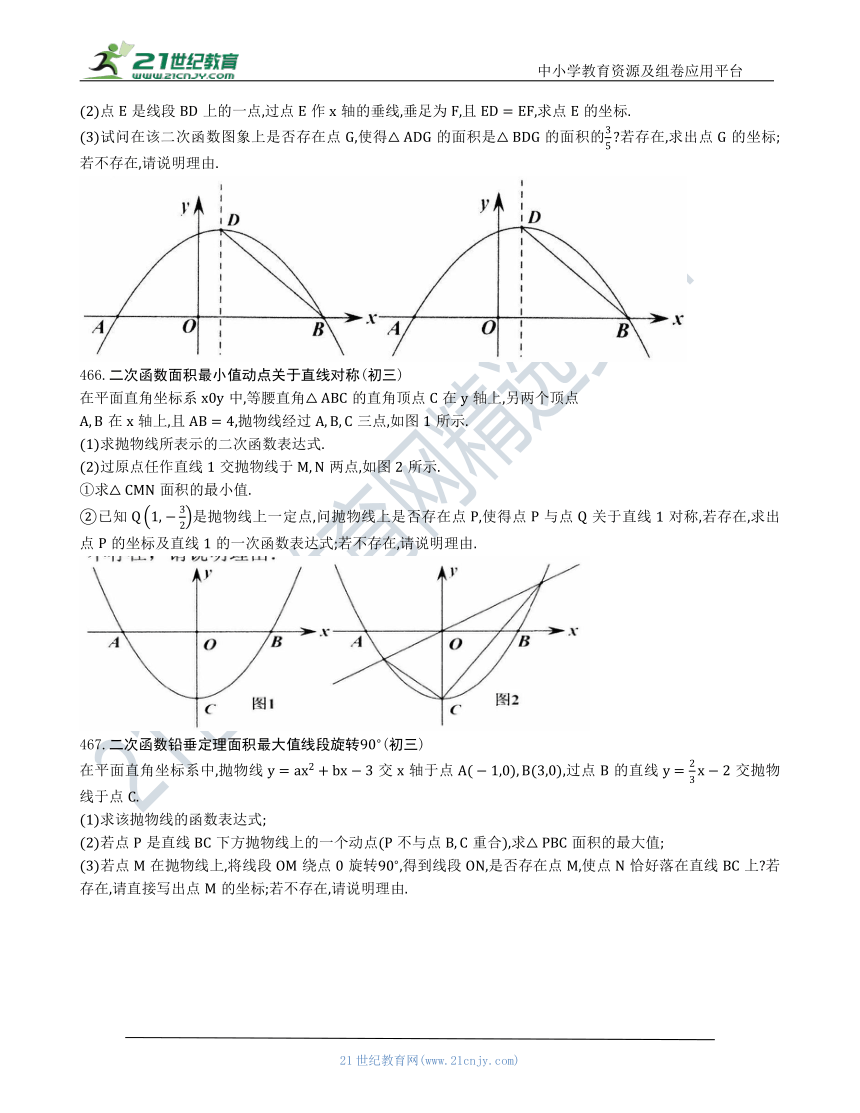
463.二次函数三角形面积倍分问题(初三)
如图,拖物线与轴交于点和点(点在原点的左侧,点在原点的右侧),与轴交于点.
(1)求该抛物线的函数解析式;
(2)连接,点是直线上方抛物线上的点,连接交于点,当时,求点的坐标.
464.二次函数造桥选址周长最小值面积倍分问题(初三)
如图抛物线经过点,点,且.
(1)求抛物线的解析式及其对称轴;
(2)如图1,点是直线上的两个动点,且,点在点的上方,求四边形ACDE的周长的最小值.
(3)如图2,点为抛物线上一点,连接,直线把四边形的面积分为两部分,求点的坐标.
465.线段相等求动点坐标二次函数面积倍分问题(初三)
如图,已知二次函数的图象与轴交于两点,为顶点,其中点的坐标为,点的坐标为.
(1)求该二次函数的表达式;
(2)点是线段上的一点,过点作轴的垂线,垂足为,且,求点的坐标.
(3)试问在该二次函数图象上是否存在点,使得的面积是的面积的若存在,求出点的坐标;若不存在,请说明理由.
466.二次函数面积最小值动点关于直线对称(初三)
在平面直角坐标系中,等腰直角的直角顶点在轴上,另两个顶点
在轴上,且,抛物线经过三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线1交抛物线于两点,如图2所示.
①求面积的最小值.
②已知是抛物线上一定点,问抛物线上是否存在点,使得点与点关于直线1对称,若存在,求出点的坐标及直线1的一次函数表达式;若不存在,请说明理由.
467.二次函数铅垂定理面积最大值线段旋转(初三)
在平面直角坐标系中,抛物线交轴于点,过点的直线交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点是直线下方抛物线上的一个动点(不与点重合),求面积的最大值;
(3)若点在抛物线上,将线段绕点0旋转,得到线段,是否存在点,使点恰好落在直线上 若存在,请直接写出点的坐标;若不存在,请说明理由.
答案
456.【解】(1)抛物线对称轴是直线且经过点,由抛物线的对称性可知:抛物线还经过点,,设抛物线的解析式为即:
把代入得:
抛物线的解析式为:.
(2)设直线的解析式为,直线为,
如图,作轴,交直线于,
设,则,
,此时,,
的面积的最大值为,
此时点的坐标为
457.【解】(1)直线与轴交于点,与轴交于点点,点,
点,点设抛物线解析式为:,
把点代入得:,
抛物线解析式为:;
(2)存在,分两种情况讨论:
①当点在直线上方时,过点作,交抛物线于点,如图1中的和,
和是等底等高的两个三角
形,,
直线的解析式为,
联立方程组可得,
解得:或,
点或;
②当点在直线下方时,在的延长线上截取,过点作,交抛物线于点,如图1中的.
,
,且过点,
直线解析式为,联立方程组可得:,解得点,综上所述:点坐标为或,或;
(3)如图2,过点作,交于,设点,则点,,
当时,的面积有最大值,
点,再过点作,过点作于点,则,
当三点共线,且垂直时,最小,作于点,,MH即为所求的最小值,设与交于点,则又易得的最小值为.
458.【解】(1)将二次函数的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为,
点的坐标为,代入抛物线的解析式得,,
抛物线的解析式为:,
即.
令,解得,
,
的面积为,
,把代入抛物线解析式得:,解得:,
,设直线的解析式为,
把代入得:
解得:直线的解析式为.
(2)过点作轴交于,如图1,设,则,
,
,
,
当时,的面积有最大值,最大值是
此时点坐标为.
(3).作关于轴的对称点,连接交轴于点,
,
,
,
过点作于点,则.
,当E、P、Q三点共线,
且垂直时,有最小值,作⊥,则即为所求.
由三角形面积得:
,
,解得:
的最小值是3.
459.【解】(1)抛物线经过点,
,解得,
抛物线解析式为;
(2)如图1,连接,设点,其中,
四边形的面积为,由题意得
,
.
,开口向下,有最大值,当时,四边形的面积最大,此时,,
即.因此当四边形的面积最大时,点的坐标为.
解法二:连接,过点作轴的垂线,交于点,用铅垂定理也可.
(3),
顶点.如图2,连接交直线于点,
此时,的周长最小.设直线的解析式为,
且过点,解得:
直线的解析式为.在Rt中,.
为的中点,,
,
,
由图可知,设直线的函数解析式为,
把,代入得:,解得:
直线的解析式为.
联立得:,解得:,
.
460.【解】(1)将点的坐标代入二次函数表达式得:,解得:,
故抛物线的表达式为:;
(2)点轴,,
,
只有当时,,此时,即:
,设点的纵坐标为,则,
,将点坐标代入二次函数表达式并解得:(舍去)或,
则点);
(3)在Rt中,,
轴,RtRt,
,
而,
,
,即当取得最大值时,最大,
将坐标代入一次函数表达式并解得:直线的表达式为:,
设点,则点,
则,
当时,的最大值为4,故当时,
.
461.【解】(1)抛物线与轴交于点、可设交点式
把点代入得:
,
拋物线解析式为
(2)在拋物线的对称轴上存在一点,使得的周长最小.如图1,连接
点在抛物线对称轴直线上,点关于对称轴对称,
,
当在同一直线上时,最小,
,
由两点距离公式可得:
最小
设直线解析式为,把点代入得:,
解得:直线
点使的周长最小,最小值为.
(3)存在满足条件的点,使得.
当以为底时,两个三角形等高时,两个三角形面积相等,
点和点到直线距离相等时,,
现在,分两种情况讨论:
①若点在点上方,过点作,交抛物线于
点,如图2中的,
设直线解析式为
解得:直线
直线解析式为:,联立得:
解得:(即点,点坐标
②若点在点下方,如图3中的,
同理,,由题意可知,且直线到的距离等于直线到的距离,
直线向下平移2个单位得即为直线的解析式,联立得:
解得:或
点在轴上方
点坐标为
综上所述,点坐标为或
时,.
462.【解】(1)由拋物线交点式表达式得:,
,
即,解得:,
故抛物线的表达式为:;
(2)由抛物线的表达式知,点,
由点的坐标,得直线的表达式为:,
如图1,过点作轴,交直线于点,
设点,则点,
则
,
,
,
,
解得:或3(舍去1),故;
(3)当时,点,设点,点,则,①
第一种情况:当是边时,则的纵坐标为6或者一6,点向左平移2个单位向上平移6个单位得到点,同样点向左平移2个单位向上平移6个单位得到点,故或,
解得:或(不合题意的值已舍去);
故点的坐标为或或(2,0);
第二种情况:当是对角线时,由中点公式得:
③,
联立①③并解得,故点的坐标为,
综上,点的坐标为或,或或.
463.【解】(1),点,将点的坐标代入抛物线表达式:并解得:,故抛物线的表达式为:;
(2)如图,过点作轴于点,交于点,
,则,
,故,则,
由的坐标得:直线的表达式为:,设点,则点,,
解得:或2,故点或.
464.【解】(1)点,则抛物线的表达式为:,故,解得:,故抛物线的表达式为:(1),函数的对称轴为:;
(2)四边形的周长,其中是定值,故最小时,周长最小.
取点关于直线对称点,则
,取点,则,
故:,则当三点共线时,最小,周长也最小,
四边形的周长的最小值;
(3)设直线交轴于点,
直线把四边形的面积分为3:5两部分,
又
,则或,则或,
即:点的坐标为或,
将点的坐标代入直线的表达式:,
解得:或-2,
故直线的表达式为:或(2)
联立(1)(2)并解得:或8(不合题意值已舍去),
故点的坐标为或.
465.【解】(1)设二次函数的解析式为将点代入得,得二次函数的表达式为:
(2)依题意,点,点,设直线的解析式为,代入得,解得:线段所在的直线为,设点的坐标为:,则
,
,整理得,解得(舍去).故点的纵坐标为点的坐标为.
(3)存在满足条件的点,分两种情况讨论:(1).当点在轴的上方时,如图1,设直线交轴于,设,作于于.
由题意:,
,
,解得,
,由点,点可得:直线的解析式为,
联立方程组得:,解得或.
(2)当点在轴下方时,如图2,令,,解得:,
当点在的延长线上与抛物线的交点时,存在点使得,此时,的直线经过原点,设直线的解析式为,将点代入得:,故,则有整理得,,得(舍去),,当时,,故点为.
综上所述,点的坐标为或.
466.【解】(1)设抛物线的解析式为,在等腰Rt中,垂直平分,且,
,
,代入得:,解得,,
拋物线的解析式为;
(2)①设直线的解析式为,),由,可得,,
,
,
,
当时取最小值为4.此时直线1与轴重合,面积的最小值为4.
②假设抛物线上存在点,使得点与点关于直线对称,
,即,
解得,,
不合题意,舍去,当时,点,线段的中点为,代入得:,
直线的表达式为:
当时,点,线段的中点为,
代入得:,
直线的解析式为.
综上,点,直线解析式为
点,直线解析式为.
467.【解】(1)将点代入中,得:,
解得:,该拋物线表达式为.
(2)如图1,过点作轴,交于点,连接,
设点,则点,
,联立方程组:,
解得:,或,
点坐标为点的坐标为),
之间的水平宽度为
,(其中,
当时,的最大值为.
(3)分两种情况讨论:
①如图2,线段绕点逆时针旋转,得到线段,
设,
作轴于点轴于,
,,
,
在与中,,
,
,解得:,或,
,
②如图3,线段绕点顺时针旋转,得到线段,设,
作轴于点轴于,
,
线段绕点旋转,得到线段,
,
,
在与中,,
,
,解得:,
;
综上所述,点的坐标为,
.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第二十六节:二次函数面积问题
456.二次函数三角形面积最大值铅垂定理(初三)
如图,已知抛物线经过两点,且其对称轴为直线.
(1)求此拋物线的解析式;
(2)若点是抛物线上点与点之间的动点(不包括点,点),求的面积的最大值,并求出此时点的坐标.
457.二次函数面积相等动点问题胡不归最小值问题(初三)
如图,在平面直角坐标系中,已知直线与轴交于点,与轴交于点,过两点的抛物线与轴交于另一点.
(1)求抛物线的解析式;
(2)在抛物线上是否存在一点,使 若存在,请求出点的坐标,若不存在,请说明理由;
(3)点为直线下方抛物线上一点,点为轴上一点,当的面积最大时,求的最小值.
458.二次函数面积最大值问题胡不归最小值问题(初三)
在平面直角坐标系中,将二次函数)的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与轴交于点(点在点的左侧),,经过点的一次函数的图象与轴正半轴交于点,且与抛物线的另一个交点为的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点在一次函数的图象下方,求面积的最大值,并求出此时点的坐标;
(3)若点为轴上任意一点,在(2)的结论下,求的最小值.
459.二次函数面积最大值周长最小值求点的坐标(初三)
已知抛物线经过点,与轴交于点.
(1)求这条抛物线的解析式;
(2)如图1,点是第三象限内抛物线上的一个动点,当四边形的面积最大时,求点的坐标;
(3)如图2,线段的垂直平分线交轴于点,垂足为D,为抛物线的顶点,在直线上是否存在一点,使的周长最小 若存在,求出点的坐标;若不存在,请说明理由.
460.二次函数三角形相似存在性问题三角形面积最大值(初三)
如图,在平面直角坐标系中,抛物线与轴交于点,点,与轴交于点,连接.又已知位于轴右侧且垂直于轴的动直线1,沿轴正方向从0运动到(不含0点和点),且分别交抛物线、线段以及轴于点.
(1)求抛物线的表达式;
(2)连接,当直线1运动时,求使得和相似的点的坐标;
(3)作,垂足为,当直线1运动时,求面积的最大值.
461.二次函数将军饮马周长最小值面积相等问题(初三)
如图,抛物线的图象过点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点,使得的周长最小,若存在,请求出点的坐标及的周长;若不存在,请说明理由;
(3)在(2)的条件下,在轴上方的抛物线上是否存在点(不与点重合),使得 若存在,请求出点的坐标;若不存在,请说明理由.
462.二次函数面积倍分问题平行四边形存在性问题(初三)
如图,抛物线经过两点,与轴交于点,点是抛物线上一动点,设点的横坐标为,连接DC.
(1)求抛物线的函数表达式.
(2)当的面积等于的面积的时,求的值.
(3)当时,若点是轴上一动点,点是抛物线上一动点,试判断是否存在这样的点,使得以点为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
463.二次函数三角形面积倍分问题(初三)
如图,拖物线与轴交于点和点(点在原点的左侧,点在原点的右侧),与轴交于点.
(1)求该抛物线的函数解析式;
(2)连接,点是直线上方抛物线上的点,连接交于点,当时,求点的坐标.
464.二次函数造桥选址周长最小值面积倍分问题(初三)
如图抛物线经过点,点,且.
(1)求抛物线的解析式及其对称轴;
(2)如图1,点是直线上的两个动点,且,点在点的上方,求四边形ACDE的周长的最小值.
(3)如图2,点为抛物线上一点,连接,直线把四边形的面积分为两部分,求点的坐标.
465.线段相等求动点坐标二次函数面积倍分问题(初三)
如图,已知二次函数的图象与轴交于两点,为顶点,其中点的坐标为,点的坐标为.
(1)求该二次函数的表达式;
(2)点是线段上的一点,过点作轴的垂线,垂足为,且,求点的坐标.
(3)试问在该二次函数图象上是否存在点,使得的面积是的面积的若存在,求出点的坐标;若不存在,请说明理由.
466.二次函数面积最小值动点关于直线对称(初三)
在平面直角坐标系中,等腰直角的直角顶点在轴上,另两个顶点
在轴上,且,抛物线经过三点,如图1所示.
(1)求抛物线所表示的二次函数表达式.
(2)过原点任作直线1交抛物线于两点,如图2所示.
①求面积的最小值.
②已知是抛物线上一定点,问抛物线上是否存在点,使得点与点关于直线1对称,若存在,求出点的坐标及直线1的一次函数表达式;若不存在,请说明理由.
467.二次函数铅垂定理面积最大值线段旋转(初三)
在平面直角坐标系中,抛物线交轴于点,过点的直线交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点是直线下方抛物线上的一个动点(不与点重合),求面积的最大值;
(3)若点在抛物线上,将线段绕点0旋转,得到线段,是否存在点,使点恰好落在直线上 若存在,请直接写出点的坐标;若不存在,请说明理由.
答案
456.【解】(1)抛物线对称轴是直线且经过点,由抛物线的对称性可知:抛物线还经过点,,设抛物线的解析式为即:
把代入得:
抛物线的解析式为:.
(2)设直线的解析式为,直线为,
如图,作轴,交直线于,
设,则,
,此时,,
的面积的最大值为,
此时点的坐标为
457.【解】(1)直线与轴交于点,与轴交于点点,点,
点,点设抛物线解析式为:,
把点代入得:,
抛物线解析式为:;
(2)存在,分两种情况讨论:
①当点在直线上方时,过点作,交抛物线于点,如图1中的和,
和是等底等高的两个三角
形,,
直线的解析式为,
联立方程组可得,
解得:或,
点或;
②当点在直线下方时,在的延长线上截取,过点作,交抛物线于点,如图1中的.
,
,且过点,
直线解析式为,联立方程组可得:,解得点,综上所述:点坐标为或,或;
(3)如图2,过点作,交于,设点,则点,,
当时,的面积有最大值,
点,再过点作,过点作于点,则,
当三点共线,且垂直时,最小,作于点,,MH即为所求的最小值,设与交于点,则又易得的最小值为.
458.【解】(1)将二次函数的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为,
点的坐标为,代入抛物线的解析式得,,
抛物线的解析式为:,
即.
令,解得,
,
的面积为,
,把代入抛物线解析式得:,解得:,
,设直线的解析式为,
把代入得:
解得:直线的解析式为.
(2)过点作轴交于,如图1,设,则,
,
,
,
当时,的面积有最大值,最大值是
此时点坐标为.
(3).作关于轴的对称点,连接交轴于点,
,
,
,
过点作于点,则.
,当E、P、Q三点共线,
且垂直时,有最小值,作⊥,则即为所求.
由三角形面积得:
,
,解得:
的最小值是3.
459.【解】(1)抛物线经过点,
,解得,
抛物线解析式为;
(2)如图1,连接,设点,其中,
四边形的面积为,由题意得
,
.
,开口向下,有最大值,当时,四边形的面积最大,此时,,
即.因此当四边形的面积最大时,点的坐标为.
解法二:连接,过点作轴的垂线,交于点,用铅垂定理也可.
(3),
顶点.如图2,连接交直线于点,
此时,的周长最小.设直线的解析式为,
且过点,解得:
直线的解析式为.在Rt中,.
为的中点,,
,
,
由图可知,设直线的函数解析式为,
把,代入得:,解得:
直线的解析式为.
联立得:,解得:,
.
460.【解】(1)将点的坐标代入二次函数表达式得:,解得:,
故抛物线的表达式为:;
(2)点轴,,
,
只有当时,,此时,即:
,设点的纵坐标为,则,
,将点坐标代入二次函数表达式并解得:(舍去)或,
则点);
(3)在Rt中,,
轴,RtRt,
,
而,
,
,即当取得最大值时,最大,
将坐标代入一次函数表达式并解得:直线的表达式为:,
设点,则点,
则,
当时,的最大值为4,故当时,
.
461.【解】(1)抛物线与轴交于点、可设交点式
把点代入得:
,
拋物线解析式为
(2)在拋物线的对称轴上存在一点,使得的周长最小.如图1,连接
点在抛物线对称轴直线上,点关于对称轴对称,
,
当在同一直线上时,最小,
,
由两点距离公式可得:
最小
设直线解析式为,把点代入得:,
解得:直线
点使的周长最小,最小值为.
(3)存在满足条件的点,使得.
当以为底时,两个三角形等高时,两个三角形面积相等,
点和点到直线距离相等时,,
现在,分两种情况讨论:
①若点在点上方,过点作,交抛物线于
点,如图2中的,
设直线解析式为
解得:直线
直线解析式为:,联立得:
解得:(即点,点坐标
②若点在点下方,如图3中的,
同理,,由题意可知,且直线到的距离等于直线到的距离,
直线向下平移2个单位得即为直线的解析式,联立得:
解得:或
点在轴上方
点坐标为
综上所述,点坐标为或
时,.
462.【解】(1)由拋物线交点式表达式得:,
,
即,解得:,
故抛物线的表达式为:;
(2)由抛物线的表达式知,点,
由点的坐标,得直线的表达式为:,
如图1,过点作轴,交直线于点,
设点,则点,
则
,
,
,
,
解得:或3(舍去1),故;
(3)当时,点,设点,点,则,①
第一种情况:当是边时,则的纵坐标为6或者一6,点向左平移2个单位向上平移6个单位得到点,同样点向左平移2个单位向上平移6个单位得到点,故或,
解得:或(不合题意的值已舍去);
故点的坐标为或或(2,0);
第二种情况:当是对角线时,由中点公式得:
③,
联立①③并解得,故点的坐标为,
综上,点的坐标为或,或或.
463.【解】(1),点,将点的坐标代入抛物线表达式:并解得:,故抛物线的表达式为:;
(2)如图,过点作轴于点,交于点,
,则,
,故,则,
由的坐标得:直线的表达式为:,设点,则点,,
解得:或2,故点或.
464.【解】(1)点,则抛物线的表达式为:,故,解得:,故抛物线的表达式为:(1),函数的对称轴为:;
(2)四边形的周长,其中是定值,故最小时,周长最小.
取点关于直线对称点,则
,取点,则,
故:,则当三点共线时,最小,周长也最小,
四边形的周长的最小值;
(3)设直线交轴于点,
直线把四边形的面积分为3:5两部分,
又
,则或,则或,
即:点的坐标为或,
将点的坐标代入直线的表达式:,
解得:或-2,
故直线的表达式为:或(2)
联立(1)(2)并解得:或8(不合题意值已舍去),
故点的坐标为或.
465.【解】(1)设二次函数的解析式为将点代入得,得二次函数的表达式为:
(2)依题意,点,点,设直线的解析式为,代入得,解得:线段所在的直线为,设点的坐标为:,则
,
,整理得,解得(舍去).故点的纵坐标为点的坐标为.
(3)存在满足条件的点,分两种情况讨论:(1).当点在轴的上方时,如图1,设直线交轴于,设,作于于.
由题意:,
,
,解得,
,由点,点可得:直线的解析式为,
联立方程组得:,解得或.
(2)当点在轴下方时,如图2,令,,解得:,
当点在的延长线上与抛物线的交点时,存在点使得,此时,的直线经过原点,设直线的解析式为,将点代入得:,故,则有整理得,,得(舍去),,当时,,故点为.
综上所述,点的坐标为或.
466.【解】(1)设抛物线的解析式为,在等腰Rt中,垂直平分,且,
,
,代入得:,解得,,
拋物线的解析式为;
(2)①设直线的解析式为,),由,可得,,
,
,
,
当时取最小值为4.此时直线1与轴重合,面积的最小值为4.
②假设抛物线上存在点,使得点与点关于直线对称,
,即,
解得,,
不合题意,舍去,当时,点,线段的中点为,代入得:,
直线的表达式为:
当时,点,线段的中点为,
代入得:,
直线的解析式为.
综上,点,直线解析式为
点,直线解析式为.
467.【解】(1)将点代入中,得:,
解得:,该拋物线表达式为.
(2)如图1,过点作轴,交于点,连接,
设点,则点,
,联立方程组:,
解得:,或,
点坐标为点的坐标为),
之间的水平宽度为
,(其中,
当时,的最大值为.
(3)分两种情况讨论:
①如图2,线段绕点逆时针旋转,得到线段,
设,
作轴于点轴于,
,,
,
在与中,,
,
,解得:,或,
,
②如图3,线段绕点顺时针旋转,得到线段,设,
作轴于点轴于,
,
线段绕点旋转,得到线段,
,
,
在与中,,
,
,解得:,
;
综上所述,点的坐标为,
.
21世纪教育网(www.21cnjy.com)
同课章节目录
