【中考数学几何模型】第二十四节:二次函数相等角存在性问题438-447(含答案)
文档属性
| 名称 | 【中考数学几何模型】第二十四节:二次函数相等角存在性问题438-447(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-03 17:10:48 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中考数学几何模型
第二十四节:二次函数相等角存在性问题
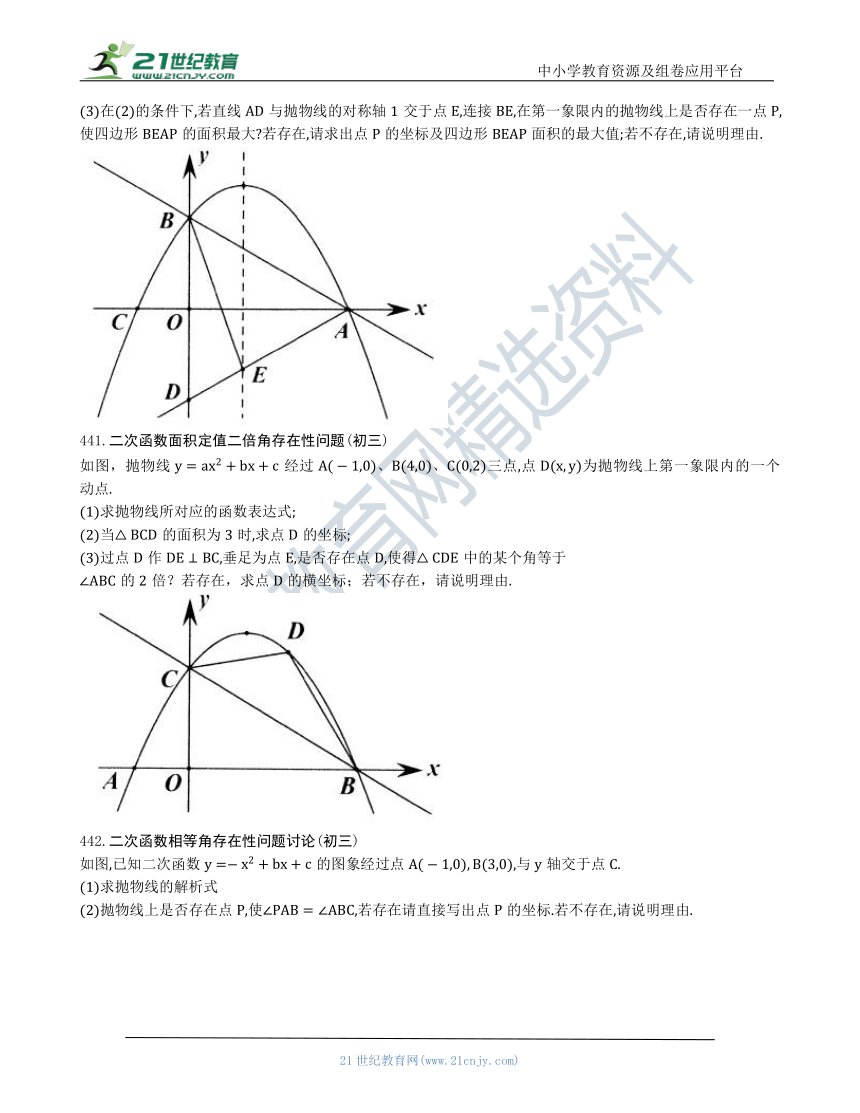
438.二次函数面积定值相等角存在性问题(初三)
如图,已知点在抛物线上.
(1)求抛物线解析式:
(2)在直线上方的抛物线上求一点,使面积为1;
(3)在轴下方且在抛物线对称轴上,是否存在一点,使 若存在,求出点坐标;若不存在,说明理由.
439.二次函数内心在轴上相等角存在性问题(初三)
如图,已知:抛物线与直线1交于点,与轴另一交点为.
(1)求抛物线的解析式
(2)在抛物线上找一点,使的内心在轴上,求点的坐标;
(3)是抛物线上一动点,过点作轴的垂线,垂足为,连接.在(2)的条件下,是否存在点,使 若存在,请求出点的坐标;若不存在,请说明理由.
440.二次函数角度相等四边形面积最大值(初三)
如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,点的坐标为,抛物线经过三点
(1)求抛物线的解析式;
(2)直线与轴负半轴交于点,且,求证:
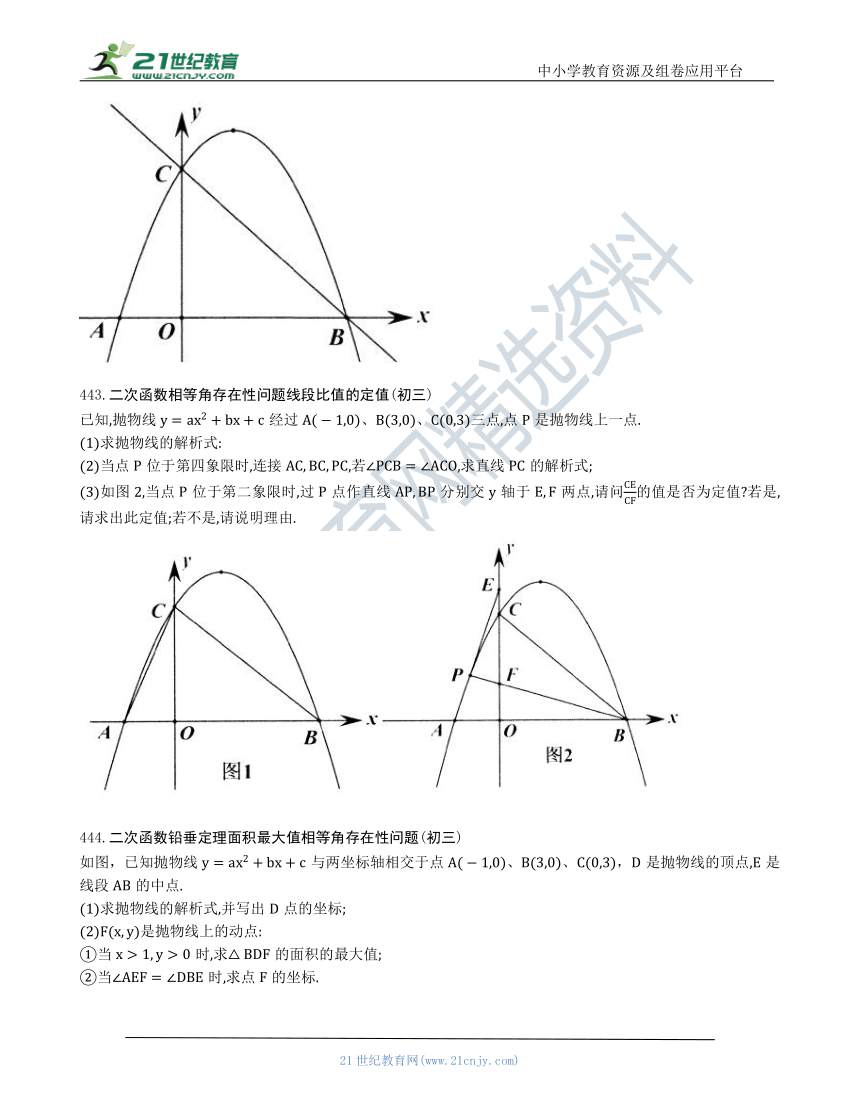
(3)在(2)的条件下,若直线与抛物线的对称轴1交于点,连接,在第一象限内的抛物线上是否存在一点,使四边形BEAP的面积最大 若存在,请求出点的坐标及四边形BEAP面积的最大值;若不存在,请说明理由.
441.二次函数面积定值二倍角存在性问题(初三)
如图,抛物线经过三点,点为抛物线上第一象限内的一个动点.
(1)求抛物线所对应的函数表达式;
(2)当的面积为3时,求点的坐标;
(3)过点作,垂足为点,是否存在点,使得中的某个角等于
的2倍?若存在,求点的横坐标;若不存在,请说明理由.
442.二次函数相等角存在性问题讨论(初三)
如图,已知二次函数的图象经过点,与y轴交于点C.
(1)求抛物线的解析式
(2)抛物线上是否存在点,使,若存在请直接写出点的坐标.若不存在,请说明理由.
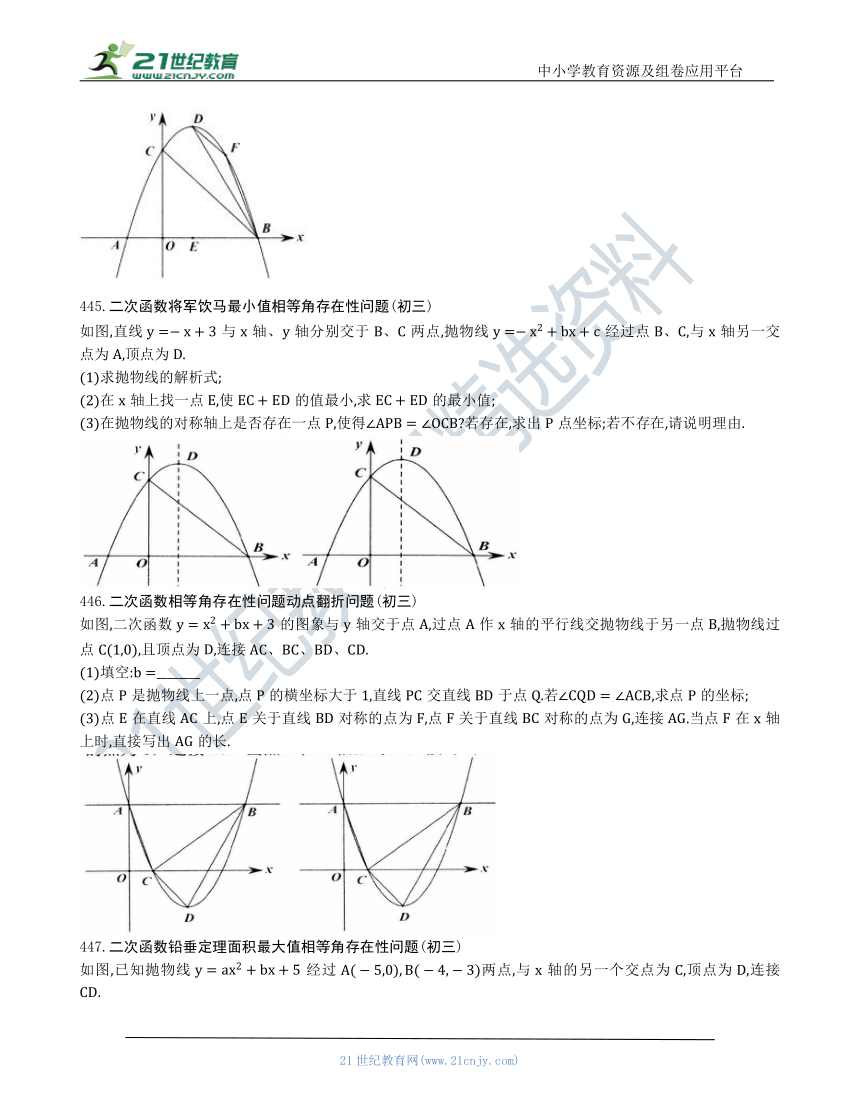
443.二次函数相等角存在性问题线段比值的定值(初三)
已知,抛物线经过三点,点是抛物线上一点.
(1)求抛物线的解析式:
(2)当点位于第四象限时,连接,若,求直线的解析式;
(3)如图2,当点位于第二象限时,过点作直线分别交y轴于两点,请问的值是否为定值 若是,请求出此定值;若不是,请说明理由.
444.二次函数铅垂定理面积最大值相等角存在性问题(初三)
如图,已知抛物线与两坐标轴相交于点、是抛物线的顶点,是线段的中点.
(1)求抛物线的解析式,并写出D点的坐标;
(2)是抛物线上的动点:
①当时,求的面积的最大值;
②当时,求点的坐标.
445.二次函数将军饮马最小值相等角存在性问题(初三)
如图,直线与轴、轴分别交于两点,抛物线经过点,与轴另一交点为,顶点为.
(1)求抛物线的解析式;
(2)在轴上找一点,使的值最小,求的最小值;
(3)在抛物线的对称轴上是否存在一点,使得 若存在,求出点坐标;若不存在,请说明理由.
446.二次函数相等角存在性问题动点翻折问题(初三)
如图,二次函数的图象与轴交于点,过点作轴的平行线交抛物线于另一点,拋物线过点,且顶点为,连接.
(1)填空:________
(2)点是抛物线上一点,点的横坐标大于1,直线交直线于点.若,求点的坐标;
(3)点在直线上,点关于直线对称的点为,点关于直线对称的点为,连接.当点在轴上时,直接写出的长.
447.二次函数铅垂定理面积最大值相等角存在性问题(初三)
如图,已知抛物线经过两点,与轴的另一个交点为C,顶点为D,连接CD.
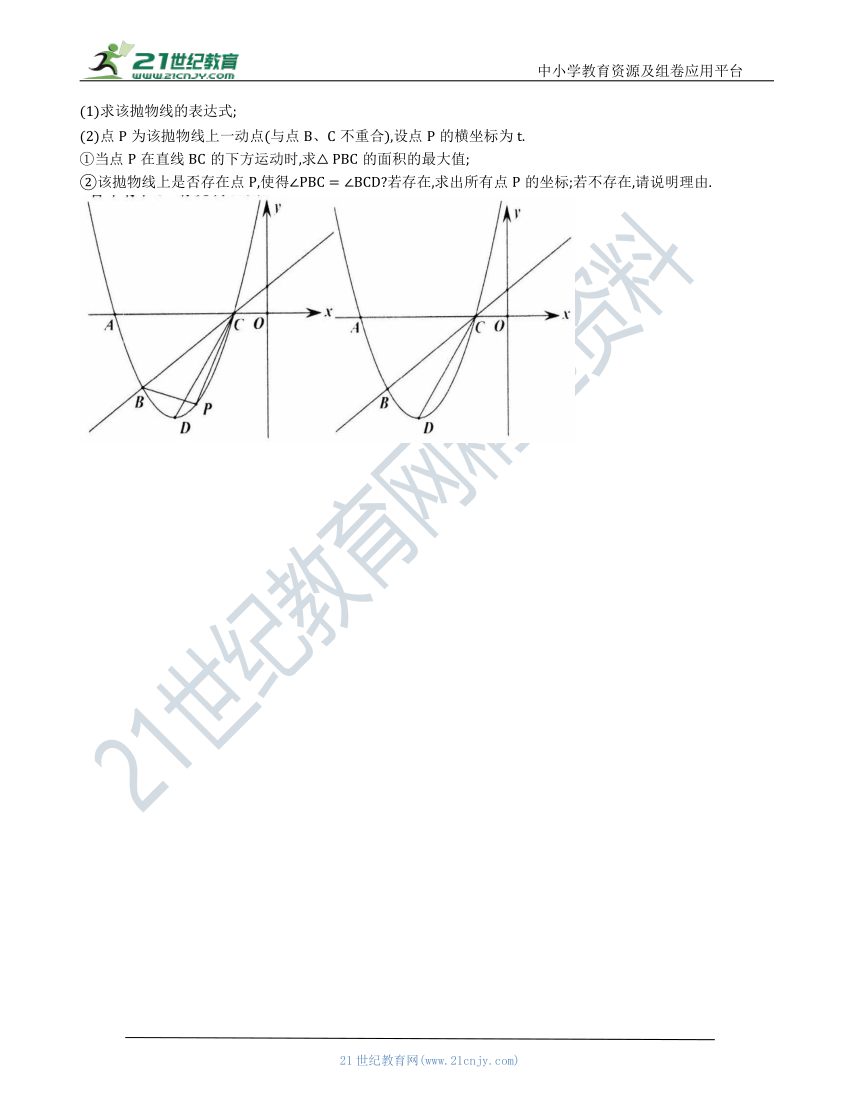
(1)求该抛物线的表达式;
(2)点为该拋物线上一动点(与点不重合),设点的横坐标为.
①当点在直线的下方运动时,求的面积的最大值;
②该拋物线上是否存在点,使得 若存在,求出所有点的坐标;若不存在,请说明理由.
答案
438【解】(1)设抛物线的解析式为,
将代入得,解得:,
拋物线的解析式为.
(2)如图,过点作,交于点.
设直线的解析式为,则,
解得:直线的解析式为.
设点,则
,
.
又,
整理得:,解得:或,
点的坐标为或.
(3)存在.作的外接圆,与轴下方对称轴的交点就是所求的点,连接,弦所对的圆周角相等,即.
.
,则.
设的半径为,则Rt中,由勾股定理可知,即,解得:(负值舍去),
的垂直平分线的为直线的垂直平分线为直线,
点为直线与的交点,即,
的坐标为.
439【解】(1)把点代入,得到方程组:,解得抛物线的解析式为;
(2)作点关于轴的对称点,则,连接并延长与抛物线交于点,由图形的对称性可知为所求的点,
设直线的解析式为,由题意得:,解得:,
直线的解析式为,
将直线和拋物线的解析式联立得:,
解得(舍去)或;
(3)存在点,理由如下:
已知,由两点距离公式可得:,
同理可求得,
,
,
,设点,
则,解得或,
当时,,
当,
综上所述,的坐标为.
440【解】(1)令,则,解得,
令,则,
设抛物线的解析式为,把三点坐标
代入解析式,得:,解得:,
抛物线的解析式为;
(2)证明:在平面直角坐标系中,
,
在和中,,
,
(3)存在,理由如下:如图,过点作轴于点,,
抛物线的对称轴是直线,
点的横坐标是2,即,,
,
设点的坐标为,
连接,过点作轴丁点,交直线于点,过点作于点,,
,
,
,抛物线开口向下,函数有最大值,
当时,面积的最大值是,此时四边形的面积最大,四边形BEAP的面积最大值为当点坐标是时,四边形面积的最大值是.
441【解】(1)将代入得:,
解得
故抛物线的解析式为.
(2)如图1,过作轴,与交于点,由可得直线的解析式为
,设
,解得:或3,
当时,,当时,,
点的坐标为或.
(3)存在,分两种情况考虑:
①当时,如图2,取点,
连接,
,
.
点直线的解析式为直线的解析式为.
联立直线及抛物线的解析式成方程组得:
,解得:(舍去),,
点的坐标为;
②当时,过点作于点,交于.作点关于的对称点,连接交于点,如图3所示.
∵,
在与中
∴∴即
.
设直线的解析式为,
:,解得,
直线的解析式为.
联立直线及直线成方程组得:,
解得:点的坐标为.
点,
直线的解析式为.
,且点直线的解析式为.联立直线及直线成方程组得:
,解得:,
点的坐标为点,点关于对称,点的坐标为.
点,
直线的解析式为.将代入:整理,得:,解得:(舍去)点的横坐标为.综上所述:存在点,使得的某个角恰好等于的2倍,点的横坐标为2或.
442.【解】(1)根据题意得,解得.故抛物线的解析式为;
(2)分两种情况,如图中的P1和P2:
①易知,二次函数的对称轴是直线,当时,,则,
点关于对称轴的对应点,
②时,满足题意,设直线的解析式为,则,解得.则直线的解析式为,设与平行的直线的解析式为,把代入得:则,解得.则与平行的直线的解析式为,联立拋物线解析式得:,解得(舍去)..综上所述,.
443.【解】(1)将代入,
(2)如图,过点作交于点,过点作轴交于点,,,,设直线的解析式为,直线的解析式为;
(3)的值是为定值.理由如下:
设,设直线的解析式为,把代入得:
,
直线AP的解析式为,
,
设直线的解析式为,把代入得:
,
直线BP的解析式为:,
,
的值是为定值.
444.【解】(1)将
代入,解得:,
抛物线的解析式为.
,
顶点的坐标为
(2)①过点作轴,交于点,如图1所示.设直线的解析式为,
将代入,
解得:直线的解析式为.
点的坐标为,
点的坐标为
,
.
当时,取最大值,最大值为1.
②过点作交轴于点,交抛物线于点,在轴负半轴取,连接,射线交抛物线于点,如图2,F1和足满足条件的点.
..
是线段的中点,,
点的坐标为.
设直线的解析式为,将代入,得,解得:,
直线的解析式为.
联立直线、抛物线解析式成方程组,,
解得:,或(舍去),
点的坐标为.
当时,点的坐标为,
点的坐标为.
同理,可求出直线的解析式为.
联立直线、抛物线解析式成方程组,,
解得:,或(舍去),
点的坐标为.
综上所述:当时,点的坐标为,或.
445.【解】(1)直线与轴、轴分别交于、两点,则点的坐标分别为,
将点的坐标代入二次函数表达式得:,
解得:,故抛物线的表达式为:,
(2)如图1,作点关于轴的对称点,连接交轴于点,则此时为最小,
抛物线的顶点坐标为,点,
将的坐标代入一次函数表达式并解得:
直线的表达式为:,当时,,
故点,由两点距离公式可得:,则的最小值为;
(3)设与对称轴交于点,则,以点为圆心,为半径作圆,交对称轴与点,此时就是轴上方,符合题意的点,作点关于轴的对称点,此时就是轴下方符合题意的点.易知是等腰直角三角形。易知,抛物线的对称轴是直线,
,同理:
综上所述,满足条件的点的坐标是:或者
446.【解】(1)抛物线的图象过点,故答案为:-4;
(2)抛物线解析式为
抛物线的图象与轴交于点,过点作轴的平行线交抛物线于另一点,
点,
点,
顶点坐标,
①当点在点上方时,如图1,过点作于,设与轴交于点,
点,点,点,
点,
,
,
点,点,点,
由两点距离公式得:
,
,
,
,
又点与点重合,
点是直线(即轴)与抛物线的交点,
点;
②当点在点下方时,如图2,过点作于,在线段的延长线上截取,连接交抛物线于点,
,
点,点,
直线解析式为:点,
直线解析式为:
解得:点坐标为,
,即是的中点,根据中点公式得,点直线解析式为:,联立方程组,解得:,或,点;
综上所述:点的坐标为或;
(3)如图3,设直线与的交点为,作于,过点作轴,过点作,连接,点,点,
直线解析式为:,点坐标为,
由(2)可知,点坐标为,
,
,
,点关于直线对称的点为,
,
又,,
点的横坐标是点的横坐标为,
点,
点关于直线对称的点
为,
点,
由两点距离公式可得:.
447.(1)将点坐标代入二次函数表达式得:,解得:,
故抛物线的表达式为:(1),
令,则或-5,即点;
(2)(1)如图1,过点作轴交于点,
由点坐标可得:直线的表达式为:(2),
设点,则点,
有最大值,
即当时,其最大值为;
(2)存在,现在分两种情况讨论:
第一种情况,当点在直线卜方时,如图2中的设直线与交于点,
点在的中垂线上,
线段的中点坐标为,
过该点与垂直的直线的值为-1,
设中垂线的表达式为:,将点
代入上式并解得:
直线中垂线的表达式为:(3),
同理直线的表达式为:(4),
联立(3)(4)并解得:,即点,
同理可得直线的表达式为:(5),
联立(1)(5)并解得:或-4,故点;
第2种情况,点在直线上方时,如图2中的,
,
则直线的表达式为:,
将点坐标代入上式并解得:,即直线的表达式为:(6),
联立(1)(6)并解得:或-4,故点;
故点的坐标为或.
21世纪教育网(www.21cnjy.com)
中考数学几何模型
第二十四节:二次函数相等角存在性问题
438.二次函数面积定值相等角存在性问题(初三)
如图,已知点在抛物线上.
(1)求抛物线解析式:
(2)在直线上方的抛物线上求一点,使面积为1;
(3)在轴下方且在抛物线对称轴上,是否存在一点,使 若存在,求出点坐标;若不存在,说明理由.
439.二次函数内心在轴上相等角存在性问题(初三)
如图,已知:抛物线与直线1交于点,与轴另一交点为.
(1)求抛物线的解析式
(2)在抛物线上找一点,使的内心在轴上,求点的坐标;
(3)是抛物线上一动点,过点作轴的垂线,垂足为,连接.在(2)的条件下,是否存在点,使 若存在,请求出点的坐标;若不存在,请说明理由.
440.二次函数角度相等四边形面积最大值(初三)
如图,在平面直角坐标系中,一次函数的图象与轴交于点,与轴交于点,点的坐标为,抛物线经过三点
(1)求抛物线的解析式;
(2)直线与轴负半轴交于点,且,求证:
(3)在(2)的条件下,若直线与抛物线的对称轴1交于点,连接,在第一象限内的抛物线上是否存在一点,使四边形BEAP的面积最大 若存在,请求出点的坐标及四边形BEAP面积的最大值;若不存在,请说明理由.
441.二次函数面积定值二倍角存在性问题(初三)
如图,抛物线经过三点,点为抛物线上第一象限内的一个动点.
(1)求抛物线所对应的函数表达式;
(2)当的面积为3时,求点的坐标;
(3)过点作,垂足为点,是否存在点,使得中的某个角等于
的2倍?若存在,求点的横坐标;若不存在,请说明理由.
442.二次函数相等角存在性问题讨论(初三)
如图,已知二次函数的图象经过点,与y轴交于点C.
(1)求抛物线的解析式
(2)抛物线上是否存在点,使,若存在请直接写出点的坐标.若不存在,请说明理由.
443.二次函数相等角存在性问题线段比值的定值(初三)
已知,抛物线经过三点,点是抛物线上一点.
(1)求抛物线的解析式:
(2)当点位于第四象限时,连接,若,求直线的解析式;
(3)如图2,当点位于第二象限时,过点作直线分别交y轴于两点,请问的值是否为定值 若是,请求出此定值;若不是,请说明理由.
444.二次函数铅垂定理面积最大值相等角存在性问题(初三)
如图,已知抛物线与两坐标轴相交于点、是抛物线的顶点,是线段的中点.
(1)求抛物线的解析式,并写出D点的坐标;
(2)是抛物线上的动点:
①当时,求的面积的最大值;
②当时,求点的坐标.
445.二次函数将军饮马最小值相等角存在性问题(初三)
如图,直线与轴、轴分别交于两点,抛物线经过点,与轴另一交点为,顶点为.
(1)求抛物线的解析式;
(2)在轴上找一点,使的值最小,求的最小值;
(3)在抛物线的对称轴上是否存在一点,使得 若存在,求出点坐标;若不存在,请说明理由.
446.二次函数相等角存在性问题动点翻折问题(初三)
如图,二次函数的图象与轴交于点,过点作轴的平行线交抛物线于另一点,拋物线过点,且顶点为,连接.
(1)填空:________
(2)点是抛物线上一点,点的横坐标大于1,直线交直线于点.若,求点的坐标;
(3)点在直线上,点关于直线对称的点为,点关于直线对称的点为,连接.当点在轴上时,直接写出的长.
447.二次函数铅垂定理面积最大值相等角存在性问题(初三)
如图,已知抛物线经过两点,与轴的另一个交点为C,顶点为D,连接CD.
(1)求该抛物线的表达式;
(2)点为该拋物线上一动点(与点不重合),设点的横坐标为.
①当点在直线的下方运动时,求的面积的最大值;
②该拋物线上是否存在点,使得 若存在,求出所有点的坐标;若不存在,请说明理由.
答案
438【解】(1)设抛物线的解析式为,
将代入得,解得:,
拋物线的解析式为.
(2)如图,过点作,交于点.
设直线的解析式为,则,
解得:直线的解析式为.
设点,则
,
.
又,
整理得:,解得:或,
点的坐标为或.
(3)存在.作的外接圆,与轴下方对称轴的交点就是所求的点,连接,弦所对的圆周角相等,即.
.
,则.
设的半径为,则Rt中,由勾股定理可知,即,解得:(负值舍去),
的垂直平分线的为直线的垂直平分线为直线,
点为直线与的交点,即,
的坐标为.
439【解】(1)把点代入,得到方程组:,解得抛物线的解析式为;
(2)作点关于轴的对称点,则,连接并延长与抛物线交于点,由图形的对称性可知为所求的点,
设直线的解析式为,由题意得:,解得:,
直线的解析式为,
将直线和拋物线的解析式联立得:,
解得(舍去)或;
(3)存在点,理由如下:
已知,由两点距离公式可得:,
同理可求得,
,
,
,设点,
则,解得或,
当时,,
当,
综上所述,的坐标为.
440【解】(1)令,则,解得,
令,则,
设抛物线的解析式为,把三点坐标
代入解析式,得:,解得:,
抛物线的解析式为;
(2)证明:在平面直角坐标系中,
,
在和中,,
,
(3)存在,理由如下:如图,过点作轴于点,,
抛物线的对称轴是直线,
点的横坐标是2,即,,
,
设点的坐标为,
连接,过点作轴丁点,交直线于点,过点作于点,,
,
,
,抛物线开口向下,函数有最大值,
当时,面积的最大值是,此时四边形的面积最大,四边形BEAP的面积最大值为当点坐标是时,四边形面积的最大值是.
441【解】(1)将代入得:,
解得
故抛物线的解析式为.
(2)如图1,过作轴,与交于点,由可得直线的解析式为
,设
,解得:或3,
当时,,当时,,
点的坐标为或.
(3)存在,分两种情况考虑:
①当时,如图2,取点,
连接,
,
.
点直线的解析式为直线的解析式为.
联立直线及抛物线的解析式成方程组得:
,解得:(舍去),,
点的坐标为;
②当时,过点作于点,交于.作点关于的对称点,连接交于点,如图3所示.
∵,
在与中
∴∴即
.
设直线的解析式为,
:,解得,
直线的解析式为.
联立直线及直线成方程组得:,
解得:点的坐标为.
点,
直线的解析式为.
,且点直线的解析式为.联立直线及直线成方程组得:
,解得:,
点的坐标为点,点关于对称,点的坐标为.
点,
直线的解析式为.将代入:整理,得:,解得:(舍去)点的横坐标为.综上所述:存在点,使得的某个角恰好等于的2倍,点的横坐标为2或.
442.【解】(1)根据题意得,解得.故抛物线的解析式为;
(2)分两种情况,如图中的P1和P2:
①易知,二次函数的对称轴是直线,当时,,则,
点关于对称轴的对应点,
②时,满足题意,设直线的解析式为,则,解得.则直线的解析式为,设与平行的直线的解析式为,把代入得:则,解得.则与平行的直线的解析式为,联立拋物线解析式得:,解得(舍去)..综上所述,.
443.【解】(1)将代入,
(2)如图,过点作交于点,过点作轴交于点,,,,设直线的解析式为,直线的解析式为;
(3)的值是为定值.理由如下:
设,设直线的解析式为,把代入得:
,
直线AP的解析式为,
,
设直线的解析式为,把代入得:
,
直线BP的解析式为:,
,
的值是为定值.
444.【解】(1)将
代入,解得:,
抛物线的解析式为.
,
顶点的坐标为
(2)①过点作轴,交于点,如图1所示.设直线的解析式为,
将代入,
解得:直线的解析式为.
点的坐标为,
点的坐标为
,
.
当时,取最大值,最大值为1.
②过点作交轴于点,交抛物线于点,在轴负半轴取,连接,射线交抛物线于点,如图2,F1和足满足条件的点.
..
是线段的中点,,
点的坐标为.
设直线的解析式为,将代入,得,解得:,
直线的解析式为.
联立直线、抛物线解析式成方程组,,
解得:,或(舍去),
点的坐标为.
当时,点的坐标为,
点的坐标为.
同理,可求出直线的解析式为.
联立直线、抛物线解析式成方程组,,
解得:,或(舍去),
点的坐标为.
综上所述:当时,点的坐标为,或.
445.【解】(1)直线与轴、轴分别交于、两点,则点的坐标分别为,
将点的坐标代入二次函数表达式得:,
解得:,故抛物线的表达式为:,
(2)如图1,作点关于轴的对称点,连接交轴于点,则此时为最小,
抛物线的顶点坐标为,点,
将的坐标代入一次函数表达式并解得:
直线的表达式为:,当时,,
故点,由两点距离公式可得:,则的最小值为;
(3)设与对称轴交于点,则,以点为圆心,为半径作圆,交对称轴与点,此时就是轴上方,符合题意的点,作点关于轴的对称点,此时就是轴下方符合题意的点.易知是等腰直角三角形。易知,抛物线的对称轴是直线,
,同理:
综上所述,满足条件的点的坐标是:或者
446.【解】(1)抛物线的图象过点,故答案为:-4;
(2)抛物线解析式为
抛物线的图象与轴交于点,过点作轴的平行线交抛物线于另一点,
点,
点,
顶点坐标,
①当点在点上方时,如图1,过点作于,设与轴交于点,
点,点,点,
点,
,
,
点,点,点,
由两点距离公式得:
,
,
,
,
又点与点重合,
点是直线(即轴)与抛物线的交点,
点;
②当点在点下方时,如图2,过点作于,在线段的延长线上截取,连接交抛物线于点,
,
点,点,
直线解析式为:点,
直线解析式为:
解得:点坐标为,
,即是的中点,根据中点公式得,点直线解析式为:,联立方程组,解得:,或,点;
综上所述:点的坐标为或;
(3)如图3,设直线与的交点为,作于,过点作轴,过点作,连接,点,点,
直线解析式为:,点坐标为,
由(2)可知,点坐标为,
,
,
,点关于直线对称的点为,
,
又,,
点的横坐标是点的横坐标为,
点,
点关于直线对称的点
为,
点,
由两点距离公式可得:.
447.(1)将点坐标代入二次函数表达式得:,解得:,
故抛物线的表达式为:(1),
令,则或-5,即点;
(2)(1)如图1,过点作轴交于点,
由点坐标可得:直线的表达式为:(2),
设点,则点,
有最大值,
即当时,其最大值为;
(2)存在,现在分两种情况讨论:
第一种情况,当点在直线卜方时,如图2中的设直线与交于点,
点在的中垂线上,
线段的中点坐标为,
过该点与垂直的直线的值为-1,
设中垂线的表达式为:,将点
代入上式并解得:
直线中垂线的表达式为:(3),
同理直线的表达式为:(4),
联立(3)(4)并解得:,即点,
同理可得直线的表达式为:(5),
联立(1)(5)并解得:或-4,故点;
第2种情况,点在直线上方时,如图2中的,
,
则直线的表达式为:,
将点坐标代入上式并解得:,即直线的表达式为:(6),
联立(1)(6)并解得:或-4,故点;
故点的坐标为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
