河南省濮阳市综合高中数学(人教版)必修三课件:312 概率的意义(共17张PPT)
文档属性
| 名称 | 河南省濮阳市综合高中数学(人教版)必修三课件:312 概率的意义(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-04 15:52:40 | ||
图片预览






文档简介
课件17张PPT。3.1.2 概率的意义zxxk 学习目标(1)正确理解概率的意义;
(2)利用概率知识正确理解现实生活中的实际问题.
(3)通过对现实生活中的“掷币”、“游戏的公平性”、“彩票中奖”等问题的探究,感知应用数学知识解决数学问题的方法,理解逻辑推理的数学方法. 一、概率的意义思考1:有人说,既然抛掷一枚硬币出现正面向上的概率为0.5,那么连续抛掷一枚硬币两次,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗?
答: 这种想法显然是错误的,通过具体的试验可以发现有三种可能的结果:“两次正面朝上”“两次反面朝上”“一次正面朝上,一次反面朝上”,而且其概率分别为:0.25, 0.25,0.5. 上面的问题告诉我们,随机事件在一次试验中发生与否是随机的,但随机中含有规律性,认识了这种随机性的规律性,可以帮助我们准确预测随机事件发生的可能性.思考2:如果某种彩票中奖的概率为 ,那么买1000张彩票一定能中奖吗?
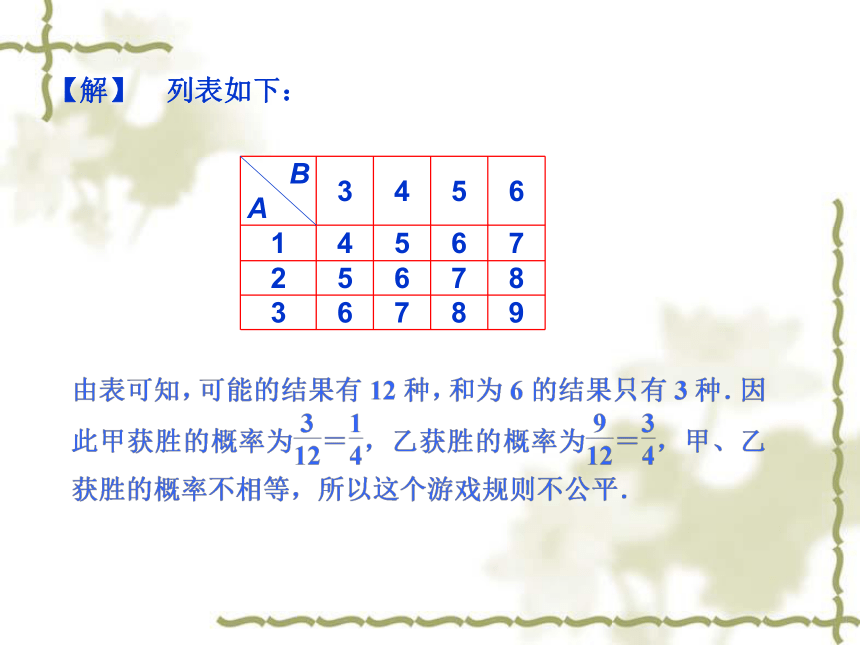
答:不一定能中奖,因为买1000张彩票相当于做1000次试验,因为每次试验的结果都是随机的,即每张彩票可能中奖也可能不中奖,因此,1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖. 思考:在足球比赛中,裁判员有时用抛硬币的方法来决定谁先发球,其规则是:事先规定两队谁代表正面谁代表反面,硬币落地后向上的一面为发球方.你认为这个规则公平吗?答:规则是公平的. 因为两个队取得发球权的概率都是0.5.二、游戏的公平性zxxk训练1:如图所示,有两个可以自由转动的均匀转盘A,B,转盘A被平均分成3等份,分别标上1,2,3三个数字;转盘B被平均分成4等份,分别标上3,4,5,6四个数字.现为甲、乙两人设计游戏规则:自由转动转盘A和B,转盘停止后,指针指上一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则乙获胜,你认为这个规则公平吗?【解】 列表如下:答:我们面临两种可能的决策: 一种是这枚骰子的质地均匀;
另一种是这枚骰子的质地不均匀. 如果连续10次掷一枚骰子,
结果都是出现1点, 这时我们更愿意接受第二种情况,这枚骰
子靠近6点的那面比较重,这样更有可能出现10个1点.三、决策中的概率思想
思考:如果连续10次掷一枚骰子,结果都是出现1点.你认为这枚骰子的质地均匀吗?为什么?分析:利用刚学过的概率知识可知出现各个面的可能性都应该是 ,当连续10次投掷这枚骰子,结果都是 出现1点的概率为( )10≈0.0000000016538. 当我们面临从多个可选答案中挑选正确答案的决策时,如果按照“发生的可能性最大”作为决策的准则而做出判断,这种判断问题的方法称为“极大似然法”,极大似然法是统计中重要的统计思想方法之一。 训练2:
有一个转盘游戏,转盘被平均分成10
等份(如图所示),转动转盘,当转盘停
止后,指针指向的数字即为转出的数字.
游戏规则如下:两个人参加,先确定猜
数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍数”或“不是4的整数倍数”.zxxk请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
四、天气预报的概率解释 思考:“天气预报说昨天本地降水的概率为90%,结果一滴雨都没下,天气预报也太不准确了.” 学了概率后,你能给出解释吗?答:天气预报的“降水”是一个随机事件,概率为90%指明了“降水”这个随机事件发生的概率,我们知道:在一次试验中,概率为90%的事件也可能不出现,因此,“昨天没有下雨”并不说明“昨天的降水概率为90%”的天气预报是错误的. 五、孟德尔的遗传学与概率 阅读课本117—118 的内容.了解孟德尔与遗传学.训练3: 某水产试验厂实行某种鱼的人工孵化,10000个鱼卵能孵出8513尾鱼苗,根据概率的统计定义解答下列问题: (1)求这种鱼卵的孵化率; (2)30000个鱼卵大约能孵化多少尾鱼苗? (3)要孵化5000尾鱼苗,大概得准备多少鱼卵(精确到百位)解:(1)这种鱼卵的孵化频率为 =0.8513,它近似的为孵化的概率?.
(2)设能孵化x个,则, ∴x=25539,
即30000个鱼卵大约能孵化25539尾鱼苗.
(3)设需备y个鱼卵,则, ∴y≈5873,
即大概得准备5873个鱼卵. 课堂练习1、课本118页练习1、2、3.
2、在天气预报中,“明天降水的概率为85%”是指( )
A.明天该地区有85%的时间降水,其他时间不降水;
B.明天该地区有85%的地区降水,其他15%的地区不降水;
C,在气象台专家中,有85%的专家认为该地区明天会降水;
D.明天该地区降水的可能性微85%.
3、老师讲一道数学题,某同学能听懂的概率是0.8,是指( )
A.老师每讲一道题,他有80%的部分能听懂;
B.老师讲10道题,他能听懂8道;
C.他能听懂老师所讲这道题的可能性为80%;
D.以上解释都不对.DC4、据河南省教育研究机构统计,今年在校中学生近视率约为37.4%,某配镜商要到某中学给学生配镜,若该学校学生人数是600人,则配镜商应带眼睛数目为( )
A.347副. B.224副.
C.不少于225副. D.不多于225副.C 课堂小结 概率是一门研究现实世界中广泛存在的随机现象的科学,正确理解概率的意义是认识、理解现实生活中有关概率的实例的关键,学习过程中应有意识形成概率意识,并用这种意识来理解现实世界,主动参与对事件发生的概率的感受和探索.通过以上例题与练习可以感到,数学特别是概率正越来越多地应用到我们的生活当中.它们已经不是数学家手中的抽象理论,而成为我们认识世界的工具.从彩票中奖,到证券分析;从基因工程,到法律诉讼;从市场调查,到经济宏观调控,概率无处不在. 本部分内容讲解结束再 见!zxxk
(2)利用概率知识正确理解现实生活中的实际问题.
(3)通过对现实生活中的“掷币”、“游戏的公平性”、“彩票中奖”等问题的探究,感知应用数学知识解决数学问题的方法,理解逻辑推理的数学方法. 一、概率的意义思考1:有人说,既然抛掷一枚硬币出现正面向上的概率为0.5,那么连续抛掷一枚硬币两次,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗?
答: 这种想法显然是错误的,通过具体的试验可以发现有三种可能的结果:“两次正面朝上”“两次反面朝上”“一次正面朝上,一次反面朝上”,而且其概率分别为:0.25, 0.25,0.5. 上面的问题告诉我们,随机事件在一次试验中发生与否是随机的,但随机中含有规律性,认识了这种随机性的规律性,可以帮助我们准确预测随机事件发生的可能性.思考2:如果某种彩票中奖的概率为 ,那么买1000张彩票一定能中奖吗?
答:不一定能中奖,因为买1000张彩票相当于做1000次试验,因为每次试验的结果都是随机的,即每张彩票可能中奖也可能不中奖,因此,1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖. 思考:在足球比赛中,裁判员有时用抛硬币的方法来决定谁先发球,其规则是:事先规定两队谁代表正面谁代表反面,硬币落地后向上的一面为发球方.你认为这个规则公平吗?答:规则是公平的. 因为两个队取得发球权的概率都是0.5.二、游戏的公平性zxxk训练1:如图所示,有两个可以自由转动的均匀转盘A,B,转盘A被平均分成3等份,分别标上1,2,3三个数字;转盘B被平均分成4等份,分别标上3,4,5,6四个数字.现为甲、乙两人设计游戏规则:自由转动转盘A和B,转盘停止后,指针指上一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则乙获胜,你认为这个规则公平吗?【解】 列表如下:答:我们面临两种可能的决策: 一种是这枚骰子的质地均匀;
另一种是这枚骰子的质地不均匀. 如果连续10次掷一枚骰子,
结果都是出现1点, 这时我们更愿意接受第二种情况,这枚骰
子靠近6点的那面比较重,这样更有可能出现10个1点.三、决策中的概率思想
思考:如果连续10次掷一枚骰子,结果都是出现1点.你认为这枚骰子的质地均匀吗?为什么?分析:利用刚学过的概率知识可知出现各个面的可能性都应该是 ,当连续10次投掷这枚骰子,结果都是 出现1点的概率为( )10≈0.0000000016538. 当我们面临从多个可选答案中挑选正确答案的决策时,如果按照“发生的可能性最大”作为决策的准则而做出判断,这种判断问题的方法称为“极大似然法”,极大似然法是统计中重要的统计思想方法之一。 训练2:
有一个转盘游戏,转盘被平均分成10
等份(如图所示),转动转盘,当转盘停
止后,指针指向的数字即为转出的数字.
游戏规则如下:两个人参加,先确定猜
数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:
A.猜“是奇数”或“是偶数”;
B.猜“是4的整数倍数”或“不是4的整数倍数”.zxxk请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你会选哪种猜数方案?
(2)为了保证游戏的公平性,你认为应选哪种猜数方案?
四、天气预报的概率解释 思考:“天气预报说昨天本地降水的概率为90%,结果一滴雨都没下,天气预报也太不准确了.” 学了概率后,你能给出解释吗?答:天气预报的“降水”是一个随机事件,概率为90%指明了“降水”这个随机事件发生的概率,我们知道:在一次试验中,概率为90%的事件也可能不出现,因此,“昨天没有下雨”并不说明“昨天的降水概率为90%”的天气预报是错误的. 五、孟德尔的遗传学与概率 阅读课本117—118 的内容.了解孟德尔与遗传学.训练3: 某水产试验厂实行某种鱼的人工孵化,10000个鱼卵能孵出8513尾鱼苗,根据概率的统计定义解答下列问题: (1)求这种鱼卵的孵化率; (2)30000个鱼卵大约能孵化多少尾鱼苗? (3)要孵化5000尾鱼苗,大概得准备多少鱼卵(精确到百位)解:(1)这种鱼卵的孵化频率为 =0.8513,它近似的为孵化的概率?.
(2)设能孵化x个,则, ∴x=25539,
即30000个鱼卵大约能孵化25539尾鱼苗.
(3)设需备y个鱼卵,则, ∴y≈5873,
即大概得准备5873个鱼卵. 课堂练习1、课本118页练习1、2、3.
2、在天气预报中,“明天降水的概率为85%”是指( )
A.明天该地区有85%的时间降水,其他时间不降水;
B.明天该地区有85%的地区降水,其他15%的地区不降水;
C,在气象台专家中,有85%的专家认为该地区明天会降水;
D.明天该地区降水的可能性微85%.
3、老师讲一道数学题,某同学能听懂的概率是0.8,是指( )
A.老师每讲一道题,他有80%的部分能听懂;
B.老师讲10道题,他能听懂8道;
C.他能听懂老师所讲这道题的可能性为80%;
D.以上解释都不对.DC4、据河南省教育研究机构统计,今年在校中学生近视率约为37.4%,某配镜商要到某中学给学生配镜,若该学校学生人数是600人,则配镜商应带眼睛数目为( )
A.347副. B.224副.
C.不少于225副. D.不多于225副.C 课堂小结 概率是一门研究现实世界中广泛存在的随机现象的科学,正确理解概率的意义是认识、理解现实生活中有关概率的实例的关键,学习过程中应有意识形成概率意识,并用这种意识来理解现实世界,主动参与对事件发生的概率的感受和探索.通过以上例题与练习可以感到,数学特别是概率正越来越多地应用到我们的生活当中.它们已经不是数学家手中的抽象理论,而成为我们认识世界的工具.从彩票中奖,到证券分析;从基因工程,到法律诉讼;从市场调查,到经济宏观调控,概率无处不在. 本部分内容讲解结束再 见!zxxk
