河南省濮阳市综合高中数学(人教版)必修五课件:34基本不等式(共22张PPT)
文档属性
| 名称 | 河南省濮阳市综合高中数学(人教版)必修五课件:34基本不等式(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-04 15:55:00 | ||
图片预览





文档简介
课件22张PPT。基本不等式复习 授课人:王洪山zxxk 考试大纲 (一) 了解基本不等式的证明过程。
(二) 会用基本不等式 解决简单的最值问题
考情分析 1.基本不等式的考查以理解和灵活应用为主,应用基本不等式求最值是考查的重点。
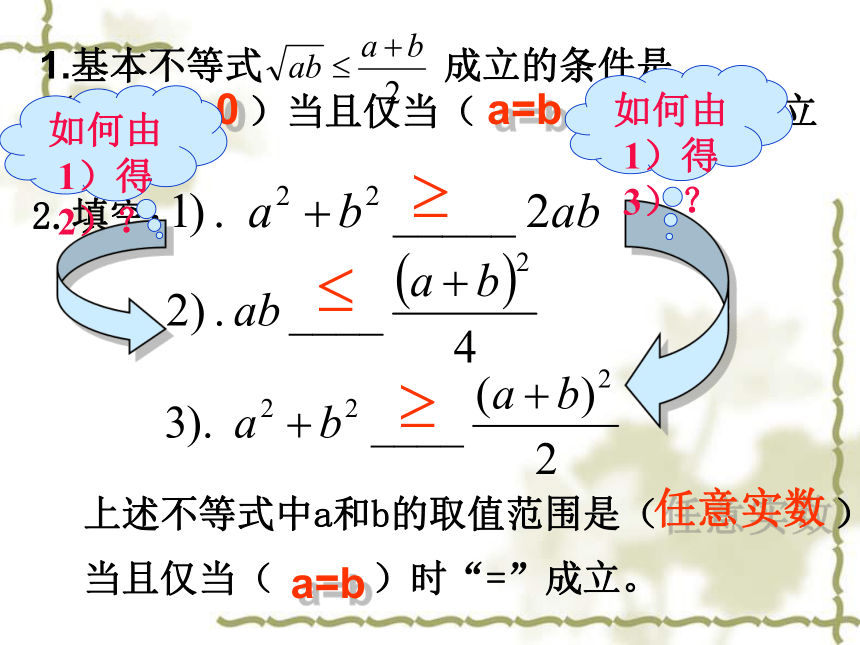
2.考查分为两个方面:一是直接利用基本不等式 求最值。二是用配凑法进行恒等变形后求最值。 3.试题多以选择题、填空题为主,多属中档题目,有时也会与其他知识结合出现在解答题中,分值一般为5分。学习目标 1.能够直接利用基本不等式求最值 2.能掌握变形过程中常用的一些方法和技巧 3.树立分类讨论的思想意识。任意实数a=ba>0,b>0a=b1.基本不等式 成立的条件是
( )当且仅当( )时“=”成立2.填空:上述不等式中a和b的取值范围是( ),
当且仅当( )时“=”成立。zxxk3.已知a>0,b>0,则
(1)如果积ab是定值p,由 那么
当且仅当_____时,a+b 有最___值是______.
(2)如果和a+b是定值p,由 那么
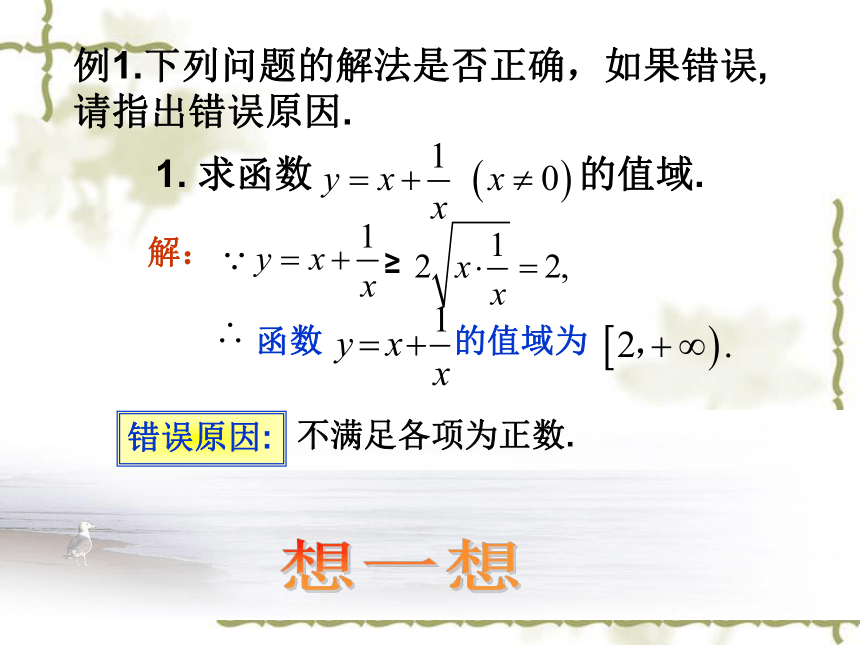
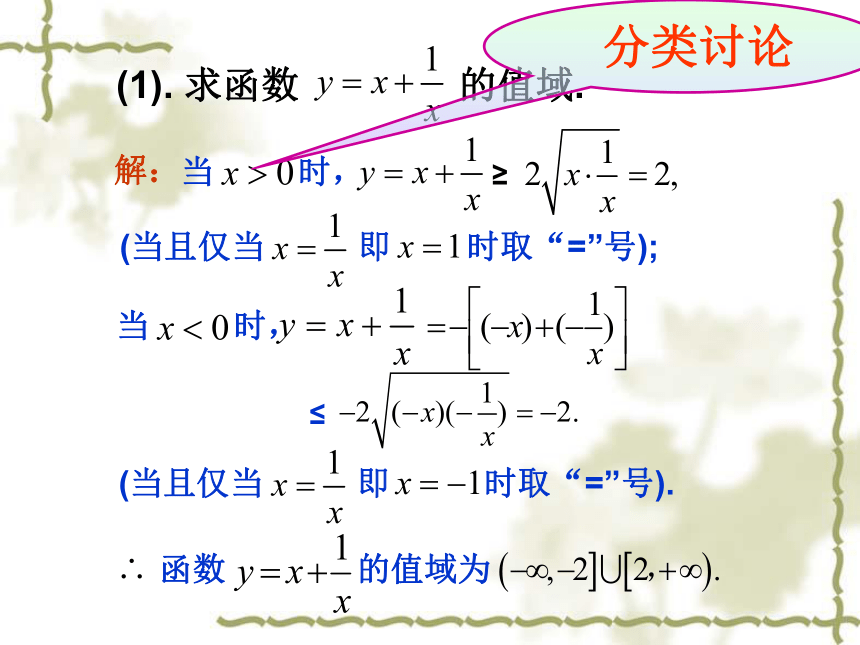
当且仅当____时,ab有最 ____值是______.大a=b小a=b 积定和最小, 和定积最大。 1. 求函数 的值域.解:≥例1.下列问题的解法是否正确,如果错误, 请指出错误原因.函数 的值域为想一想(1). 求函数 的值域. 分类讨论解:解: 改变系数,凑成和为定值解:≥函数的最小值为 . 应用基本不等式求最值需要注意:
一正二定三相等【例2】求下列各题的最值.
(1)x>3,求 的最小值;
(2)x>1,求 的最小值;zxxk 改变常数项,凑成积为定值 凑定值所以函数的最小值为7
(2)x>1,求 的最小值;解析: 分离常数,拆项凑成积为定值凑定值 条件最值的求法例3.求下列函数的最值解析:当且仅当“=”成立“1”的整体代换,凑成定值多次运用基本不等式时,必须保证“=”同时成立解析:当且仅当a+b=a+c时“=”成立方法总结:对条件等式进行因式分解的恒等变形后,出现定值
练一练A 2. 已知x> ,则函数y= 的最小值是( )53.已知t>0, 则 的最小值为( )
-21.基本不等式及其变形,3.凑定值时常用的变形方法。课堂小结2. 应用基本不等式求最值需要注意的问 题,(3). 求函数 的最小值.解:≥函数的最小值为 .拓展探究?请写出正确解法zxxk布置作业金版新学案97页 再见! 谢 谢 参 与
(二) 会用基本不等式 解决简单的最值问题
考情分析 1.基本不等式的考查以理解和灵活应用为主,应用基本不等式求最值是考查的重点。
2.考查分为两个方面:一是直接利用基本不等式 求最值。二是用配凑法进行恒等变形后求最值。 3.试题多以选择题、填空题为主,多属中档题目,有时也会与其他知识结合出现在解答题中,分值一般为5分。学习目标 1.能够直接利用基本不等式求最值 2.能掌握变形过程中常用的一些方法和技巧 3.树立分类讨论的思想意识。任意实数a=ba>0,b>0a=b1.基本不等式 成立的条件是
( )当且仅当( )时“=”成立2.填空:上述不等式中a和b的取值范围是( ),
当且仅当( )时“=”成立。zxxk3.已知a>0,b>0,则
(1)如果积ab是定值p,由 那么
当且仅当_____时,a+b 有最___值是______.
(2)如果和a+b是定值p,由 那么
当且仅当____时,ab有最 ____值是______.大a=b小a=b 积定和最小, 和定积最大。 1. 求函数 的值域.解:≥例1.下列问题的解法是否正确,如果错误, 请指出错误原因.函数 的值域为想一想(1). 求函数 的值域. 分类讨论解:解: 改变系数,凑成和为定值解:≥函数的最小值为 . 应用基本不等式求最值需要注意:
一正二定三相等【例2】求下列各题的最值.
(1)x>3,求 的最小值;
(2)x>1,求 的最小值;zxxk 改变常数项,凑成积为定值 凑定值所以函数的最小值为7
(2)x>1,求 的最小值;解析: 分离常数,拆项凑成积为定值凑定值 条件最值的求法例3.求下列函数的最值解析:当且仅当“=”成立“1”的整体代换,凑成定值多次运用基本不等式时,必须保证“=”同时成立解析:当且仅当a+b=a+c时“=”成立方法总结:对条件等式进行因式分解的恒等变形后,出现定值
练一练A 2. 已知x> ,则函数y= 的最小值是( )53.已知t>0, 则 的最小值为( )
-21.基本不等式及其变形,3.凑定值时常用的变形方法。课堂小结2. 应用基本不等式求最值需要注意的问 题,(3). 求函数 的最小值.解:≥函数的最小值为 .拓展探究?请写出正确解法zxxk布置作业金版新学案97页 再见! 谢 谢 参 与
