河南省濮阳市综合高中数学(人教版)必修一课件:212指数函数(共17张PPT)
文档属性
| 名称 | 河南省濮阳市综合高中数学(人教版)必修一课件:212指数函数(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 157.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-04 18:55:01 | ||
图片预览






文档简介
课件17张PPT。§3 指数函数zxxk学习导航
学习目标
重点难点
重点:指数函数的图像与性质.
难点:指数函数中底数a的变化对函数值变化的影响.
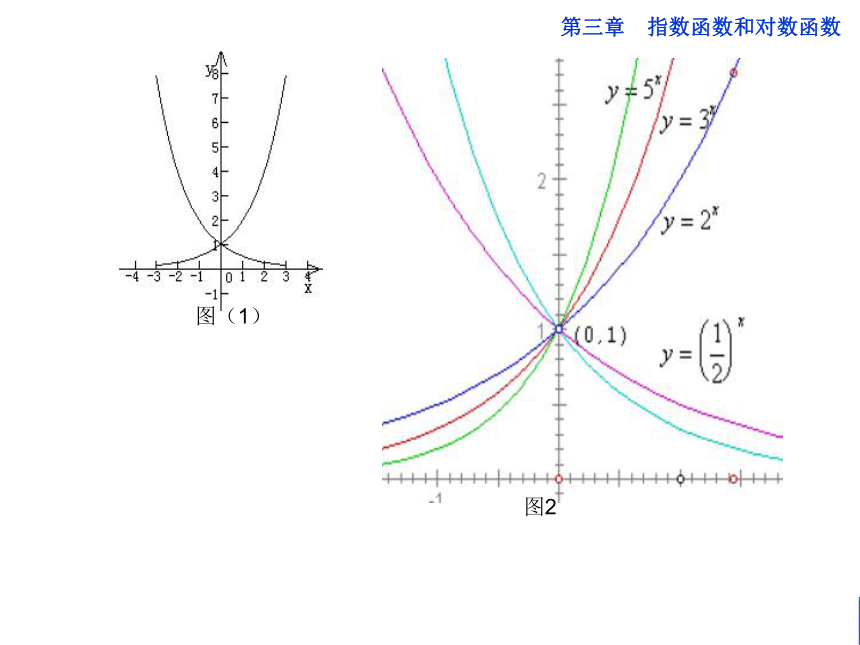
1、请在同一坐标系画出 和 的图像,并说出他们的相同点和不同点,从中你能得到什么结论。
2、请你在同一坐标系中画出函数 和 的图像,并说出他们的相同点和不同点。
3、指数函数的定义:且,函数 且a≠1) 的定义域是实数集R.你能画出指数函数(a>0且a≠1)的图象吗?应该是什么样的呢?请同学们探讨一下.1.指数函数的概念
函数y=ax(a>0且a≠1,x∈R)叫作指数函
数,在这个函数中,自变量x出现在指数的位置上,底数a是一个大于0且不等于1的常量,函数的定义域是实数集R.
做一做
1.下列函数是指数函数的是( )
A.y=(-3)x B.y=-3x
C.y=32x D.y=2x+1
解析:选C.32x=(32)x=9x是指数函数.
2.指数函数y=ax(a>0,a≠1,x∈R)的图像与性质
(0,1)01y>10<y<10<y<1y>1增函数减函数非奇非偶zxxk做一做
2.函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D想一想练习比较下列各题中两个数的大小: 和 方法一:直接用科学计算器计算各数的值,再对两个数值进行大小比较。
方法二:利用指数函数的性质对两个数值进行大小比较。1 求下列函数的定义域 和
解:指数函数的定义域为R,所以 的定
义域为R,而函数 要有意义
需使得3-X>0所以其定义域为X≤32已知指数函数 (a>0且a≠1)经过点(3,π)求f(0),f(3),f(-3)的值
分析:我们知道函数图象经过某个点,那么这个点的坐标就满足这个函数的方程。zxxk小结学习了指数函数的概念及图象和性质;可以利用性质比较两个指数的大小
作业
习题3.3 第1,2题补充习题1在同一坐标系画出下列函数图象,并说出它们间的关系,并总结出一般的结论:
和 和
2求函数 的定义域
3若指数函数 在(-∞,+∞)是减函数,求a的范围
学习目标
重点难点
重点:指数函数的图像与性质.
难点:指数函数中底数a的变化对函数值变化的影响.
1、请在同一坐标系画出 和 的图像,并说出他们的相同点和不同点,从中你能得到什么结论。
2、请你在同一坐标系中画出函数 和 的图像,并说出他们的相同点和不同点。
3、指数函数的定义:且,函数 且a≠1) 的定义域是实数集R.你能画出指数函数(a>0且a≠1)的图象吗?应该是什么样的呢?请同学们探讨一下.1.指数函数的概念
函数y=ax(a>0且a≠1,x∈R)叫作指数函
数,在这个函数中,自变量x出现在指数的位置上,底数a是一个大于0且不等于1的常量,函数的定义域是实数集R.
做一做
1.下列函数是指数函数的是( )
A.y=(-3)x B.y=-3x
C.y=32x D.y=2x+1
解析:选C.32x=(32)x=9x是指数函数.
2.指数函数y=ax(a>0,a≠1,x∈R)的图像与性质
(0,1)01y>10<y<10<y<1y>1增函数减函数非奇非偶zxxk做一做
2.函数y=15x的图像是( )
解析:选B.x=0,y=1,且为增函数.
答案:D想一想练习比较下列各题中两个数的大小: 和 方法一:直接用科学计算器计算各数的值,再对两个数值进行大小比较。
方法二:利用指数函数的性质对两个数值进行大小比较。1 求下列函数的定义域 和
解:指数函数的定义域为R,所以 的定
义域为R,而函数 要有意义
需使得3-X>0所以其定义域为X≤32已知指数函数 (a>0且a≠1)经过点(3,π)求f(0),f(3),f(-3)的值
分析:我们知道函数图象经过某个点,那么这个点的坐标就满足这个函数的方程。zxxk小结学习了指数函数的概念及图象和性质;可以利用性质比较两个指数的大小
作业
习题3.3 第1,2题补充习题1在同一坐标系画出下列函数图象,并说出它们间的关系,并总结出一般的结论:
和 和
2求函数 的定义域
3若指数函数 在(-∞,+∞)是减函数,求a的范围
