河南省濮阳市综合高中数学(人教版)选修2-1课件:221椭圆的标准方程(共14张PPT)
文档属性
| 名称 | 河南省濮阳市综合高中数学(人教版)选修2-1课件:221椭圆的标准方程(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-04 00:00:00 | ||
图片预览



文档简介
课件14张PPT。椭圆的标准方程(第一课时) 濮阳市综合高中
吴河岭
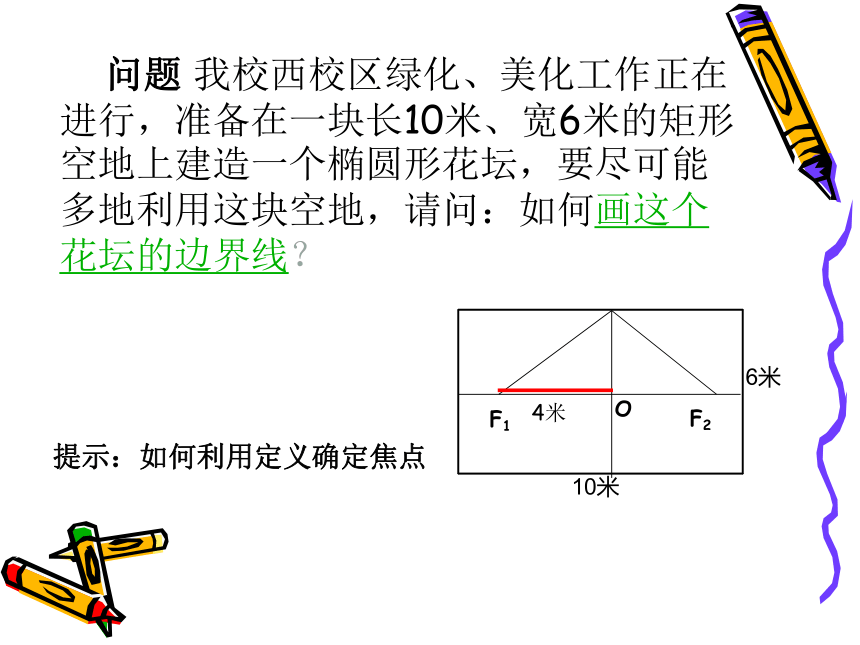
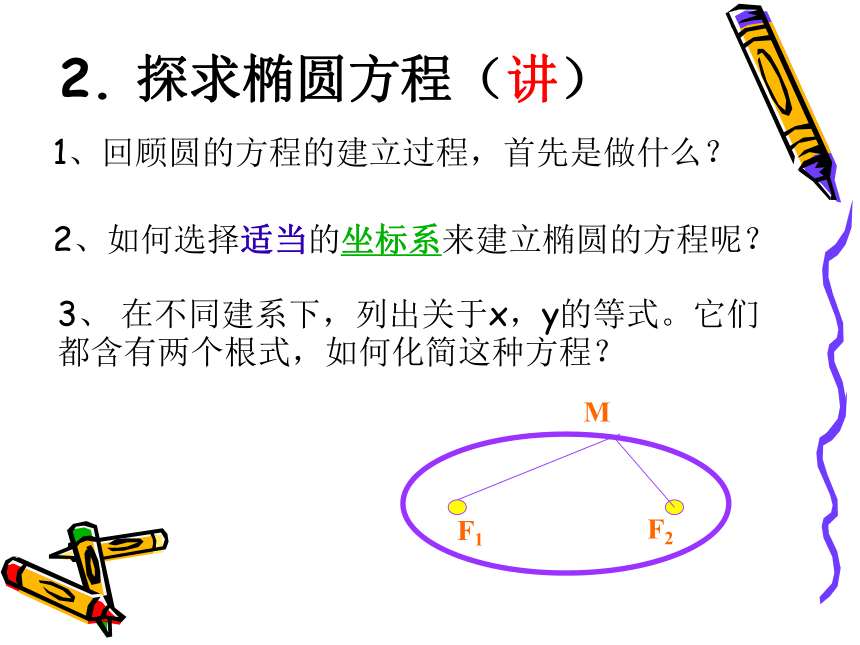
zxxk学习目标①会建立直角坐标系,根据椭圆的定义 建立椭圆的标准方程,②能根据已知条件求椭圆的标准方程,情境 请同学们举出生活中椭圆形物体的实例1. 创设问题情境( )学 问题 我校西校区绿化、美化工作正在进行,准备在一块长10米、宽6米的矩形空地上建造一个椭圆形花坛,要尽可能多地利用这块空地,请问:如何画这个花坛的边界线?4米F1F2O提示:如何利用定义确定焦点2. 探求椭圆方程(讲)1、回顾圆的方程的建立过程,首先是做什么?2、如何选择适当的坐标系来建立椭圆的方程呢?
3、 在不同建系下,列出关于x,y的等式。它们
都含有两个根式,如何化简这种方程?对比一下
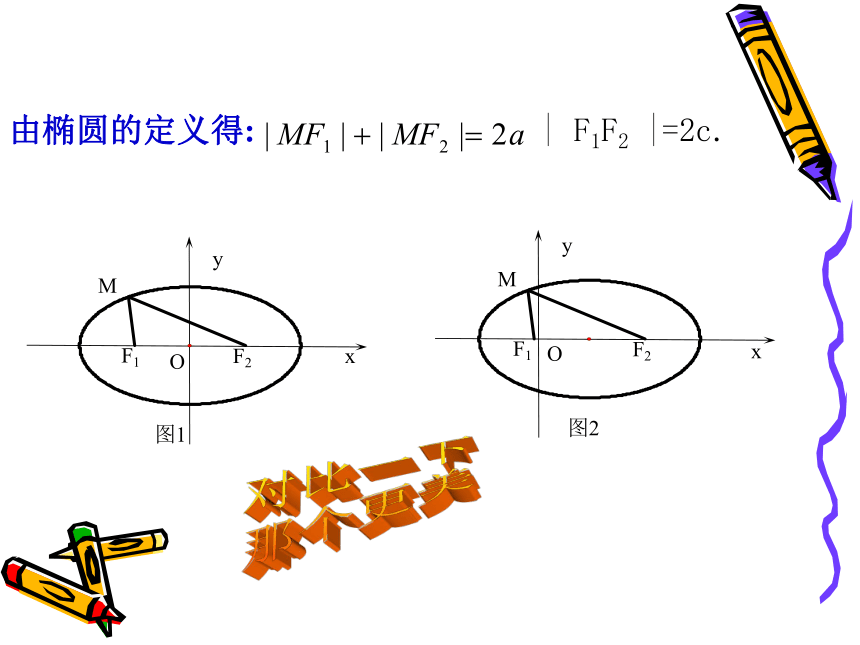
那个更美由椭圆的定义得:| F1F2 |=2c.zxxk 解法一:以两定点F1、F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得代入坐标得方程 (a>b>0)两边再平方,得整理得移项,再平方由上述过程可知,椭圆上的点的坐标(x,y)都满足上面这个方程;满足这个方程的点(x,y)都在已知的椭圆上。所以,这个方程就是所求得椭圆的方程.法二 以两定点F1、F2所在直线为x轴,F1为原点,建立直角坐标系(如图2).
设M(x,y)为椭圆上的任意一点, | F1F2 |=2c.
设F1、F2的坐标分别是(0,0)、(2c,0) .类似第一种方法,整理可得通过比较可知,(a>b>0)更简洁。由得方程(1)建系——建立适当的坐标系思考:如果椭圆竖起放置,怎样建系?
建立如图所示的直角坐标系,类似于刚才的
推导过程可得椭圆的方程,同学们课后完成。曲线相对于坐标轴有较多的对称性移项后
再平方推导椭圆的标准方程的步骤:我们把方程(a>b>0)叫做椭圆的标准方程。(a>b>0),猜一猜 ?
与前面方程有什么关系(2)设点(3)列式(4)化简(5)证明①方程中x,y表示椭圆上任意一点的坐标;
②关于x,y的二元二次方程;
③方程右边是常数1,左边是平方和的形式;
④a是椭圆上的点到两焦点距离和的一半,b2=a2-c2,c是焦距的一半, a>b>0, a>c>0,b与c大小不定
⑤焦点位置的判定:焦点在较大分母对应的变量的坐标轴上 3. 标准方程比较(1)相同点(2)不同点
4.初步运用知识(练)则 a=___,b=___,c=___,焦点坐标为 ,与坐标轴交点坐标为 ,焦距等于 ;如果点P为该椭圆上一点,则PF1+PF2=__ __( F1,F2为焦点).1定位 、 2定量、 3待定系数法 5.课堂小结1).推导椭圆的标准方程2). 椭圆两种标准方程的比较3).椭圆的标准方程的基本求法及应用4).自主探索,合作交流点拨总结:(2)已知椭圆的方程为(1)若椭圆的焦距为8,a=5,那么它的标准方程是6.课后作业布置1).基础训练题:课本P28 1. 2.2).动手操作题:课本P29 7(或用几何画板探求)3).课后思考题:有关资料显示:“神舟六号”飞船的运行轨道是以地球的中心F2位一个焦点的椭圆。已知它的近地点A(离地面最近的点)距地面200公里,远地点B (离地面最远的点) 距地面347公里,并且在F2、A、B同一直线上,地球半径约为6371km。你能计算出“神舟六号”飞船的轨道方程吗? (精确到0.01 km)谢谢大家!zxxk
吴河岭
zxxk学习目标①会建立直角坐标系,根据椭圆的定义 建立椭圆的标准方程,②能根据已知条件求椭圆的标准方程,情境 请同学们举出生活中椭圆形物体的实例1. 创设问题情境( )学 问题 我校西校区绿化、美化工作正在进行,准备在一块长10米、宽6米的矩形空地上建造一个椭圆形花坛,要尽可能多地利用这块空地,请问:如何画这个花坛的边界线?4米F1F2O提示:如何利用定义确定焦点2. 探求椭圆方程(讲)1、回顾圆的方程的建立过程,首先是做什么?2、如何选择适当的坐标系来建立椭圆的方程呢?
3、 在不同建系下,列出关于x,y的等式。它们
都含有两个根式,如何化简这种方程?对比一下
那个更美由椭圆的定义得:| F1F2 |=2c.zxxk 解法一:以两定点F1、F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得代入坐标得方程 (a>b>0)两边再平方,得整理得移项,再平方由上述过程可知,椭圆上的点的坐标(x,y)都满足上面这个方程;满足这个方程的点(x,y)都在已知的椭圆上。所以,这个方程就是所求得椭圆的方程.法二 以两定点F1、F2所在直线为x轴,F1为原点,建立直角坐标系(如图2).
设M(x,y)为椭圆上的任意一点, | F1F2 |=2c.
设F1、F2的坐标分别是(0,0)、(2c,0) .类似第一种方法,整理可得通过比较可知,(a>b>0)更简洁。由得方程(1)建系——建立适当的坐标系思考:如果椭圆竖起放置,怎样建系?
建立如图所示的直角坐标系,类似于刚才的
推导过程可得椭圆的方程,同学们课后完成。曲线相对于坐标轴有较多的对称性移项后
再平方推导椭圆的标准方程的步骤:我们把方程(a>b>0)叫做椭圆的标准方程。(a>b>0),猜一猜 ?
与前面方程有什么关系(2)设点(3)列式(4)化简(5)证明①方程中x,y表示椭圆上任意一点的坐标;
②关于x,y的二元二次方程;
③方程右边是常数1,左边是平方和的形式;
④a是椭圆上的点到两焦点距离和的一半,b2=a2-c2,c是焦距的一半, a>b>0, a>c>0,b与c大小不定
⑤焦点位置的判定:焦点在较大分母对应的变量的坐标轴上 3. 标准方程比较(1)相同点(2)不同点
4.初步运用知识(练)则 a=___,b=___,c=___,焦点坐标为 ,与坐标轴交点坐标为 ,焦距等于 ;如果点P为该椭圆上一点,则PF1+PF2=__ __( F1,F2为焦点).1定位 、 2定量、 3待定系数法 5.课堂小结1).推导椭圆的标准方程2). 椭圆两种标准方程的比较3).椭圆的标准方程的基本求法及应用4).自主探索,合作交流点拨总结:(2)已知椭圆的方程为(1)若椭圆的焦距为8,a=5,那么它的标准方程是6.课后作业布置1).基础训练题:课本P28 1. 2.2).动手操作题:课本P29 7(或用几何画板探求)3).课后思考题:有关资料显示:“神舟六号”飞船的运行轨道是以地球的中心F2位一个焦点的椭圆。已知它的近地点A(离地面最近的点)距地面200公里,远地点B (离地面最远的点) 距地面347公里,并且在F2、A、B同一直线上,地球半径约为6371km。你能计算出“神舟六号”飞船的轨道方程吗? (精确到0.01 km)谢谢大家!zxxk
