河南省濮阳市综合高中数学(人教版)选修2-2课件:31复数的几何意义(共15张PPT)
文档属性
| 名称 | 河南省濮阳市综合高中数学(人教版)选修2-2课件:31复数的几何意义(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-04 18:56:37 | ||
图片预览






文档简介
课件15张PPT。§3.1复数的几何意义综合高中 邱爱珍zxxk课前复习 1 、 指出下列复数的实部和虚部。
0,( -2)i, 3+2i, -22、 实数m分别取什么数值时, 复数z=(m+3)+(3-m)i
为(1)实数,(2)虚数,(3)纯虚数复数的几何意义(一)
问题情境一
(1)复数的几何意义是什么?为什么?
(2)什么是复平面?什么是实轴?什么是虚
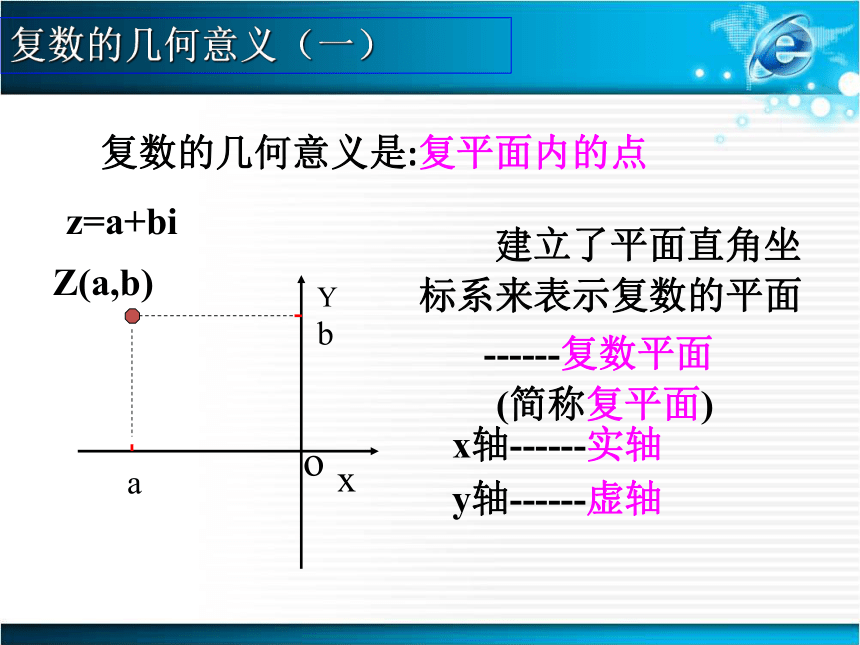
轴?xYobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴------复数平面 (简称复平面)z=a+bi复数的几何意义(一)复数的几何意义是:复平面内的点反馈训练: 1指出下列复平面内的点对应的复数。DCFEOBAXYF: -3iA: 2+5iB: -3+2iC: 2-4iD: -3-5i复数的几何意义(一)zxxk反馈训练2:指出下列复数所对应的点的坐标0, 2, 2+i, i,复数的几何意义(一)解: (0,0),3:下列命题中的假命题是( ) (A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,实轴上的点所对应的复数都是实数;
(C)在复平面内,虚轴上的点所对应的复数都是纯虚数。
(D)在复平面内,对应于纯虚数的点都在虚轴上;
总结:在复平面内,虚轴上的点(除原点外)所对应的复数都是纯虚数。(0,1)(2,1),(2,0),C例1 已知复数z=(m2+3m-10)+(m2+m-12)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 复数的几何意义(一)合作探究解: 因为z对应的点在第二象限总结:表示复数的点所在象限的问题即是复数的实部与虚部所满足的不等式组的问题。总结:十字相乘法,配方法,求根公式法。及解一元二次不等式的步骤问题情境(二)
1 还有什么量也可以用坐标来表示?
2复数Z=a+bi的模(绝对值)如何定义?
3复数Z=a+bi的模(绝对值)的几何意义是什 么?
4实数 的绝对值的几何意义是什么?
5实数的绝对值与复数的模这两个概念的区别与联系是什么?复数的几何意义(二)复数z=a+bi复平面内的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bi小结yxOZ=a+biZ (a,b)小结复数的模(绝对值)?zxxk 例2:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai( 5 )( 5 )复数的模(绝对值)总结:复数的模其实是实数绝对值概念的推广复数的模的几何意义:复数的模(绝对值)高考链接1(2010北京卷2)在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( )
(A)4+8i (B)8+2i (C)2+4i (D)4+i2.(2009北京卷理1)在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限CB课堂小结1、复数的几何意义;
2、复数的模(绝对值);
布置作业教材P55 3,4,5zxxk
0,( -2)i, 3+2i, -22、 实数m分别取什么数值时, 复数z=(m+3)+(3-m)i
为(1)实数,(2)虚数,(3)纯虚数复数的几何意义(一)
问题情境一
(1)复数的几何意义是什么?为什么?
(2)什么是复平面?什么是实轴?什么是虚
轴?xYobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴------复数平面 (简称复平面)z=a+bi复数的几何意义(一)复数的几何意义是:复平面内的点反馈训练: 1指出下列复平面内的点对应的复数。DCFEOBAXYF: -3iA: 2+5iB: -3+2iC: 2-4iD: -3-5i复数的几何意义(一)zxxk反馈训练2:指出下列复数所对应的点的坐标0, 2, 2+i, i,复数的几何意义(一)解: (0,0),3:下列命题中的假命题是( ) (A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,实轴上的点所对应的复数都是实数;
(C)在复平面内,虚轴上的点所对应的复数都是纯虚数。
(D)在复平面内,对应于纯虚数的点都在虚轴上;
总结:在复平面内,虚轴上的点(除原点外)所对应的复数都是纯虚数。(0,1)(2,1),(2,0),C例1 已知复数z=(m2+3m-10)+(m2+m-12)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 复数的几何意义(一)合作探究解: 因为z对应的点在第二象限总结:表示复数的点所在象限的问题即是复数的实部与虚部所满足的不等式组的问题。总结:十字相乘法,配方法,求根公式法。及解一元二次不等式的步骤问题情境(二)
1 还有什么量也可以用坐标来表示?
2复数Z=a+bi的模(绝对值)如何定义?
3复数Z=a+bi的模(绝对值)的几何意义是什 么?
4实数 的绝对值的几何意义是什么?
5实数的绝对值与复数的模这两个概念的区别与联系是什么?复数的几何意义(二)复数z=a+bi复平面内的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义(二)xyobaZ(a,b)z=a+bi小结yxOZ=a+biZ (a,b)小结复数的模(绝对值)?zxxk 例2:求下列复数的模:
(1)z1=-5i
(2)z2=-3+4i
(3)z3=5-5i (4)z4=1+mi(m∈R)
(5)z5=4a-3ai( 5 )( 5 )复数的模(绝对值)总结:复数的模其实是实数绝对值概念的推广复数的模的几何意义:复数的模(绝对值)高考链接1(2010北京卷2)在复平面内,复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( )
(A)4+8i (B)8+2i (C)2+4i (D)4+i2.(2009北京卷理1)在复平面内,复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限CB课堂小结1、复数的几何意义;
2、复数的模(绝对值);
布置作业教材P55 3,4,5zxxk
