青岛版数学七年级上册 5.5 函数的初步认识 课件(共17张PPT)
文档属性
| 名称 | 青岛版数学七年级上册 5.5 函数的初步认识 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 00:10:02 | ||
图片预览




文档简介
(共17张PPT)
第5章 代数式与函数的初步认识
5.5 函数的初步认识
学习目标
结合实例,了解并能够区分自变量、函数值与函数
对于给定的函数,能根据自变量的值求出函数的值
能根据实际问题列出函数表达式,也能利用函数表达式解决实际问题
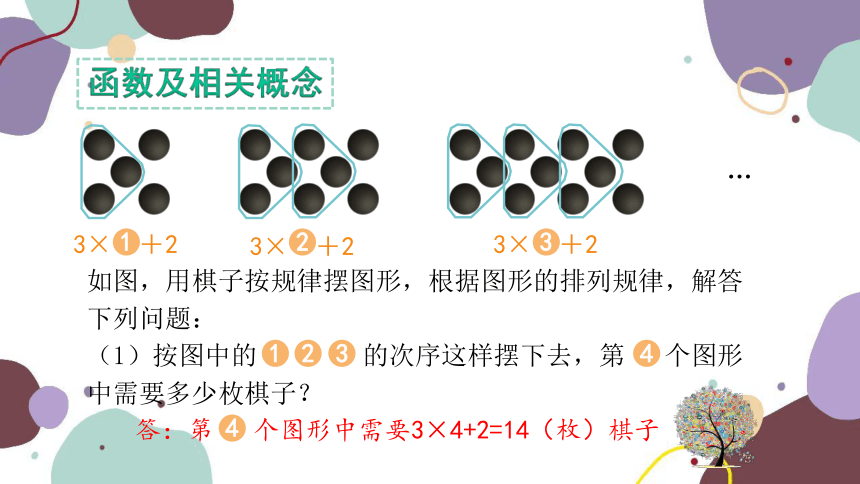
3× +2
3× +2
3× +2
函数及相关概念
如图,用棋子按规律摆图形,根据图形的排列规律,解答下列问题:
1
2
3
…
(1)按图中的 的次序这样摆下去,第 个图形中需要多少枚棋子?
1
2
3
4
答:第 个图形中需要3×4+2=14(枚)棋子
4
3× +2
3× +2
3× +2
3× +2
1
2
3
…
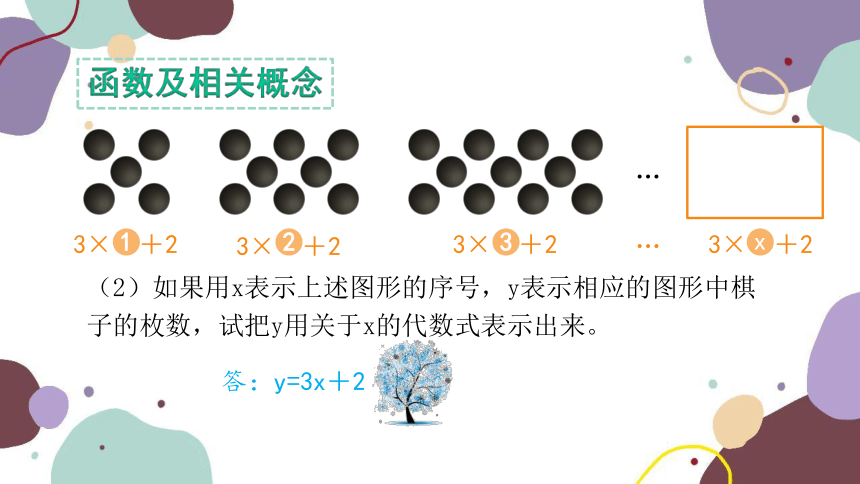
函数及相关概念
(2)如果用x表示上述图形的序号,y表示相应的图形中棋子的枚数,试把y用关于x的代数式表示出来。
答:y=3x+2
x
…
函数及相关概念
(3)在问题(2)中,哪些量是常量?哪些量是变量?y的值是由哪个变量的取值确定的?
答:在问题(2)中,y用关于x的代数式表示为y=3x+2,
例如,当x=4时,y=14(枚)
y的值是由x的取值确定的,
其中3,2是常量,y和x是变量,
你发现y和x之间有什么关系?
函数及相关概念
在同一个变化过程中,有两个变量x和y,如果对于变量x的每一个确定的值,都能随之确定一个y值,我们就把y叫做x的函数,其中x叫做自变量。如果自变量x取a时,y的值是b,就把b叫做x=a时的函数值。
在上面问题中,14是关于x的代数式3x+2当x=4时的值,也叫做函数y=3x+2当x=4时的函数值。
在求函数值时,一定要指明是自变量为多少时的函数值。
函数及相关概念
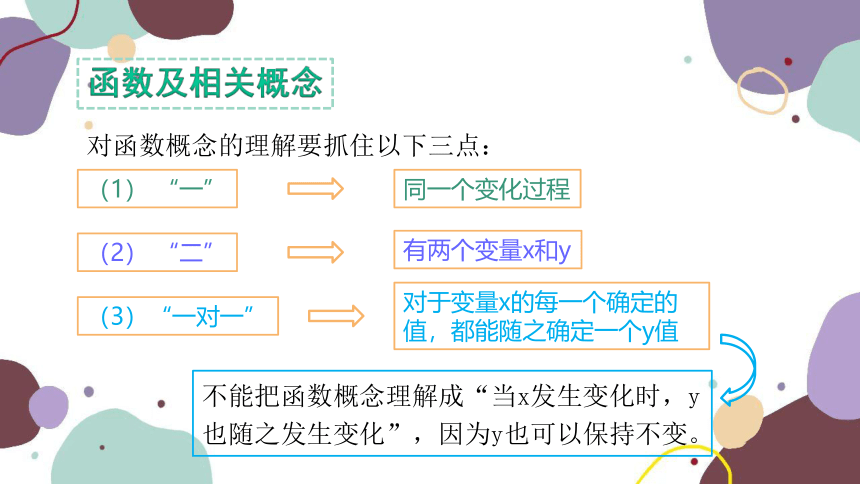
对函数概念的理解要抓住以下三点:
同一个变化过程
有两个变量x和y
对于变量x的每一个确定的值,都能随之确定一个y值
(1) “一”
(2) “二”
(3)“一对一”
不能把函数概念理解成“当x发生变化时,y也随之发生变化”,因为y也可以保持不变。
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的表达式。
表达式
表达式
让我们再进一步了解表达式的概念:
函数表达式是一个等式;
通常等号右边的代数式中的变量是自变量,等号左边的一个变量表示函数;
求y关于x的表达式,必须用含自变量x的代数式表示y.
随堂练习
判断下列问题中两变量之间是不是函数关系:
(1)速度一定时,路程与时间;
答:速度一定时,路程随时间的变化而变化,对于时间所取的每一个确定的值,路程都有唯一确定的值与之对应,所以路程是时间的函数。
随堂练习
(3)小树的高度与小明的体重。
答:小树的高度与小明的体重虽然是两个变量,但这两个变量不是在同一变化过程中,这两个变量没有直接关系,故这两个变量不是函数关系。
考查函数概念问题的解题关键是看在同一个变化过程中,自变量每取一个确定的值时,函数是否有唯一确定的值与之对应。
随堂练习
例1 人行道用同样大小的小正方形水泥地砖铺设而成。
(1)按图①②③…的次序铺设水泥地砖,铺设第④个图形将需要多少块地砖?
①
②
③
…
答:在图中,图①中有3×5块地砖,图②中有5×5块地砖,图③中有5×7块地砖。从第2个图形开始,每个图形都比它前面的一个图形多2列地砖,因此第④个图形应当有5×9=45块地砖。
如图中的每一个小正方形表示一块地砖。
随堂练习
答:根据(1)中发现的规律,第n个图形中地砖的块数应当是5(2n+1),即S=5(2n+1);
(2)如果用n表示上述图形中的序号,S表示第n个图形中地砖的块数,写出S与n之间的表达式。指出在这个问题中哪些量是常量,哪些量是变量,哪个量是哪个量的函数。
(3)铺设序号为100的图形时,需要多少块地砖?
答:当n=100时,S=5×(2×100+1)=1005(块)
在这个问题中,5,2,1是常量,S和n是变量,S是n的函数。
在_______________中,有____________,如果________
__________________________________,我们就把y叫做x的函数,其中x叫做________。如果自变量x取a时,y的值是b,就把b叫做x=a时的_______。
对于变量x的每一个确定的值,都能随之确定一个y值
总结
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的______。
考查函数概念问题的解题关键:
同一个变化过程
两个变量x和y
自变量
函数值
表达式
看在同一个变化过程中,自变量每取一个确定的值时,函数是否有唯一确定的值与之对应。
巩固练习
D
巩固练习
2.根据如图所示的程序,当输入x=6时,输出的
结果y=____
输入x
y=x+4(x≤5)
y=-x+16(x>5)
输出y
10
巩固练习
3.某人公交卡里有50元,每次乘车花费0.8元。如果此人乘车的次数用m表示,每次乘车后的余额用n(元)表示,请写出此人公交卡余额n(元)与乘车的次数m之间的表达式。在这个问题中,n的值由哪几个变量的取值确定的?乘车13次后公交卡内还剩多少元?
解:n=50-0.8m
当m=13时,n=50-0.8×13=39.6(元)
在这个问题中,n的值是由m的取值确定的。
第5章 代数式与函数的初步认识
5.5 函数的初步认识
学习目标
结合实例,了解并能够区分自变量、函数值与函数
对于给定的函数,能根据自变量的值求出函数的值
能根据实际问题列出函数表达式,也能利用函数表达式解决实际问题
3× +2
3× +2
3× +2
函数及相关概念
如图,用棋子按规律摆图形,根据图形的排列规律,解答下列问题:
1
2
3
…
(1)按图中的 的次序这样摆下去,第 个图形中需要多少枚棋子?
1
2
3
4
答:第 个图形中需要3×4+2=14(枚)棋子
4
3× +2
3× +2
3× +2
3× +2
1
2
3
…
函数及相关概念
(2)如果用x表示上述图形的序号,y表示相应的图形中棋子的枚数,试把y用关于x的代数式表示出来。
答:y=3x+2
x
…
函数及相关概念
(3)在问题(2)中,哪些量是常量?哪些量是变量?y的值是由哪个变量的取值确定的?
答:在问题(2)中,y用关于x的代数式表示为y=3x+2,
例如,当x=4时,y=14(枚)
y的值是由x的取值确定的,
其中3,2是常量,y和x是变量,
你发现y和x之间有什么关系?
函数及相关概念
在同一个变化过程中,有两个变量x和y,如果对于变量x的每一个确定的值,都能随之确定一个y值,我们就把y叫做x的函数,其中x叫做自变量。如果自变量x取a时,y的值是b,就把b叫做x=a时的函数值。
在上面问题中,14是关于x的代数式3x+2当x=4时的值,也叫做函数y=3x+2当x=4时的函数值。
在求函数值时,一定要指明是自变量为多少时的函数值。
函数及相关概念
对函数概念的理解要抓住以下三点:
同一个变化过程
有两个变量x和y
对于变量x的每一个确定的值,都能随之确定一个y值
(1) “一”
(2) “二”
(3)“一对一”
不能把函数概念理解成“当x发生变化时,y也随之发生变化”,因为y也可以保持不变。
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的表达式。
表达式
表达式
让我们再进一步了解表达式的概念:
函数表达式是一个等式;
通常等号右边的代数式中的变量是自变量,等号左边的一个变量表示函数;
求y关于x的表达式,必须用含自变量x的代数式表示y.
随堂练习
判断下列问题中两变量之间是不是函数关系:
(1)速度一定时,路程与时间;
答:速度一定时,路程随时间的变化而变化,对于时间所取的每一个确定的值,路程都有唯一确定的值与之对应,所以路程是时间的函数。
随堂练习
(3)小树的高度与小明的体重。
答:小树的高度与小明的体重虽然是两个变量,但这两个变量不是在同一变化过程中,这两个变量没有直接关系,故这两个变量不是函数关系。
考查函数概念问题的解题关键是看在同一个变化过程中,自变量每取一个确定的值时,函数是否有唯一确定的值与之对应。
随堂练习
例1 人行道用同样大小的小正方形水泥地砖铺设而成。
(1)按图①②③…的次序铺设水泥地砖,铺设第④个图形将需要多少块地砖?
①
②
③
…
答:在图中,图①中有3×5块地砖,图②中有5×5块地砖,图③中有5×7块地砖。从第2个图形开始,每个图形都比它前面的一个图形多2列地砖,因此第④个图形应当有5×9=45块地砖。
如图中的每一个小正方形表示一块地砖。
随堂练习
答:根据(1)中发现的规律,第n个图形中地砖的块数应当是5(2n+1),即S=5(2n+1);
(2)如果用n表示上述图形中的序号,S表示第n个图形中地砖的块数,写出S与n之间的表达式。指出在这个问题中哪些量是常量,哪些量是变量,哪个量是哪个量的函数。
(3)铺设序号为100的图形时,需要多少块地砖?
答:当n=100时,S=5×(2×100+1)=1005(块)
在这个问题中,5,2,1是常量,S和n是变量,S是n的函数。
在_______________中,有____________,如果________
__________________________________,我们就把y叫做x的函数,其中x叫做________。如果自变量x取a时,y的值是b,就把b叫做x=a时的_______。
对于变量x的每一个确定的值,都能随之确定一个y值
总结
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的______。
考查函数概念问题的解题关键:
同一个变化过程
两个变量x和y
自变量
函数值
表达式
看在同一个变化过程中,自变量每取一个确定的值时,函数是否有唯一确定的值与之对应。
巩固练习
D
巩固练习
2.根据如图所示的程序,当输入x=6时,输出的
结果y=____
输入x
y=x+4(x≤5)
y=-x+16(x>5)
输出y
10
巩固练习
3.某人公交卡里有50元,每次乘车花费0.8元。如果此人乘车的次数用m表示,每次乘车后的余额用n(元)表示,请写出此人公交卡余额n(元)与乘车的次数m之间的表达式。在这个问题中,n的值由哪几个变量的取值确定的?乘车13次后公交卡内还剩多少元?
解:n=50-0.8m
当m=13时,n=50-0.8×13=39.6(元)
在这个问题中,n的值是由m的取值确定的。
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
