勾股定理的应用 导学案

勾股定理的应用 导学案
学习目标：
我们应该能进一步熟练地运用勾股定理，并利用勾股定理在数轴上确定一些无理数的对应点（重点）
我们应该会利用勾股定理计算立体图形的线段长（重点）
我们应该会将立体图形转化为平面图形，并会利用方程和勾股定理熟练进行有关计算（难点）
学习过程：
一、全员上板展写
展写内容为：用语言（符号）表述勾股定理的内容及常用的勾股定理的变式。
（对子之间互评）
二、重申目标（学法指导：学生齐读学习目标，明确本节课学习的重难点）
三、预习交流：（学法指导：先组内交流，再由B号学生抢答，并简单说明理由）
认真研读教材25~27页，完成下列各题：
1、例2中当梯子在地面上滑动时，梯子AB的长度 变化，此问题可转化为已知
和 ，求 ，故，可以用勾股定理来解答。
2、利用勾股定理可以发现长为的线段是直角边为整数 和 的直角三角形的斜边，故可在数轴上找到点A，使OA= ,过点A作直线l垂直于OA，在直线l上截取AB= ，以原点O为圆心，以OB为半径画弧与数轴交点C，即为表示 的点。
3、如图所示，点A表示的数是（ ）
A 1 B C 1.5 D
4、一个圆柱形的饭盒，底面半径是8cm,高为12cm，若往里放一双筷子（粗细忽略不计），那么筷子最长不超过 可以正好盖上盒盖。
四、问题解决
题型一 勾股定理与方程（组）的综合应用
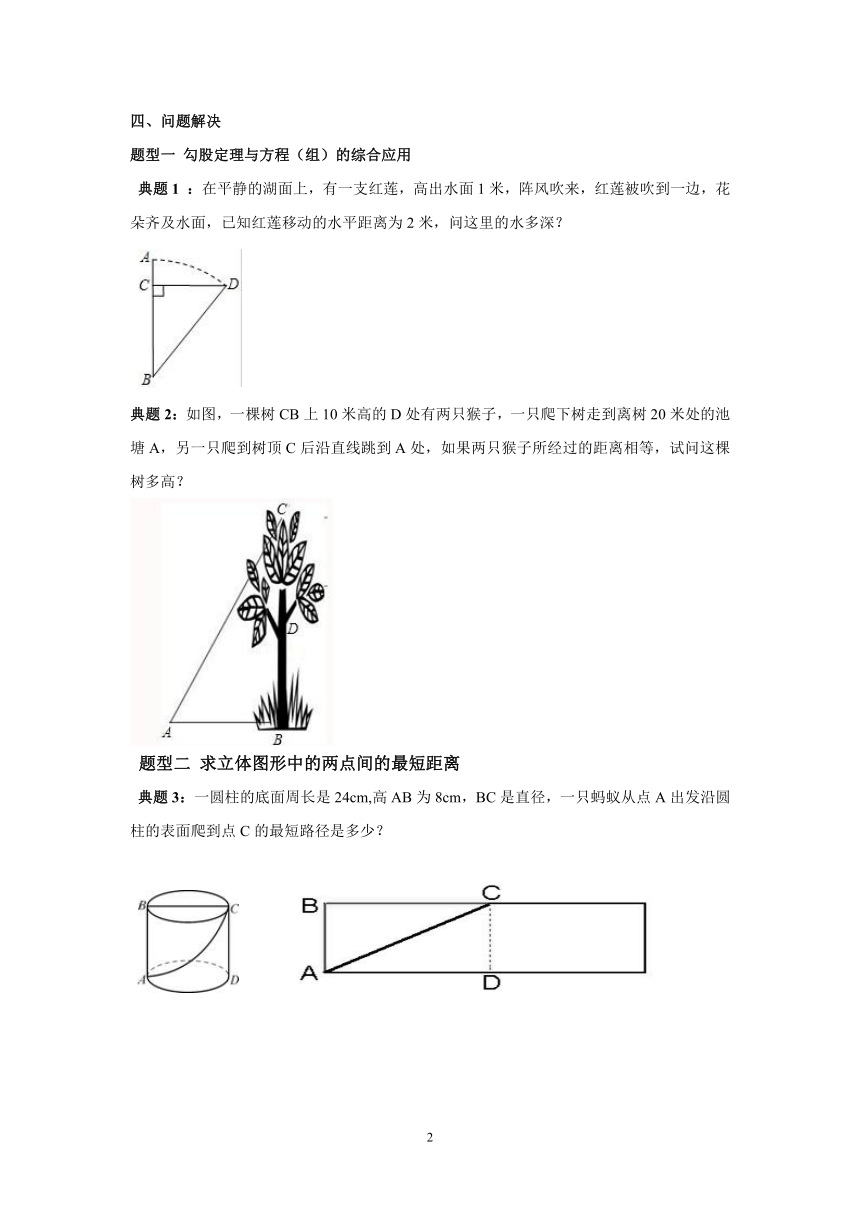
典题1 ：在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，问这里的水多深？
典题2：如图，一棵树CB上10米高的D处有两只猴子，一只爬下树走到离树20米处的池塘A，另一只爬到树顶C后沿直线跳到A处，如果两只猴子所经过的距离相等，试问这棵树多高？
题型二 求立体图形中的两点间的最短距离
典题3：一圆柱的底面周长是24cm,高AB为8cm，BC是直径，一只蚂蚁从点A出发沿圆柱的表面爬到点C的最短路径是多少？
典题4:如图，一只昆虫从棱长为2的正方体的顶点A爬到顶点B，需爬的最短路径有多远？
题型三 勾股定理在折叠问题中的应用
典题5 ：如图，在矩形纸片ABCD中，AB=6，BC=8，现将其沿EF进行对折，使点C与点A重合，则AF的长是多少？
（学法指导：先组内合作探讨，抽签决定所讲题目，每两组讲解同一典题，较好的组有额外奖励5分，其他同学纠错、评价，教师巡视指导）
五、方法指导
1、应用勾股定理构造方程时，要分清各边存在的和、差、倍、分等关系；
2、求立体图形上两点间的距离时，应把它转化为平面图形进行求解（转化思想）；
3、折叠问题时要注意折叠后的图形与原图形全等（中考的考点之一）。
4、教师根据学生在课堂上的展写展讲情况，分别从易错点、易漏点，提升点上准确性深入性做出精而准的点拨。
六、课堂小结、作业
1、组内交流收获并与大家分享，组内探讨没有解决的问题，并提出，寻求大家的帮忙。
2、作业：练习册
七、当堂检测
1、如图所示，数轴上的点A表示的数x，则x的值为（ ）
A B ﹣ C 2 D ﹣2
2、如图，台风后，某校的旗杆在离地某处断裂，旗杆顶部离旗杆底部8米处，已知旗杆的原长为16米，则旗杆在离地 米处断裂。
3、已知：如图，△ABC中，AB=3，BC=4，∠B=90°，若将△ABC折叠，使C点与A点重合，则折痕EF的长为 。
（ 3题图 ） （ 2题图 ） （ 能力拓展题图 ）
4、如图，圆柱的高为10 cm，底面半径为2 cm.，在下底面的A点处有一只蚂蚁，它想吃到上底面上与A点相对的B点处，需要爬行的最短路程是
学法指导：学生独立完成(限时5分钟)，抽签公布答案，对子互判，均分作为本组加分。
能力拓展：（选做题）
如图，长方体的高为3 cm，底面是边长为2 cm的正方形. 现有一小虫从顶点A出发，沿长方体侧面到达顶点C处，小虫走的路程最短为 。
八、布置预习
完成《勾股定理的应用（2）》的预习交流部分
PAGE
4