多边形的内角和与外角和[下学期]
文档属性
| 名称 | 多边形的内角和与外角和[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 47.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-24 08:00:00 | ||
图片预览


文档简介
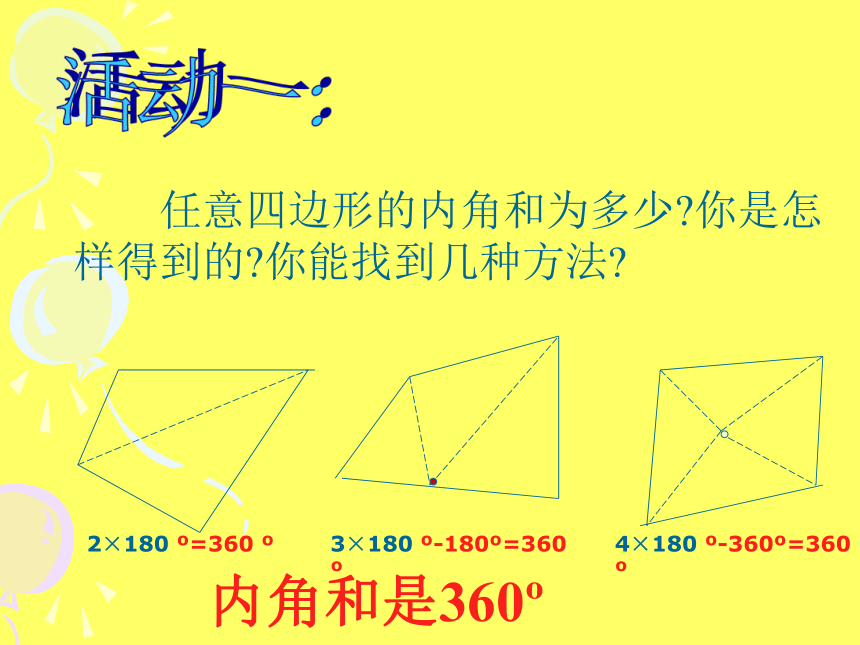
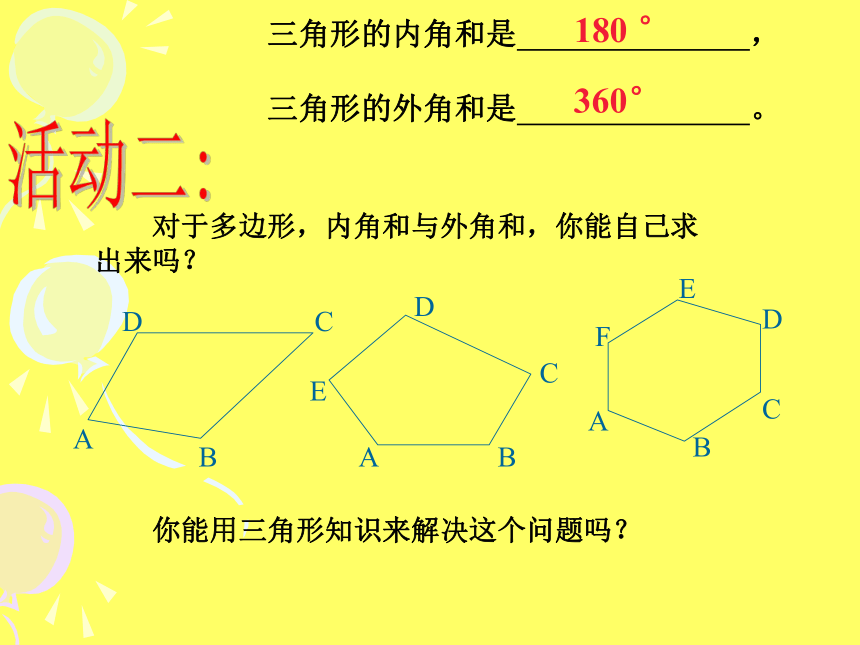
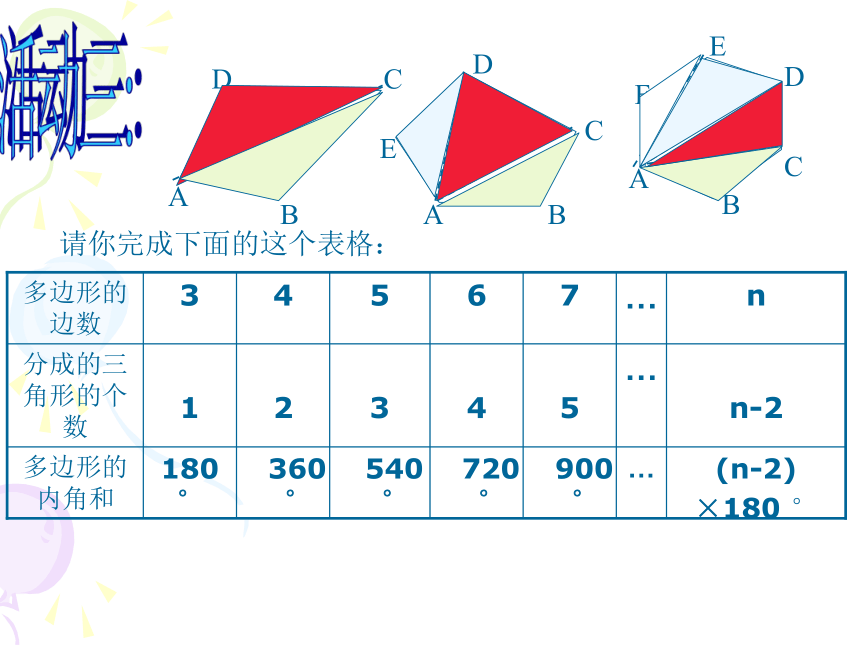
课件14张PPT。多边形的内角和回顾:1,三角形的内角和是多少?2,以前我们学习过哪些四边形的内角和?活动一: 任意四边形的内角和为多少?你是怎样得到的?你能找到几种方法?内角和是360o2×180 o=360 o3×180 o-180o=360 o4×180 o-360o=360 o三角形的内角和是 , 三角形的外角和是 。 对于多边形,内角和与外角和,你能自己求出来吗?你能用三角形知识来解决这个问题吗?180 °360°活动二:请你完成下面的这个表格:(n-2)
×180 °900 °720 °540 °360 °
n-2
5
4
3
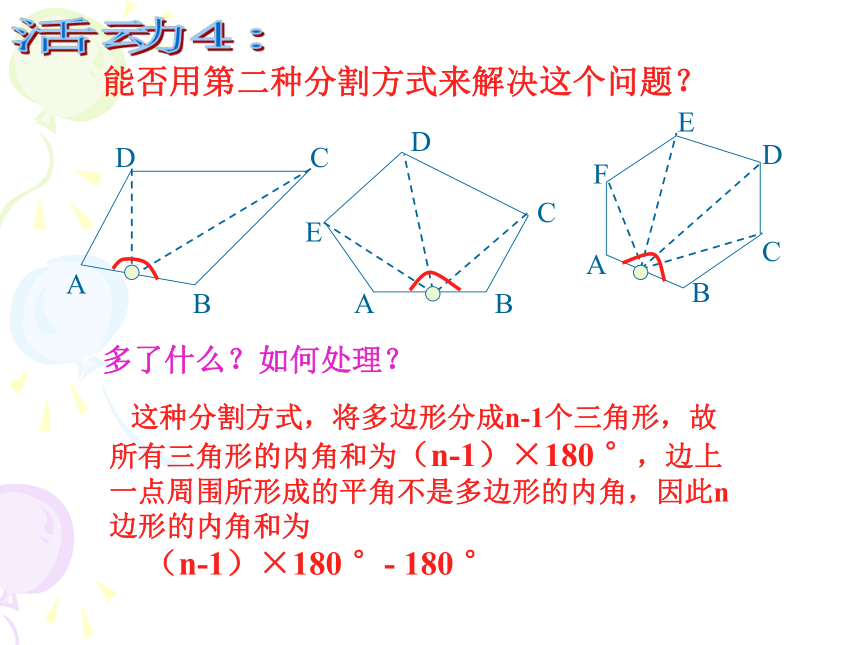
2活动三:能否用第二种分割方式来解决这个问题?多了什么?如何处理? 这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °活动4: 该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °能否用第三种分割方式来解决这个问题?多了什么?如何处理?活动5:多边形的内角和定理:任意n边形的内角和都是(n-2)×180 °多边形的外角和 指出右边多边形的内角与外角。 多边形的外角与它相邻的内角的关系 。 请你动手来实践一下,看看谁能最先找出来四边形的外角和?互 补活动6:任意多边形的外角和为 。360 °360 °360 °360 °(n-2)×180°720 °540 °360 °n×180°6×180° =1080 °5×180°
=900 °4×180° =720 °…360°外角和…180°内角和…3×180°
=540 °内外角总和n…543边数请你完成下面的这个表格:360 °能力训练:1、十边形的内角和是 ,外角和是 。2、正八边形的内角和是 ,每个内角的度数是 。3、一多边形的每个内角都等于120°,则其每一个外角是 ,它是 边形。4、一多边形的内角和1260 ° ,则其边数 。5、一个多边形的每个外角都是30 ° ,则此多边形的内角和是 。6、五边形的内角和与外角和的比值是 。1440 °360 °1080 °135 °60 °六九1800 °3:2思考题:ACBO12 你获得了哪些新知识:1、多边形的内角和为:2、多边形的外角和为:作业:P56 习题2、3、4题
×180 °900 °720 °540 °360 °
n-2
5
4
3
2活动三:能否用第二种分割方式来解决这个问题?多了什么?如何处理? 这种分割方式,将多边形分成n-1个三角形,故所有三角形的内角和为(n-1)×180 °,边上一点周围所形成的平角不是多边形的内角,因此n边形的内角和为 (n-1)×180 °- 180 °活动4: 该图中n边形共有n个三角形,故所有三角形内角和为n×180 °,但每个图中都有一个以红圈圈住的点,它是一个圆周角360 °,因此n边形的内角和为 n×180 °- 360 °能否用第三种分割方式来解决这个问题?多了什么?如何处理?活动5:多边形的内角和定理:任意n边形的内角和都是(n-2)×180 °多边形的外角和 指出右边多边形的内角与外角。 多边形的外角与它相邻的内角的关系 。 请你动手来实践一下,看看谁能最先找出来四边形的外角和?互 补活动6:任意多边形的外角和为 。360 °360 °360 °360 °(n-2)×180°720 °540 °360 °n×180°6×180° =1080 °5×180°
=900 °4×180° =720 °…360°外角和…180°内角和…3×180°
=540 °内外角总和n…543边数请你完成下面的这个表格:360 °能力训练:1、十边形的内角和是 ,外角和是 。2、正八边形的内角和是 ,每个内角的度数是 。3、一多边形的每个内角都等于120°,则其每一个外角是 ,它是 边形。4、一多边形的内角和1260 ° ,则其边数 。5、一个多边形的每个外角都是30 ° ,则此多边形的内角和是 。6、五边形的内角和与外角和的比值是 。1440 °360 °1080 °135 °60 °六九1800 °3:2思考题:ACBO12 你获得了哪些新知识:1、多边形的内角和为:2、多边形的外角和为:作业:P56 习题2、3、4题
