6.3.1等可能事件的概率(第1课时) 课件(16张PPT)
文档属性
| 名称 | 6.3.1等可能事件的概率(第1课时) 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 461.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 10:53:04 | ||
图片预览






文档简介
(共16张PPT)
北师大版七年级数学下册
第六章 概率初步
3.1 等可能事件的概率
崇德尚礼 笃学求真
学习&目标
1.通过摸球游戏,帮助学生了解计算等可能事件的概率的方法,体会概率的意义;(重点)
2.灵活应用概率的计算方法解决各种类型的实际问题.(难点)
情境&导入
前面我们用事件发生的频率来估计该事件发生的概率,但得到的往往只是概率的估计值. 那么,还有没有其他求概率的方法呢
探索&交流
试验1 抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:各点数出现的可能性大小是多少?
6种
相等
探索&交流
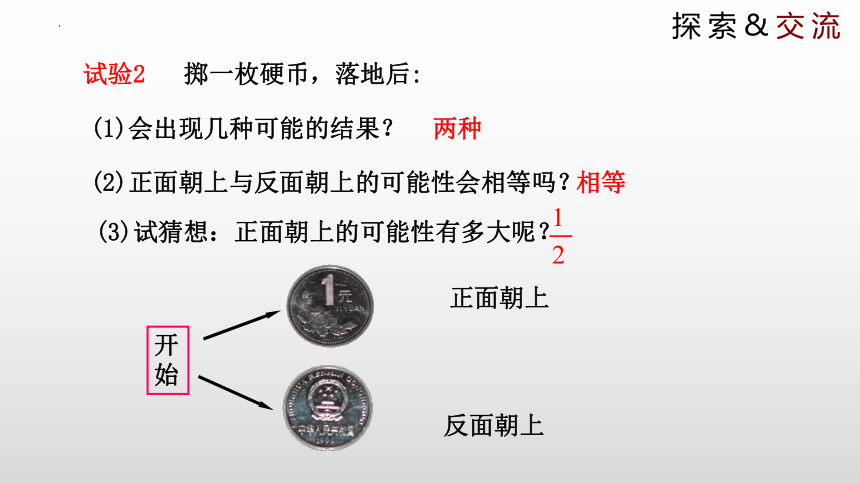
试验2 掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
相等
探索&交流
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等.
具有两个共同特征:
上述试验都具有什么样的共同特点?
具有上述特点的试验,我们可以用事件所包含的各种可能的结果数在全部可能的结果数中所占的比,来表示事件发生的概率.
在这些试验中出现的事件为等可能事件.
探索&交流
议一议
一个袋中有5个球,分别标有1,2,3,4,5这5个号码,这些球除号码外都相同,搅匀后任意摸出一个球。
(1)会出现哪些可能的结果?
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
(1)会出现标有 1,2,3,4,5 小球的五种情况.
(2)每个结果出现的可能性相同.它们的概率分别是 .
探索&交流
2.前面我们提到的抛硬币、 掷骰子和摸球的游戏有什么共同的特点?
(1)所有可能出现的不同结果是有限个;
(2)各种不同结果出现的可能性相等.
探索&交流
设一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
探索&交流
你能找一些结果是等可能的试验吗?
一般地, 如果一个试验有 n 种等可能的结果, 事件 A 包含其中的 m 种结果, 那么事件 A 发生的概率为: .
做一做
例题&解析
例题欣赏
例1.任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚均匀骰子,所有可能的结果有6种:掷出的点数分别是1,2,3,4,5,6,因为骰子是均匀的,所以每种结果出现的可能性相等。
例题&解析
(1) 掷出的点数大于4的结果只有 2 种:掷出的点数分别是 5,6,所以 P(掷出的点数大于4)
(2)掷出的点数是偶数的结果有 3 种: 掷出的点数分别是 2,4,6,所以P(掷出的点数是偶数)
练习&巩固
1.下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
练习&巩固
2.在一个不透明的口袋中装有5个完全相同的小球,它们分别标有1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
A. B.
C. D.
练习&巩固
3.一个桶里有60个弹珠——一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是35%,拿出蓝色弹珠的概率是25%.桶里每种颜色的弹珠各有多少?
小结&反思
1.频率的稳定性.
2.事件A的概率,记为P(A).
3.一般的,大量重复的实验中,我们常用不确定事件 A 发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件 A 发生的概率P(A)是0与1之间的一个常数.
北师大版七年级数学下册
第六章 概率初步
3.1 等可能事件的概率
崇德尚礼 笃学求真
学习&目标
1.通过摸球游戏,帮助学生了解计算等可能事件的概率的方法,体会概率的意义;(重点)
2.灵活应用概率的计算方法解决各种类型的实际问题.(难点)
情境&导入
前面我们用事件发生的频率来估计该事件发生的概率,但得到的往往只是概率的估计值. 那么,还有没有其他求概率的方法呢
探索&交流
试验1 抛掷一个质地均匀的骰子
(1)它落地时向上的点数有几种可能的结果?
(2)各点数出现的可能性会相等吗?
(3)试猜想:各点数出现的可能性大小是多少?
6种
相等
探索&交流
试验2 掷一枚硬币,落地后:
(1)会出现几种可能的结果?
(2)正面朝上与反面朝上的可能性会相等吗?
(3)试猜想:正面朝上的可能性有多大呢?
开始
正面朝上
反面朝上
两种
相等
探索&交流
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等.
具有两个共同特征:
上述试验都具有什么样的共同特点?
具有上述特点的试验,我们可以用事件所包含的各种可能的结果数在全部可能的结果数中所占的比,来表示事件发生的概率.
在这些试验中出现的事件为等可能事件.
探索&交流
议一议
一个袋中有5个球,分别标有1,2,3,4,5这5个号码,这些球除号码外都相同,搅匀后任意摸出一个球。
(1)会出现哪些可能的结果?
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
(1)会出现标有 1,2,3,4,5 小球的五种情况.
(2)每个结果出现的可能性相同.它们的概率分别是 .
探索&交流
2.前面我们提到的抛硬币、 掷骰子和摸球的游戏有什么共同的特点?
(1)所有可能出现的不同结果是有限个;
(2)各种不同结果出现的可能性相等.
探索&交流
设一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
探索&交流
你能找一些结果是等可能的试验吗?
一般地, 如果一个试验有 n 种等可能的结果, 事件 A 包含其中的 m 种结果, 那么事件 A 发生的概率为: .
做一做
例题&解析
例题欣赏
例1.任意掷一枚均匀骰子。
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚均匀骰子,所有可能的结果有6种:掷出的点数分别是1,2,3,4,5,6,因为骰子是均匀的,所以每种结果出现的可能性相等。
例题&解析
(1) 掷出的点数大于4的结果只有 2 种:掷出的点数分别是 5,6,所以 P(掷出的点数大于4)
(2)掷出的点数是偶数的结果有 3 种: 掷出的点数分别是 2,4,6,所以P(掷出的点数是偶数)
练习&巩固
1.下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
练习&巩固
2.在一个不透明的口袋中装有5个完全相同的小球,它们分别标有1,2,3,4,5,从中随机摸出一个小球,其标号是奇数的概率为( )
A. B.
C. D.
练习&巩固
3.一个桶里有60个弹珠——一些是红色的,一些是蓝色的,一些是白色的.拿出红色弹珠的概率是35%,拿出蓝色弹珠的概率是25%.桶里每种颜色的弹珠各有多少?
小结&反思
1.频率的稳定性.
2.事件A的概率,记为P(A).
3.一般的,大量重复的实验中,我们常用不确定事件 A 发生的频率来估计事件A发生的概率.
4.必然事件发生的概率为1;
不可能事件发生的概率为0;
随机事件 A 发生的概率P(A)是0与1之间的一个常数.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
