1.2 配方法 课件（22张PPT）

(共22张PPT)
1.2 一元二次方程
——配方法 （二次项系数不为1）
第一章 一元二次方程
目 录
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
6 随堂检测
学习目标
1.理解配方的基本过程，会运用配方法解二次项系数
不为1的一元二次方程. （重点）
2.经历探索利用配方法解一元二次方程的过程，
体会转化的数学思想.
新课导入
新课导入
比较方程x2－ x+1=0与方程2x2－5x+2=0有什么关系？
后一个方程中的二次项系数变为1，即方程两边都除以2就得到前一个方程 ，这样就转化为学过的方程的形式，用配方法即可求出方程的解
新课讲解
解：
常数项移到“＝”右边
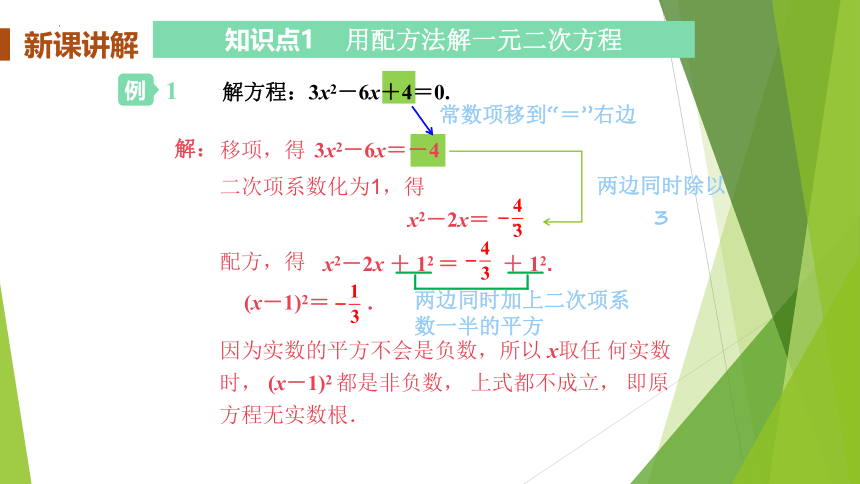
1 解方程：3x2－6x＋4＝0.
移项，得 3x2－6x＝－4
二次项系数化为1，得
配方，得
因为实数的平方不会是负数，所以 x取任 何实数时， (x－1)2 都是非负数， 上式都不成立， 即原方程无实数根．　　　　
x2－2x＝ .
x2－2x ＋ 12 ＝ ＋ 12.
(x－1)2＝ .
两边同时除以3
两边同时加上二次项系数一半的平方
例
知识点1 用配方法解一元二次方程
　 移项，得 2x2－3x＝－1.
二次项系数化为1，得
配方，得
由此可得　　　　　　　　　　
1.解方程2x2＋1＝3x.
练一练
2.解方程
和前面解的方程有什么不同？
分析：
如果二次项的系数能化为1，那么就可以用配方法求解。你能把它变为1吗？如何变？
解
移项，得
两边同除以4，得
配方，得
即
你能总结出配方法
解方程的步骤吗？
练一练
2.当x取何值时，代数式2x2－6x＋7的值最小？
并求出这个最小值．
分析：求代数式的最小值，先将代数式配方成
a(x＋m)2 ＋n的形式，然后根据完全平
方的非负性求代数式的最小值．
知识点2 二次三项式的配方
例
解： 2x2－6x＋7
1、通过配方，把方程的左边化为完全平方式，然后用直接开平方法解方程的方法叫做配方法。
2、用配方法解一元二次方程的步骤：
(1)把方程中含有未知数的项移到左边，
常数项移到右边；
(2)把二次项系数化为1；
(3)方程两边同时加上一次项系数一半的平方；
(4)将方程变为(x+m)2=n的形式；
(5)当n≥0时，用直接开平方法解变形后的方程。
课堂小结
课堂小结
用配方法解一元二次方程的步骤:
一般步骤 方法
一移 移项 将常数项移到右边，含未知数的项移到左边
二化 二次项系数化为1 左、右两边同时除以二次项系数
三配 配方 左、右两边同时加上一次项系数一半的平方
四开 开平方 利用平方根的意义直接开平方
五解 解两个一元一次方程 移项，合并
当堂小练
1.下列用配方法解方程2x2－x－6＝0，开始出现错误的步骤是(　　)
2x2－x＝6， ①
， ②
， ③
④
A．①　　 B．②　 C．③　　 D．④
C
2.解方程2x2－5x＋2＝0.
解：两边都除以2，得
移项，得
配方，得
两边开平方，得
∴ ， ．
3.解方程－3x2＋4x＋1＝0．
解：两边都除以－3，得
移项，得
配方，得
两边开平方，得
∴　　　　　　　　　　　　．
4.当a为何值时，多项式a2+2a+18有最小值？并求出
这个最小值.
解：对原式进行配方，则原式=(a+1)2+17
∵(a+1)2≥0,
∴当a=-1时，原式有最小值为17.
随堂检测
C