物理人教版(2019)必修二册 8.3 动能和动能定理(共20张ppt)
文档属性
| 名称 | 物理人教版(2019)必修二册 8.3 动能和动能定理(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-03 07:45:18 | ||
图片预览







文档简介
(共20张PPT)
第八章 机械能守恒定律
第三节 动能和动能定理
思考:物体的动能与哪些因素有关?
动能与物体的质量m和运动的速度v有关,且质量越大,速度越大,动能越大。
物体由于运动而具有的能叫动能。
动 能
1、概念:物体由于运动具有的能量叫做动能。
2、定义式:
1
2
Ek= mv2
3、性质:
动能是描述物体运动状态的物理量。
动能是标量,只有大小,没有方向,计算为正值。
动能是状态量,具有瞬时性,相对性。
单位:焦耳(J)【1J=1kg·m2/s2】
练习:思考判断
(1)动能是机械能的一种,凡是运动的物体都具有动能 ( )
(2)动能总是非负值 ( )
(3)两个物体中,速度大的动能也大。 ( )
(4)某物体的速度加倍,它的动能也加倍。( )
(5)做匀速圆周运动的物体动能保持不变 ( )
试比较下列每种情况下,甲、乙两物体的动能:
(除题意中提到的物理量外,其他物理情况相同)
总结:动能是标量,与速度方向无关;
动能与速度的平方成正比,因此速度对动能的影响更大。
①物体甲做直线运动,乙做曲线运动;
②物体甲向北运动,乙向南运动;
③物体甲的速度是乙的两倍;
④物体甲的质量是乙的一半。
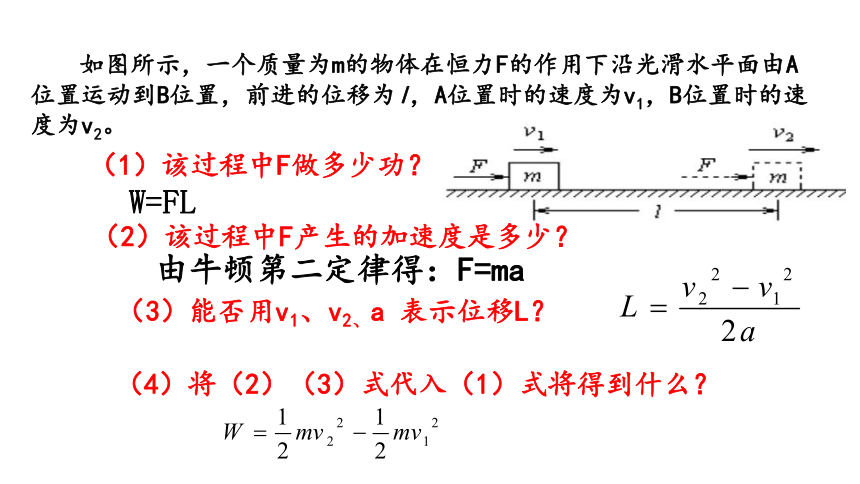
(2)该过程中F产生的加速度是多少?
(3)能否用v1、v2、a 表示位移L?
(4)将(2)(3)式代入(1)式将得到什么?
如图所示,一个质量为m的物体在恒力F的作用下沿光滑水平面由A位置运动到B位置,前进的位移为l,A位置时的速度为v1,B位置时的速度为v2。
(1)该过程中F做多少功?
W=FL
由牛顿第二定律得:F=ma
粗糙水平面上,质量为m的物体,在与运动方向相同的恒力F 的作用下发生一段位移l,速度由v1增加到v2,已知阻力恒定为f,试求这个过程中合外力做的功。
根据牛顿第二定律有: F-f=ma
速度与位移的关系式:
得:
= ma×
整理得:
W合=( F-f )l
外力的总功
末状态动能
初状态动能
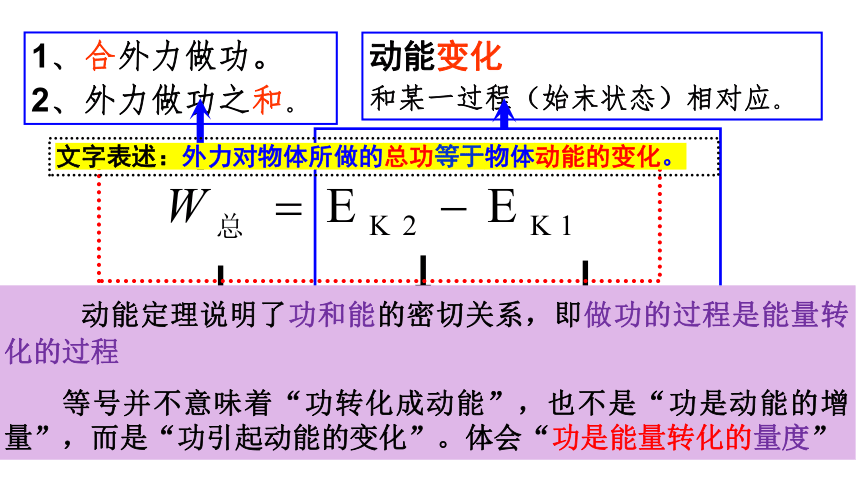
1、合外力做功。
2、外力做功之和。
动能变化
和某一过程(始末状态)相对应。
动能定理说明了功和能的密切关系,即做功的过程是能量转化的过程
等号并不意味着“功转化成动能”,也不是“功是动能的增量”,而是“功引起动能的变化”。体会“功是能量转化的量度”
文字表述:外力对物体所做的总功等于物体动能的变化。
对动能定理的理解
a、力对“物体”做功与“物体”动能变化中“物体”要相同,即同一物体.
三个相同
b、由于动能定理式子中的x、v跟参考系的选取有关,应取同一参考系---地球.
c、物体做功的“过程”应与物体动能变化的“过程”一样,即同一过程.
如图所示,AB为固定在竖直平面内的 光滑圆弧轨道,轨道的B点与水平地面相切,其半径为R。质量为m的小球由A点静止释放,求:
(1)小球滑到最低点B时,小球速度v的大小;
(2)小球刚到达最低点B时,轨道对小球支持力FN的大小;
(3)小球通过光滑的水平面BC滑上固定曲面,恰达最高点D,D到地面的高度为H(己知h二、动能定理
动力学问题两种解法的比较:
比较 项 牛顿运动定律和运动学公式结合 动能定理
适用 条件 只能研究在恒力作用下物体做直线运动的情况 对于物体在恒力或变力作用下,物体做直线运动或曲线运动均适用
应用 方法 要考虑运动过程的每一个细节 只考虑各力的做功情况及初、末状态的动能,不关注细节
运算 方法 矢量运算 代数运算
人们有时用“打夯”的方式把松散的地面夯实。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
【解析】(1)两根绳子对重物的合力
F合= 2 F cos 37°=2×320×0.8 N=512 N
由A至E的过程中,应用动能定理可得
(2)由E到F的过程中,应用动能定理可得
重物落地时的速度大小为2.5 m/s,对地面的平均冲击力的大小为8.3×103N
H
B
A
mg
T合
mg
C
D
E
F
【例1】如图为高速摄影机
拍摄到的子弹穿过苹果瞬间的照
片。子弹击中苹果前的瞬间速度
约为900m/s,穿出苹果瞬间的速
度约为为800m/s,子弹的质量约为20g ,在苹果中穿行的路径约为10cm。试估算子弹穿过苹果的过程中对苹果的平均冲力?
拓展应用
解:对子弹由动能定理有
1、选对象
v
2确定各力做功
4列方程
2受力分析
动能定理
G
FN
由牛顿第三定律,苹果受的平均冲力为
3分析运动,定初末
f
总结:动能定理解题步骤
1、定对象,选过程;
2、析受力,算总功;
3、知运动,定初末;
4、列方程,细求解。
第八章 机械能守恒定律
第三节 动能和动能定理
思考:物体的动能与哪些因素有关?
动能与物体的质量m和运动的速度v有关,且质量越大,速度越大,动能越大。
物体由于运动而具有的能叫动能。
动 能
1、概念:物体由于运动具有的能量叫做动能。
2、定义式:
1
2
Ek= mv2
3、性质:
动能是描述物体运动状态的物理量。
动能是标量,只有大小,没有方向,计算为正值。
动能是状态量,具有瞬时性,相对性。
单位:焦耳(J)【1J=1kg·m2/s2】
练习:思考判断
(1)动能是机械能的一种,凡是运动的物体都具有动能 ( )
(2)动能总是非负值 ( )
(3)两个物体中,速度大的动能也大。 ( )
(4)某物体的速度加倍,它的动能也加倍。( )
(5)做匀速圆周运动的物体动能保持不变 ( )
试比较下列每种情况下,甲、乙两物体的动能:
(除题意中提到的物理量外,其他物理情况相同)
总结:动能是标量,与速度方向无关;
动能与速度的平方成正比,因此速度对动能的影响更大。
①物体甲做直线运动,乙做曲线运动;
②物体甲向北运动,乙向南运动;
③物体甲的速度是乙的两倍;
④物体甲的质量是乙的一半。
(2)该过程中F产生的加速度是多少?
(3)能否用v1、v2、a 表示位移L?
(4)将(2)(3)式代入(1)式将得到什么?
如图所示,一个质量为m的物体在恒力F的作用下沿光滑水平面由A位置运动到B位置,前进的位移为l,A位置时的速度为v1,B位置时的速度为v2。
(1)该过程中F做多少功?
W=FL
由牛顿第二定律得:F=ma
粗糙水平面上,质量为m的物体,在与运动方向相同的恒力F 的作用下发生一段位移l,速度由v1增加到v2,已知阻力恒定为f,试求这个过程中合外力做的功。
根据牛顿第二定律有: F-f=ma
速度与位移的关系式:
得:
= ma×
整理得:
W合=( F-f )l
外力的总功
末状态动能
初状态动能
1、合外力做功。
2、外力做功之和。
动能变化
和某一过程(始末状态)相对应。
动能定理说明了功和能的密切关系,即做功的过程是能量转化的过程
等号并不意味着“功转化成动能”,也不是“功是动能的增量”,而是“功引起动能的变化”。体会“功是能量转化的量度”
文字表述:外力对物体所做的总功等于物体动能的变化。
对动能定理的理解
a、力对“物体”做功与“物体”动能变化中“物体”要相同,即同一物体.
三个相同
b、由于动能定理式子中的x、v跟参考系的选取有关,应取同一参考系---地球.
c、物体做功的“过程”应与物体动能变化的“过程”一样,即同一过程.
如图所示,AB为固定在竖直平面内的 光滑圆弧轨道,轨道的B点与水平地面相切,其半径为R。质量为m的小球由A点静止释放,求:
(1)小球滑到最低点B时,小球速度v的大小;
(2)小球刚到达最低点B时,轨道对小球支持力FN的大小;
(3)小球通过光滑的水平面BC滑上固定曲面,恰达最高点D,D到地面的高度为H(己知h
动力学问题两种解法的比较:
比较 项 牛顿运动定律和运动学公式结合 动能定理
适用 条件 只能研究在恒力作用下物体做直线运动的情况 对于物体在恒力或变力作用下,物体做直线运动或曲线运动均适用
应用 方法 要考虑运动过程的每一个细节 只考虑各力的做功情况及初、末状态的动能,不关注细节
运算 方法 矢量运算 代数运算
人们有时用“打夯”的方式把松散的地面夯实。设某次打夯符合以下模型:两人同时通过绳子对重物各施加一个力,力的大小均为320 N,方向都与竖直方向成37°,重物离开地面30 cm后人停止施力,最后重物自由下落把地面砸深2 cm。已知重物的质量为50 kg, g取10 m/s2, cos 37°=0.8。求:
(1)重物刚落地时的速度是多大?
(2)重物对地面的平均冲击力是多大?
【解析】(1)两根绳子对重物的合力
F合= 2 F cos 37°=2×320×0.8 N=512 N
由A至E的过程中,应用动能定理可得
(2)由E到F的过程中,应用动能定理可得
重物落地时的速度大小为2.5 m/s,对地面的平均冲击力的大小为8.3×103N
H
B
A
mg
T合
mg
C
D
E
F
【例1】如图为高速摄影机
拍摄到的子弹穿过苹果瞬间的照
片。子弹击中苹果前的瞬间速度
约为900m/s,穿出苹果瞬间的速
度约为为800m/s,子弹的质量约为20g ,在苹果中穿行的路径约为10cm。试估算子弹穿过苹果的过程中对苹果的平均冲力?
拓展应用
解:对子弹由动能定理有
1、选对象
v
2确定各力做功
4列方程
2受力分析
动能定理
G
FN
由牛顿第三定律,苹果受的平均冲力为
3分析运动,定初末
f
总结:动能定理解题步骤
1、定对象,选过程;
2、析受力,算总功;
3、知运动,定初末;
4、列方程,细求解。
