沪科版八年级数学下册18.2勾股定理的逆定理 试题 (含答案)
文档属性
| 名称 | 沪科版八年级数学下册18.2勾股定理的逆定理 试题 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 00:00:00 | ||
图片预览


文档简介
18.2勾股定理的逆定理
一、选择题
1.以下列各组数为边长能组成直角三角形的是( )
A.2、3、4 B.、、 C.32、42、52 D.6、8、10
2.下列几组数中,不能作为直角三角形的三边长的是( )
A.4,9,11 B.6,8,10 C.7,24,25 D.8,15,17
3.下列不能判定△ABC是直角三角形的是( )
A.a2+b2﹣c2=0 B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5 D.∠A+∠B=∠C
4.若△ABC中,AB=c,AC=b,BC=a,下列不能判定△ABC为直角三角形的是( )
A.a=32,b=42,c=52 B.a:b:c=5:12:13
C.(c+b)(c﹣b)=a2 D.∠A+∠B=∠C
5.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
6.如图,一棵大树在离地面3m,5m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部6m处,则大树折断前的高度是( )
A.9m B.14m C.11m D.10m
7.在△ABC中,若AC2﹣BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
8.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2﹣c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
10.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.2 B.2 C.4 D.4
二.填空题
11.如图中的每个小方格都是边长为1的正方形,那么∠ABC的度数是 .
12.在△ABC中,如果AB=m2﹣n2,AC=2mn,BC=m2+n2,则△ABC是 三角形,其中∠ =90°.
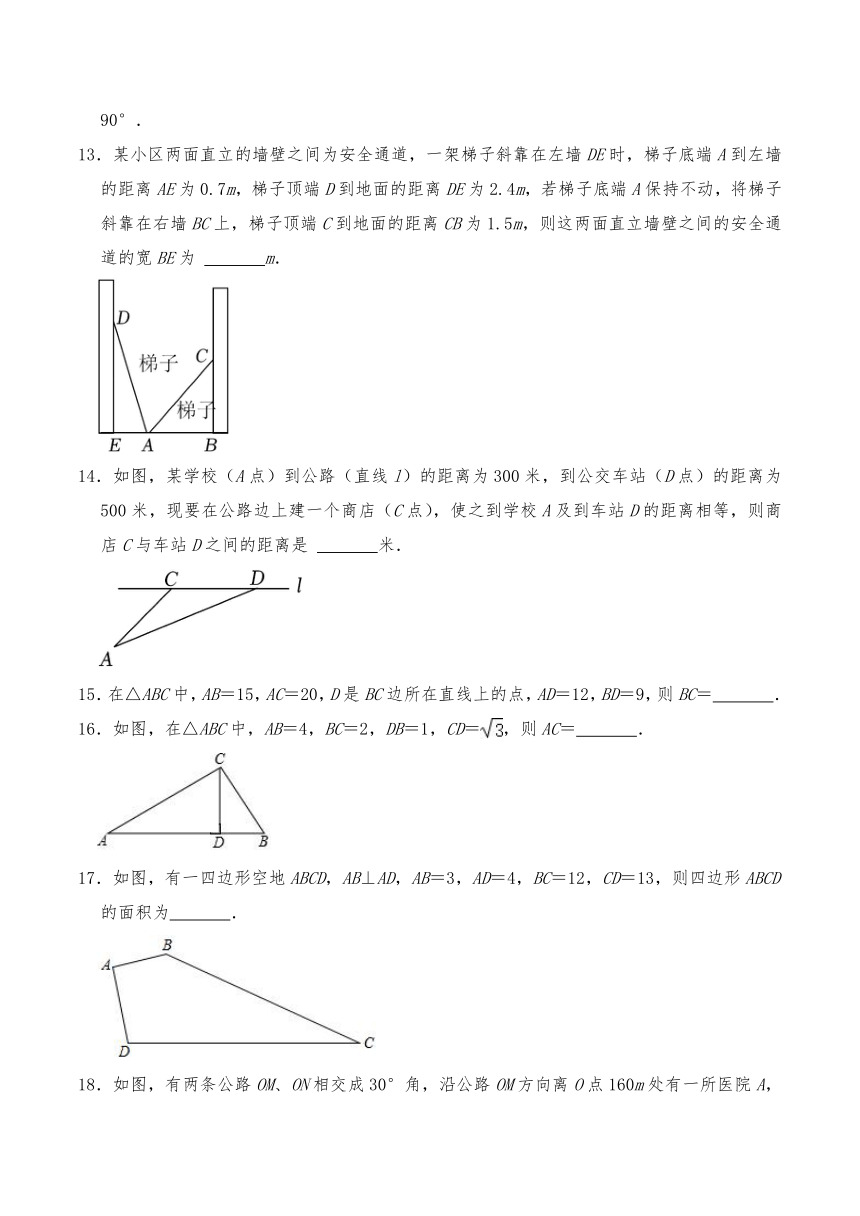
13.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全通道的宽BE为 m.
14.如图,某学校(A点)到公路(直线l)的距离为300米,到公交车站(D点)的距离为500米,现要在公路边上建一个商店(C点),使之到学校A及到车站D的距离相等,则商店C与车站D之间的距离是 米.
15.在△ABC中,AB=15,AC=20,D是BC边所在直线上的点,AD=12,BD=9,则BC= .
16.如图,在△ABC中,AB=4,BC=2,DB=1,CD=,则AC= .
17.如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为 .
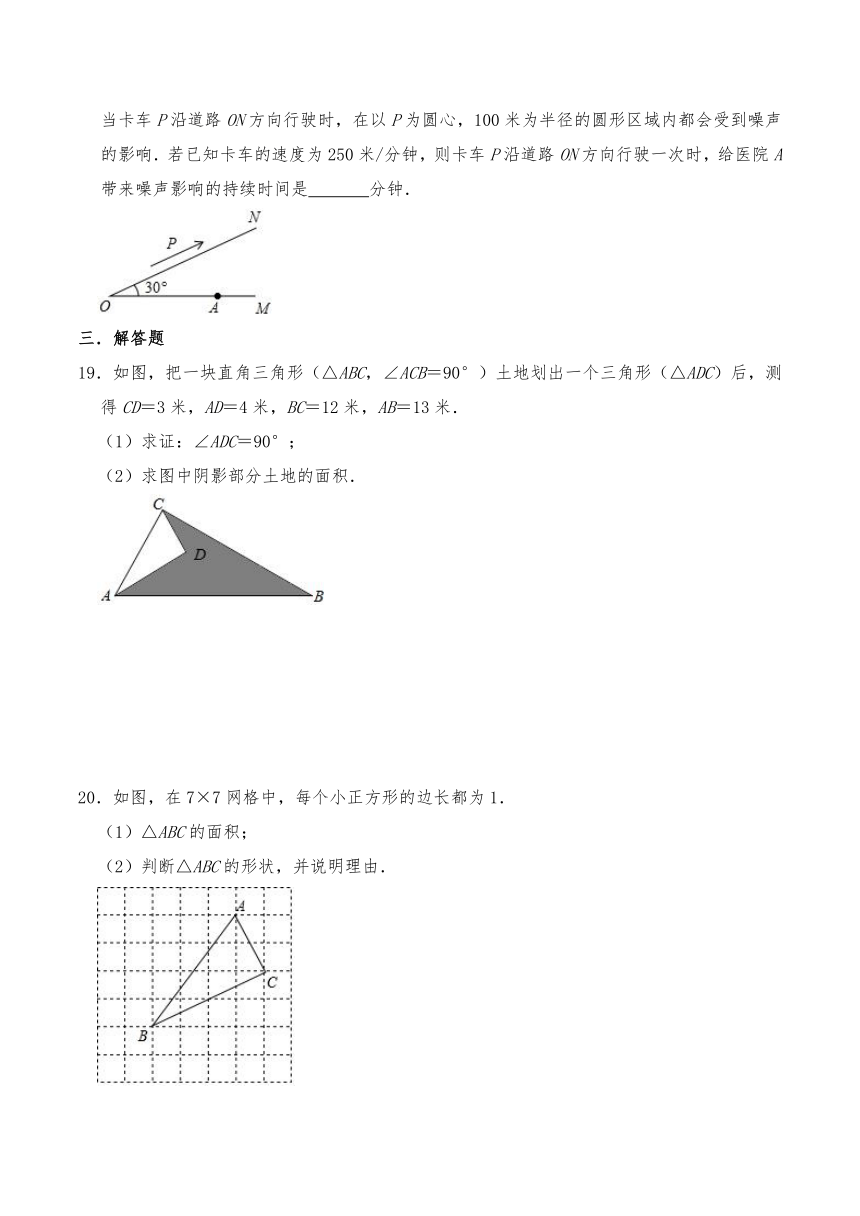
18.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点160m处有一所医院A,当卡车P沿道路ON方向行驶时,在以P为圆心,100米为半径的圆形区域内都会受到噪声的影响.若已知卡车的速度为250米/分钟,则卡车P沿道路ON方向行驶一次时,给医院A带来噪声影响的持续时间是 分钟.
三.解答题
19.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
20.如图,在7×7网格中,每个小正方形的边长都为1.
(1)△ABC的面积;
(2)判断△ABC的形状,并说明理由.
21.如图,有一块四边形的绿地ABCD,已知:AB=3m,BC=4m,∠B=90°,CD=12m,AD=13m.
(1)判断△ACD的形状;
(2)求这块绿地ABCD的面积.
22.小红同学与小颖同学相约在公园一角相距200m放风筝.已知小红的风筝线和水平线成30°,小颖的风筝线和水平线成45°,在某一时刻他们风筝正好在空中相遇(如图所示),求风筝的高度.即在△ABC中,∠ABC=30°,∠ACB=45°,AD⊥BC,D为垂足,BC=200m,求AD.
23.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
24.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
答案
一、选择题
D.A.C.A.C.D.B.B.B.C.
二.填空题
11.45°.12.直角、BAC. 13.2.7. 14.312.5.
15.25或7. 16.2. 17.36. 18.0.48.
三.解答题
19.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
20.(1)S△ABC=4×4﹣×4×2﹣×3×4﹣×1×2=5,
(2)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
21.(1)∵∠B=90°,
在直角△ABC中,由勾股定理得:AC===5(m),
∵52+122=132,
∴AC2+CD2=AD2,
∴△ACD是直角三角形;
(2)∵S四边形ABCD=S△ABC+S△ACD=AB BC+AC CD,
∴S四边形ABCD=×3×4+×5×12=6+30=36(m2),
答:该绿地ABCD的面积为36m2.
22.设AD=xcm,在Rt△ADC中,∠ACB=45°,
∴CD=x,BD=200﹣x,
在Rt△ADB中,∠ABC=30°,tanB=,
即tan30°=,
,
解得:x=100(﹣1)米,
答:AD约为100(﹣1)米.
23.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
24.(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
一、选择题
1.以下列各组数为边长能组成直角三角形的是( )
A.2、3、4 B.、、 C.32、42、52 D.6、8、10
2.下列几组数中,不能作为直角三角形的三边长的是( )
A.4,9,11 B.6,8,10 C.7,24,25 D.8,15,17
3.下列不能判定△ABC是直角三角形的是( )
A.a2+b2﹣c2=0 B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5 D.∠A+∠B=∠C
4.若△ABC中,AB=c,AC=b,BC=a,下列不能判定△ABC为直角三角形的是( )
A.a=32,b=42,c=52 B.a:b:c=5:12:13
C.(c+b)(c﹣b)=a2 D.∠A+∠B=∠C
5.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
6.如图,一棵大树在离地面3m,5m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部6m处,则大树折断前的高度是( )
A.9m B.14m C.11m D.10m
7.在△ABC中,若AC2﹣BC2=AB2,则( )
A.∠A=90° B.∠B=90° C.∠C=90° D.不能确定
8.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果∠A﹣∠B=∠C,那么△ABC是直角三角形
B.如果a2=b2﹣c2,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形
D.如果a2:b2:c2=9:16:25,那么△ABC是直角三角形
9.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
10.如图,要使宽为2米的矩形平板车ABCD通过宽为2米的等宽的直角通道,则平板车的长最多为( )
A.2 B.2 C.4 D.4
二.填空题
11.如图中的每个小方格都是边长为1的正方形,那么∠ABC的度数是 .
12.在△ABC中,如果AB=m2﹣n2,AC=2mn,BC=m2+n2,则△ABC是 三角形,其中∠ =90°.
13.某小区两面直立的墙壁之间为安全通道,一架梯子斜靠在左墙DE时,梯子底端A到左墙的距离AE为0.7m,梯子顶端D到地面的距离DE为2.4m,若梯子底端A保持不动,将梯子斜靠在右墙BC上,梯子顶端C到地面的距离CB为1.5m,则这两面直立墙壁之间的安全通道的宽BE为 m.
14.如图,某学校(A点)到公路(直线l)的距离为300米,到公交车站(D点)的距离为500米,现要在公路边上建一个商店(C点),使之到学校A及到车站D的距离相等,则商店C与车站D之间的距离是 米.
15.在△ABC中,AB=15,AC=20,D是BC边所在直线上的点,AD=12,BD=9,则BC= .
16.如图,在△ABC中,AB=4,BC=2,DB=1,CD=,则AC= .
17.如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为 .
18.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点160m处有一所医院A,当卡车P沿道路ON方向行驶时,在以P为圆心,100米为半径的圆形区域内都会受到噪声的影响.若已知卡车的速度为250米/分钟,则卡车P沿道路ON方向行驶一次时,给医院A带来噪声影响的持续时间是 分钟.
三.解答题
19.如图,把一块直角三角形(△ABC,∠ACB=90°)土地划出一个三角形(△ADC)后,测得CD=3米,AD=4米,BC=12米,AB=13米.
(1)求证:∠ADC=90°;
(2)求图中阴影部分土地的面积.
20.如图,在7×7网格中,每个小正方形的边长都为1.
(1)△ABC的面积;
(2)判断△ABC的形状,并说明理由.
21.如图,有一块四边形的绿地ABCD,已知:AB=3m,BC=4m,∠B=90°,CD=12m,AD=13m.
(1)判断△ACD的形状;
(2)求这块绿地ABCD的面积.
22.小红同学与小颖同学相约在公园一角相距200m放风筝.已知小红的风筝线和水平线成30°,小颖的风筝线和水平线成45°,在某一时刻他们风筝正好在空中相遇(如图所示),求风筝的高度.即在△ABC中,∠ABC=30°,∠ACB=45°,AD⊥BC,D为垂足,BC=200m,求AD.
23.如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC,DB,且CD=4,BD=3.
(1)求BC的长;
(2)求证:△BCD是直角三角形.
24.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
答案
一、选择题
D.A.C.A.C.D.B.B.B.C.
二.填空题
11.45°.12.直角、BAC. 13.2.7. 14.312.5.
15.25或7. 16.2. 17.36. 18.0.48.
三.解答题
19.(1)证明:∵∠ACB=90°,BC=12米,AB=13米,
∴AC===5(米),
∵CD=3米,AD=4米,
∴AD2+CD2=AC2=25,
∴∠ADC=90°;
(2)解:图中阴影部分土地的面积=A×BC﹣AD×CD=×5×12﹣×4×3=24(平方米).
20.(1)S△ABC=4×4﹣×4×2﹣×3×4﹣×1×2=5,
(2)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
21.(1)∵∠B=90°,
在直角△ABC中,由勾股定理得:AC===5(m),
∵52+122=132,
∴AC2+CD2=AD2,
∴△ACD是直角三角形;
(2)∵S四边形ABCD=S△ABC+S△ACD=AB BC+AC CD,
∴S四边形ABCD=×3×4+×5×12=6+30=36(m2),
答:该绿地ABCD的面积为36m2.
22.设AD=xcm,在Rt△ADC中,∠ACB=45°,
∴CD=x,BD=200﹣x,
在Rt△ADB中,∠ABC=30°,tanB=,
即tan30°=,
,
解得:x=100(﹣1)米,
答:AD约为100(﹣1)米.
23.(1)解:∵Rt△ABC中,∠BCA=90°,AC=12,AB=13,
∴BC===5;
(2)证明:∵在△BCD中,CD=4,BD=3,BC=5,
∴CD2+BD2=42+32=52=BC2,
∴△BCD是直角三角形.
24.(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
