沪科版八年级数学下册 19.1多边形内角和 试题(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 19.1多边形内角和 试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 388.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 15:01:14 | ||
图片预览

文档简介
19.1多边形内角和
一、选择题
1.若正多边形的内角和是,则该正多边形的一个外角为
A. B. C. D.
2.若边形的每个内角都与其外角相等,则的值为
A.3 B.4 C.6 D.8
3.一个正多边形的外角与其相邻的内角之比为,那么这个多边形的边数为
A.8 B.9 C.10 D.12
4.一个多边形截去一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是
A.10或11 B.11或12或13 C.11或12 D.10或11或12
5.下列哪个度数不可能是一个多边形的内角和
A. B. C. D.
6.如图所示,
A. B. C. D.
7.若一个多边形的每个外角都等于,则这个多边形是
A.四边形 B.七边形 C.六边形 D.五边形
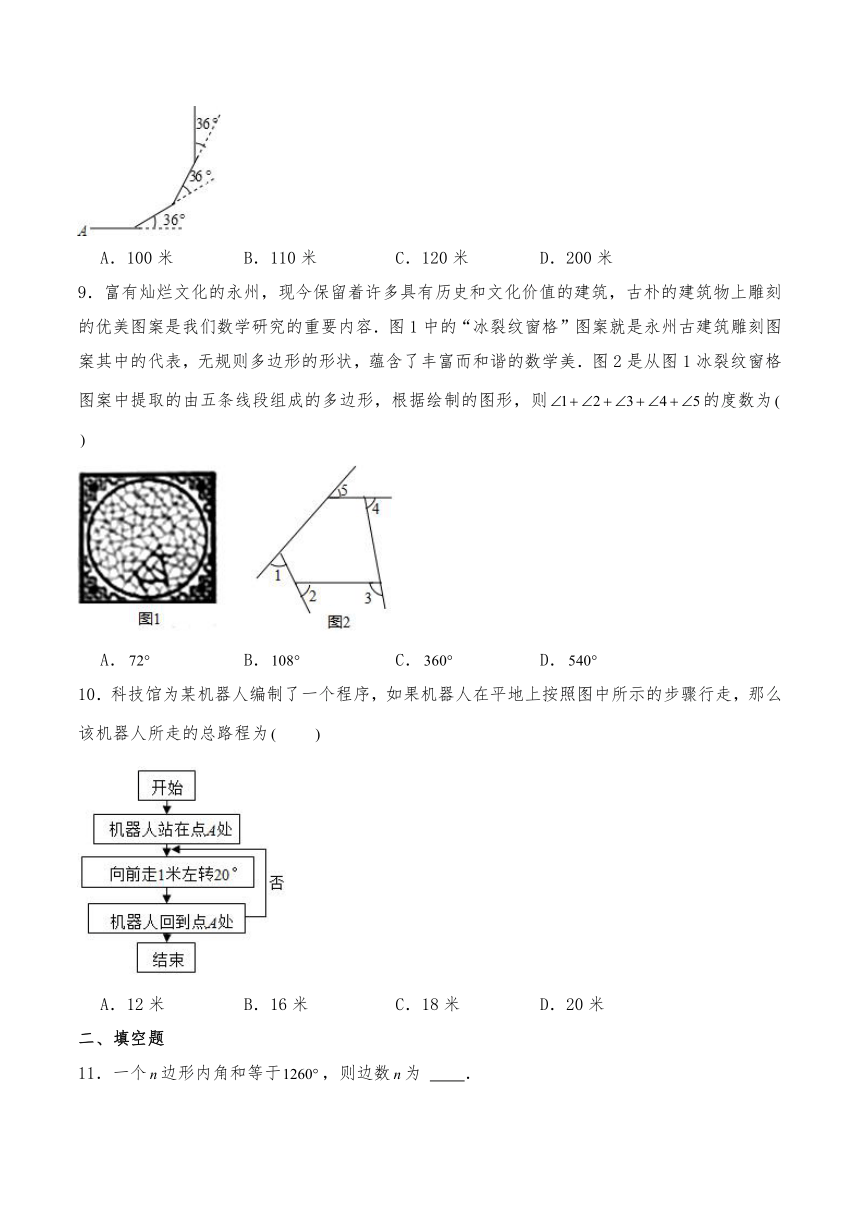
8.如图,小明从点出发,沿直线前进10米后向左转,再沿直线前进10米,再向左转照这样走下去,他第一次回到出发点点时,一共走的路程是
A.100米 B.110米 C.120米 D.200米
9.富有灿烂文化的永州,现今保留着许多具有历史和文化价值的建筑,古朴的建筑物上雕刻的优美图案是我们数学研究的重要内容.图1中的“冰裂纹窗格”图案就是永州古建筑雕刻图案其中的代表,无规则多边形的形状,蕴含了丰富而和谐的数学美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的多边形,根据绘制的图形,则的度数为
A. B. C. D.
10.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为
A.12米 B.16米 C.18米 D.20米
二、填空题
11.一个边形内角和等于,则边数为 .
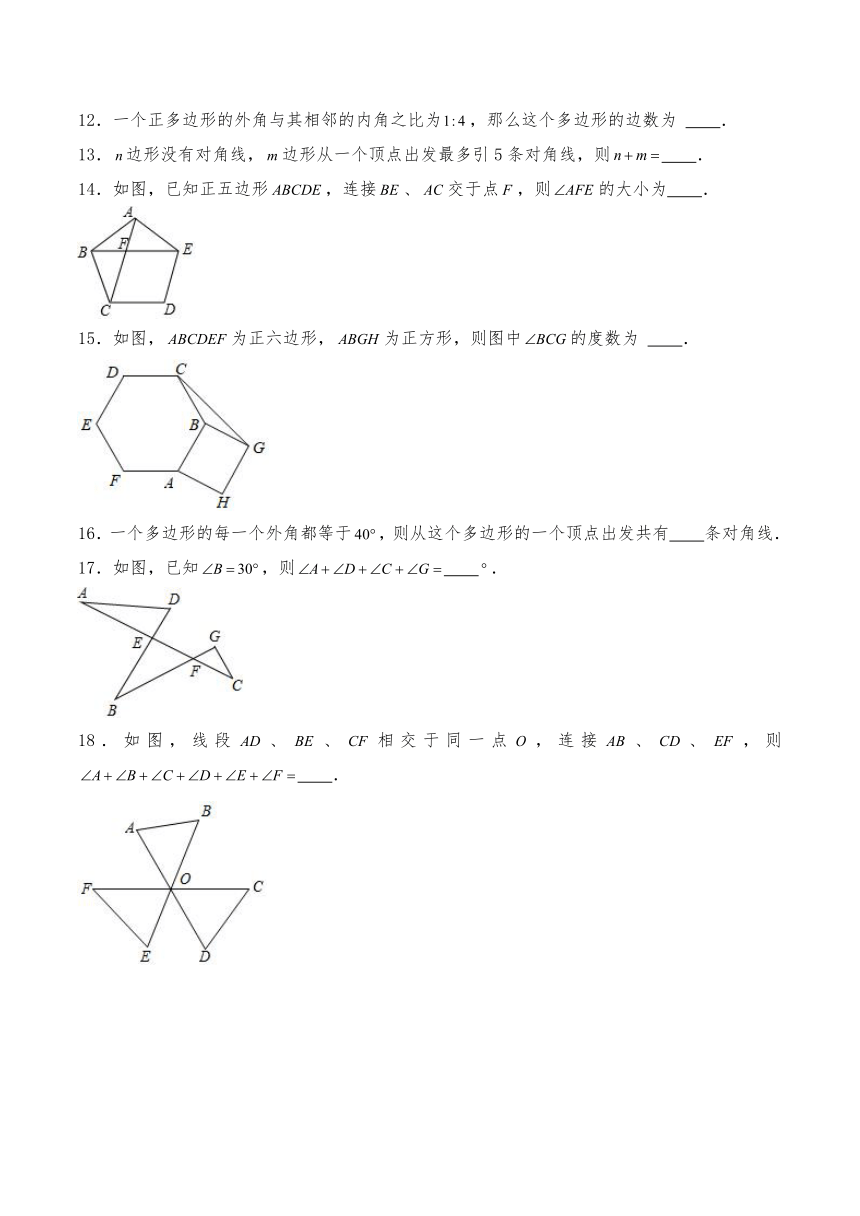
12.一个正多边形的外角与其相邻的内角之比为,那么这个多边形的边数为 .
13.边形没有对角线,边形从一个顶点出发最多引5条对角线,则 .
14.如图,已知正五边形,连接、交于点,则的大小为 .
15.如图,为正六边形,为正方形,则图中的度数为 .
16.一个多边形的每一个外角都等于,则从这个多边形的一个顶点出发共有 条对角线.
17.如图,已知,则 .
18.如图,线段、、相交于同一点,连接、、,则 .
三、解答题
19.计算:如图所示,求下列各图中的.
20.一个多边形的内角和比它的外角和的3倍少,求这个多边形的边数和内角和.
21.如图,将六边形纸片沿虚线剪去一个角后,得到.
(1)求六边形的内角和;
(2)求的度数.
22.(1)求12边形内角和度数;
(2)若一个边形的内角和与外角和的差是,求.
23.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
(2)根据规律,计算正八边形中的的度数;
(3)是否存在正边形使得?若存在,请求出的值,若不存在,请说明理由.
答案
一、选择题
..........
二.填空题
11.9. 12.十. 13.11. 14..
15.. 16.6. 17.210. 18..
三.解答题
19.(1)根据题意,得,
解得;
(2)根据题意,得,
解得,
又由得.
20.设这个多边形的边数为,
根据题意,得,
解得.
所以这个多边形的内角和为:.
21.(1)六边形的内角和为:;
(2)六边形的内角和为,,
,
.
即的度数是.
22.(1)由题意,得
;
(2)由题意得:
,
解得:.
23.(1)设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和;
当截线为只经过多边形一组邻边的一条直线时,多边形的边数增加一条边,内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
24.(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
(2)根据规律,计算正八边形中的;
(3)不存在,理由如下:
设存在正边形使得,
得.
解得,是正整数,(不符合题意要舍去),
不存在正边形使得.
一、选择题
1.若正多边形的内角和是,则该正多边形的一个外角为
A. B. C. D.
2.若边形的每个内角都与其外角相等,则的值为
A.3 B.4 C.6 D.8
3.一个正多边形的外角与其相邻的内角之比为,那么这个多边形的边数为
A.8 B.9 C.10 D.12
4.一个多边形截去一个角后,形成的另一个多边形的内角和是,则原来多边形的边数是
A.10或11 B.11或12或13 C.11或12 D.10或11或12
5.下列哪个度数不可能是一个多边形的内角和
A. B. C. D.
6.如图所示,
A. B. C. D.
7.若一个多边形的每个外角都等于,则这个多边形是
A.四边形 B.七边形 C.六边形 D.五边形
8.如图,小明从点出发,沿直线前进10米后向左转,再沿直线前进10米,再向左转照这样走下去,他第一次回到出发点点时,一共走的路程是
A.100米 B.110米 C.120米 D.200米
9.富有灿烂文化的永州,现今保留着许多具有历史和文化价值的建筑,古朴的建筑物上雕刻的优美图案是我们数学研究的重要内容.图1中的“冰裂纹窗格”图案就是永州古建筑雕刻图案其中的代表,无规则多边形的形状,蕴含了丰富而和谐的数学美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的多边形,根据绘制的图形,则的度数为
A. B. C. D.
10.科技馆为某机器人编制了一个程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为
A.12米 B.16米 C.18米 D.20米
二、填空题
11.一个边形内角和等于,则边数为 .
12.一个正多边形的外角与其相邻的内角之比为,那么这个多边形的边数为 .
13.边形没有对角线,边形从一个顶点出发最多引5条对角线,则 .
14.如图,已知正五边形,连接、交于点,则的大小为 .
15.如图,为正六边形,为正方形,则图中的度数为 .
16.一个多边形的每一个外角都等于,则从这个多边形的一个顶点出发共有 条对角线.
17.如图,已知,则 .
18.如图,线段、、相交于同一点,连接、、,则 .
三、解答题
19.计算:如图所示,求下列各图中的.
20.一个多边形的内角和比它的外角和的3倍少,求这个多边形的边数和内角和.
21.如图,将六边形纸片沿虚线剪去一个角后,得到.
(1)求六边形的内角和;
(2)求的度数.
22.(1)求12边形内角和度数;
(2)若一个边形的内角和与外角和的差是,求.
23.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
24.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
(2)根据规律,计算正八边形中的的度数;
(3)是否存在正边形使得?若存在,请求出的值,若不存在,请说明理由.
答案
一、选择题
..........
二.填空题
11.9. 12.十. 13.11. 14..
15.. 16.6. 17.210. 18..
三.解答题
19.(1)根据题意,得,
解得;
(2)根据题意,得,
解得,
又由得.
20.设这个多边形的边数为,
根据题意,得,
解得.
所以这个多边形的内角和为:.
21.(1)六边形的内角和为:;
(2)六边形的内角和为,,
,
.
即的度数是.
22.(1)由题意,得
;
(2)由题意得:
,
解得:.
23.(1)设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和;
当截线为只经过多边形一组邻边的一条直线时,多边形的边数增加一条边,内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
24.(1)观察上面每个正多边形中的,填写下表:
正多边形边数 3 4 5 6
的度数
(2)根据规律,计算正八边形中的;
(3)不存在,理由如下:
设存在正边形使得,
得.
解得,是正整数,(不符合题意要舍去),
不存在正边形使得.
